Лекция
Привет, сегодня поговорим про метод наименьших квадратов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое метод наименьших квадратов , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
До начала XIX в. ученые не имели определенных правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приемы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés) . Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения . Метод распространен и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Работы А. А. Маркова в начале XX века позволили включить метод наименьших квадратов в теорию оценивания математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф.Дэвида, А. Эйткена, С. Рао было получено немало важных результатов в этой области .
Пусть 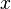 — набор
— набор  неизвестных переменных (параметров),
неизвестных переменных (параметров), 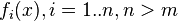 — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым значениям
— совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым значениям 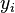 . По существу речь идет о «решении» переопределенной системы уравнений
. По существу речь идет о «решении» переопределенной системы уравнений  в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей —
в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей — 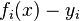 . Таким образом, сущность МНК может быть выражена следующим образом:
. Таким образом, сущность МНК может быть выражена следующим образом:
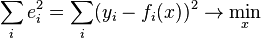
В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор 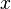 в смысле максимальной близости векторов
в смысле максимальной близости векторов  и
и  или максимальной близости вектора отклонений
или максимальной близости вектора отклонений  к нулю (близость понимается в смысле евклидова расстояния).
к нулю (близость понимается в смысле евклидова расстояния).
В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений
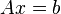 ,
,
где матрица 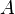 не квадратная, а прямоугольная размера
не квадратная, а прямоугольная размера  (точнее ранг матрицы A больше количества искомых переменных).
(точнее ранг матрицы A больше количества искомых переменных).
Такая система уравнений, в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора 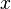 , чтобы минимизировать «расстояние» между векторами
, чтобы минимизировать «расстояние» между векторами 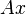 и
и 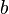 . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть
. Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть  . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
. Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
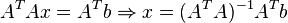
Используя оператор псевдоинверсии, решение можно переписать так:
 ,
,
где 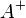 — псевдообратная матрица для
— псевдообратная матрица для 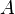 .
.
Данную задачу также можно «решить» используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
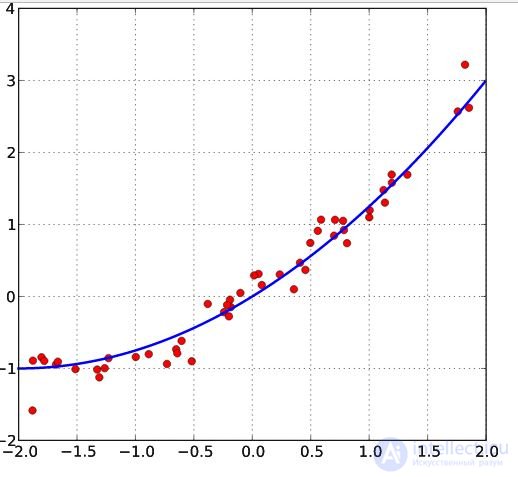
Пусть имеется 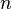 значений некоторой переменной
значений некоторой переменной  (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных
(это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных 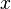 . Задача заключается в том, чтобы взаимосвязь между
. Задача заключается в том, чтобы взаимосвязь между  и
и 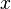 аппроксимировать некоторой функцией
аппроксимировать некоторой функцией  , известной с точностью до некоторых неизвестных параметров
, известной с точностью до некоторых неизвестных параметров 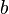 , то есть фактически найти наилучшие значения параметров
, то есть фактически найти наилучшие значения параметров 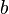 , максимально приближающие значения
, максимально приближающие значения  к фактическим значениям
к фактическим значениям  . Об этом говорит сайт https://intellect.icu . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно
. Об этом говорит сайт https://intellect.icu . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно 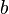 :
:
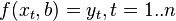
В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными
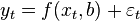
где  — так называемые случайные ошибки модели.
— так называемые случайные ошибки модели.
Соответственно, отклонения наблюдаемых значений  от модельных
от модельных  предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры
предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры 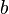 , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии)
, при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии)  будет минимальной:
будет минимальной:

где  — англ. Residual Sum of Squares определяется как:
— англ. Residual Sum of Squares определяется как:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции  , продифференцировав ее по неизвестным параметрам
, продифференцировав ее по неизвестным параметрам 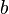 , приравняв производные к нулю и решив полученную систему уравнений:
, приравняв производные к нулю и решив полученную систему уравнений:
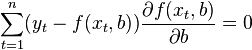
Пусть регрессионная зависимость является линейной:

Пусть y — вектор-столбец наблюдений объясняемой переменной, а  — это
— это  -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
-матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
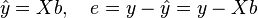
соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров 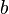 и приравняв производные к нулю, получим систему уравнений (в матричной форме):
и приравняв производные к нулю, получим систему уравнений (в матричной форме):
 .
.
В расшифрованной матричной форме эта система уравнений выглядит следующим образом:
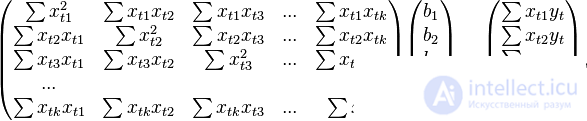 где все суммы берутся по всем допустимым значениям
где все суммы берутся по всем допустимым значениям 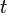 .
.
Если в модель включена константа (как обычно), то 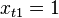 при всех
при всех 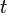 , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений
, поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений 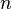 , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных:
, а в остальных элементах первой строки и первого столбца — просто суммы значений переменных:  и первый элемент правой части системы —
и первый элемент правой части системы — 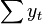 .
.
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
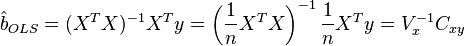
Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные еще и нормированы на СКО (то есть в конечном итогестандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
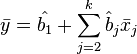
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое , известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от нее.
В случае парной линейной регрессии  , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:
, когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

Отсюда несложно найти оценки коэффициентов:

Несмотря на то что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа  должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид
должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид 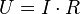 ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идет о модели
; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идет о модели  . В этом случае вместо системы уравнений имеем единственное уравнение
. В этом случае вместо системы уравнений имеем единственное уравнение
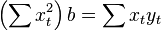
Следовательно, формула оценки единственного коэффициента имеет вид
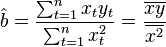
В первую очередь , отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведенной формулы. Длянесмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожиданиеслучайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
Первое условие можно считать выполненным всегда для моделей с константой, так как константа берет на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объем данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы  к некоторой невырожденной матрице при увеличении объема выборки до бесконечности.
к некоторой невырожденной матрице при увеличении объема выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были еще и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
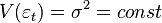
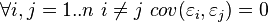
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок 
Линейная модель , удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещенными,состоятельными и наиболее эффективными оценками в классе всех линейных несмещенных оценок (в англоязычной литературе иногда употребляют аббревиатуруBLUE (Best Linear Unbiased Estimator) — наилучшая линейная несмещенная оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещенной и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
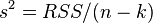
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещеннымии состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясьнесмещенными и состоятельными). Однако, еще более ухудшается оценка ковариационной матрицы — она становится смещенной и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщенного МНК.
Метод наименьших квадратов допускает широкое обобщение . Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков 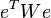 , где
, где  — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение
— некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение 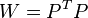 . Следовательно, указанный функционал можно представить следующим образом
. Следовательно, указанный функционал можно представить следующим образом 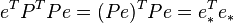 , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
, то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано ( теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок:  .
.
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
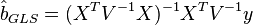
Ковариационная матрица этих оценок соответственно будет равна
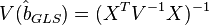
Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели , то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: 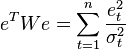 . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
. Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
На этом все! Теперь вы знаете все про метод наименьших квадратов, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое метод наименьших квадратов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ