Таблица основных производящих функций и доказательство (вывод). кратко

Лекция

Привет, сегодня поговорим про таблица производящих функций, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое таблица производящих функций , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

таблица производящих функций

В таблице указаны основные производящие функции, которые обычно требуются для решения типичных задач. Все суммы ∑ выполняются по переменной n от 0 до ∞, если не указано иное. Элементы последовательности нумеруются от 0.

$\begin{displaymath} \begin{tabular}{\vert r\vert l\vert l\vert l\vert} \hlin... ...$\displaystyle e^z$ \\ & & & \\ \hline \end{tabular} \end{displaymath}$

ДОКАЗАТЕЛЬСТВО

Предлагаемые для рассмотрения производящие функции являются своего рода «азбукой», или, если угодно, «таблицей умножения» для теории производящий функций. Понимание этих производящих функций позволит работать с более сложными выражениями, а знание таблицы ускорит многие устные вычисления.

Первая и вторая производящие функции выводятся непосредственно из определения (см. «Введение»). Третья последовательность подробно разбирается в приложении «О разложении 1/(1−z)».

Производящая функция последовательности №4 получается заменой z на −z в функции для последовательности №3. Аналогично получаются производящие функции для последовательностей №5, №7 и №8: нужно заменить в третьей производящей функии z наz^m, 2z и rz соответственно.

Производящая функция последовательности №6 получается путем дифференцирования функции №3:

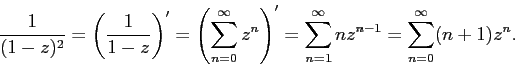
$\begin{displaymath} \frac{1}{(1-z)^2}=\left(\frac{1}{1-z}\right)'=\left(\sum_{... ...m_{n=1}^{\infty} nz^{n-1}= \sum_{n=0}^{\infty} (n+1)z^{n}. \end{displaymath}$

Точно такой же результат получается, если использовать биномиальный ряд (см. Об этом говорит сайт https://intellect.icu . «Расширенные биномиальные коэффициенты»):

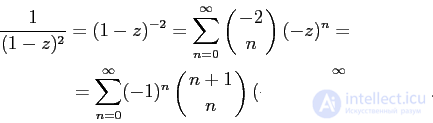
$\begin{displaymath}\displaylines{ \ig{0.3}\frac{1}{(1-z)^2}=(1-z)^{-2}=\sum_{n... ...{n+1}{n}(-z)^{n}=\sum_{n=0}^{\infty} (n+1)z^{n}.\ig{0.3} } \end{displaymath}$

Совершенно аналогично нужно поступить с производящей функцией последовательностей №10 и №11:

$\begin{displaymath} \frac{1}{(1-z)^m}=(1-z)^{-m}=\sum_{n=0}^{\infty}\binom{m+n-1}{n}z^{n} \quad \mbox{(это \no10)}, \end{displaymath}$

если теперь заменить m на m+1 и использовать тот факт, что для целых положительных nсправедливо тождество 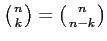Таблица основных производящих функций и доказательство (вывод). , то получим одиннадцатую строку таблицы:

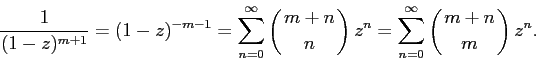
$\begin{displaymath} \frac{1}{(1-z)^{m+1}}=(1-z)^{-m-1}=\sum_{n=0}^{\infty}\binom{m+n}{n}z^{n}=\sum_{n=0}^{\infty}\binom{m+n}{m}z^{n}. \end{displaymath}$

Последовательность №9 и производящая функция для нее следуют из биномиальной теоремы (после замены a на z, а b на 1 ), утверждение которой доказывается в курсе комбинаторики:

$\begin{displaymath} (a+b)^m = \sum_{n=0}^{m}\binom{m}{n} a^nb^{m-n}, \quad m\geq 0, \mbox{ целое}. \end{displaymath}$

Производящая функция для последовательности №12 получается интегрированием производящей функции для последовательности №3 (полагаем, что константа интегрирования равна нулю, чтобы выполнялось a₀=0):

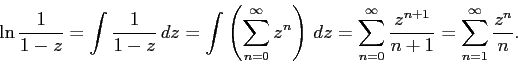
$\begin{displaymath} \ln\frac1{1-z}=\int \frac1{1-z} dz=\int\left(\sum_{n=0}^{... ... \frac{z^{n+1}}{n+1}= \sum_{n=1}^{\infty} \frac{z^{n}}{n}. \end{displaymath}$

Последовательность №13 получается аналогично, но c дополнительной заменой z на −zи умножением результата на −1.

Разложение в ряд экспоненты (строка №14 таблицы) известно из курса математического анализа. По формуле Тейлора коэффициент при zⁿ равен производной порядка n, вычисленной в нуле, поделенной на n!:

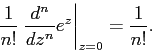
$\begin{displaymath} \frac{1}{n!}\left.\frac{d^n}{dz^n} e^z \right\vert _{z=0} = \frac{1}{n!}. \end{displaymath}$

Причем ряд для экспоненты сходится для любого комплексного z (если, конечно, считать, что z — число).

Cм. также

Надеюсь, эта статья про таблица производящих функций, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое таблица производящих функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про таблица производящих функций

Таблица основных производящих функций и доказательство (вывод). кратко

таблица производящих функций

ДОКАЗАТЕЛЬСТВО

Cм. также

Комментарии

Оставить комментарий

Теория вероятностей. Математическая статистика и Стохастический анализ

Термины: Теория вероятностей. Математическая статистика и Стохастический анализ