Лекция
Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы.
математическая статистика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
Во многих своих разделах математическая статистика опирается на теорию вероятностей, дающую возможность оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании).
До сих пор, говоря о законах распределения случайных величин, мы не затрагивали вопроса о том, откуда берутся, на каком основании устанавливаются эти законы распределения. Ответ на вопрос вполне определенен – в основе всех этих характеристик лежит опыт; каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные. Оперируя такими понятиями, как события и их вероятности, случайные величины, их законы распределения и числовые характеристики, теория вероятностей дает возможность теоретическим путем определять вероятности одних событий через вероятности других, законы распределения и числовые характеристики одних случайных величин через законы распределения и числовые характеристики других. Такие косвенные методы позволяют значительно экономить время и средства, затрачиваемые на эксперимент, но отнюдь не исключают самого эксперимента. Каждое исследование в области случайных явлений, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений.
Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специальной науки – математической статистики.
Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму.
Охарактеризуем вкратце некоторые типичные задачи математической статистики, часто встречаемые на практике.
Мы уже указывали, что закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат больший или меньший элемент случайности. Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности, сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникает характерная для математической статистики задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.
Эта задача тесно связана с предыдущей; при решении такого рода задач мы обычно не располагаем настолько обширным статистическим материалом, чтобы выявляющиеся в нем статистические закономерности были в достаточной мере свободны от элементов случайности. Статистический материал может с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы. Например, может возникнуть такой вопрос: согласуются ли результаты эксперимента с гипотезой о том, что данная случайная величина подчинена закону распределения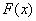 
? Другой подобный вопрос: указывает ли наблюденная в опыте тенденция к зависимости между двумя случайными величинами на наличие действительной объективной зависимости между ними или же она объясняется случайными причинами, связанными с недостаточным объемом наблюдений? Для решения подобных вопросов математическая статистика выработала ряд специальных приемов.
Часто при обработке статистического материала вовсе не возникает вопрос об определении законов распределения исследуемых случайных величин. Обыкновенно это бывает связано с крайне недостаточным объемом экспериментального материала. Иногда же характер закона распределения качественно известен до опыта, из теоретических соображений; например, часто можно утверждать заранее, что случайная величина подчинена нормальному закону. Тогда возникает более узкая задача обработки наблюдений – определить только некоторые параметры (числовые характеристики) случайной величины или системы случайных величин. При небольшом числе опытов задача более или менее точного определения этих параметров е может быть решена; в этих случаях экспериментальный материал содержит в себе неизбежно значительный элемент случайности; поэтому случайными оказываются и все параметры, вычисленные на основе этих данных. В таких условиях может быть поставлена только задача об определении так называемых «оценок» или «подходящих значений» для искомых параметров, т.е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие. С задачей отыскания «подходящих значений» числовых характеристик тесно связана задача оценки их точности и надежности. С подобными задачами мы встретимся в главе 14.
Таков далеко не полный перечень основных задач математической статистики. Мы перечислили только те из них, которые наиболее важны для нас по своим практическим применениям. В настоящей главе мы вкратце познакомимся с некоторыми, наиболее элементарными задачами математической статистики и с методами их решения.
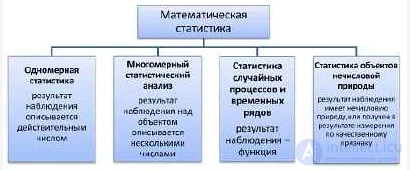
Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. В зависимости от математической природы конкретных результатов наблюдений, математическая статистика делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы.
Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез. Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики предполагают использование возможностей современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости.
Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используют точечные и интервальные оценки.
Большой раздел современной математической статистики — статистический последовательный анализ, фундаментальный вклад в создание и развитие которого внес А. Вальд во время Второй мировой войны. В отличие от традиционных (непоследовательных) методов статистического анализа, основанных на случайной выборке фиксированного объема, в последовательном анализе допускается формирование массива наблюдений по одному (или, более общим образом, группами), при этом решение о проведении следующего наблюдения (группы наблюдений) принимается на основе уже накопленного массива наблюдений. Ввиду этого, теория последовательного статистического анализа тесно связана с теорией оптимальной остановки.
В математической статистике есть общая теория проверки гипотез и большое число методов, посвященных проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и характеристик, о проверке однородности (то есть о совпадении характеристик или функций распределения в двух выборках), о согласии эмпирической функции распределения с заданной функцией распределения или с параметрическим семейством таких функций, о симметрии распределения и др.
Большое значение имеет раздел математической статистики, связанный с проведением выборочных обследований, со свойствами различных схем организации выборок и построением адекватных методов оценивания и проверки гипотез.
Задачи восстановления зависимостей активно изучаются более 200 лет, с момента разработки метода наименьших квадратов К. Гауссом, А.-М. Лежандром и Р. Эдрейном на рубеже XVIII и XIX веков.
Разработка методов аппроксимации данных и сокращения размерности описания была начата более 100 лет назад, когда Карл Пирсон создал метод главных компонент. Позднее были разработаны факторный анализ и многочисленные нелинейные обобщения.
Различные методы построения (кластер-анализ), анализа и использования (дискриминантный анализ) классификаций (типологий) именуют также методами распознавания образов (с учителем и без), автоматической классификации и др.
В настоящее время компьютеры играют большую роль в математической статистике. Они используются как для расчетов, так и для имитационного моделирования (в частности, в методах размножения выборок и при изучении пригодности асимптотических результатов).
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ