9.4. Вероятность попадания в эллипс рассеивания кратко

Привет, Вы узнаете о том , что такое вероятность попадания в эллипс рассеивания, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вероятность попадания в эллипс рассеивания , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

К числу немногих плоских фигур, вероятность попадания в которые может быть вычислена в конечном виде, принадлежит эллипс рассеивания (эллипс равной плотности).

 

Пусть нормальный закон на плоскости задан в канонической форме:

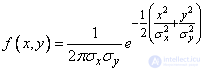.                                             (9.4.1)

Рассмотрим эллипс рассеивания 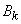, уравнение которого

,

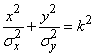где параметр 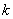 представляет собой отношение полуосей эллипса рассеивания к главным средним квадратическим отклонениям. По общей формуле (8.3.3) имеем:

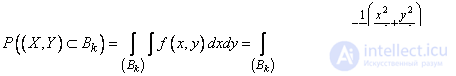.                 (9.4.2)

Сделаем в интеграле (9.4.2) замену переменных

.

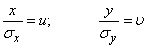Этой подстановкой эллипс 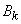 преобразуется в круг  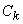радиуса 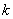. Следовательно,

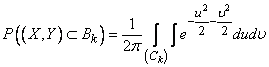.                            (9.4.3)

Перейдем в интеграле (9.4.3) от декартовой  системы  координат к полярной, положив

.                          (9.4.4)

Якобиан преобразования (9.4.4) равен 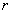. Производя замену переменных, получим:

.

Таким образом, вероятность попадания случайной точки в эллипс рассеивания, полуоси которого равны 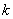 средним квадратическим отклонениям, равна:

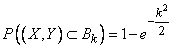.                             (9.4.5)

В качестве примера найдем вероятность попадания случайной точки, распределенной по нормальному закону на плоскости 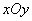 в единичный эллипс рассеивания, полуоси которого равны средним квадратическим отклонениям:

.

Для такого эллипса 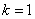. Имеем:

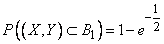
Пользуясь таблицей 2 приложения, находим:

.

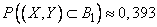Формула (9.4.5) чаще всего применяется для вычисления вероятности попадания в круг при круговом рассеивании.

Пример. На пути быстро движущейся малоразмерной цели площади 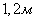 ставится осколочное поле в форме плоского диска радиуса 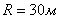. Об этом говорит сайт https://intellect.icu . Внутри диска плотность осколков постоянна и равна 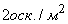. Если цель накрыта диском, то число осколков, попадающих в нее, можно считать распределенным по закону Пуассона. В силу малости цели можно рассматривать ее как точечную и считать, что она или полностью накрывается осколочным полем (если ее центр попадает в осколочный круг), или совсем не накрывается (если ее центр не попадает в круг). Попадание осколка гарантирует поражение цели. При прицеливании центр круга  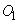стремятся совместить в плоскости  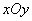с началом координат  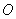(центром цели), но вследствие ошибок точка  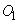рассеивается около  (рис. 9.4.1). Закон рассеивания нормальный, рассеивание круговое, 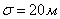. Определить вероятность поражения цели .

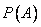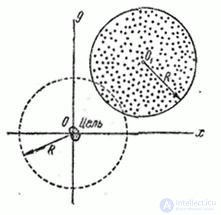
Рис. 9.4.1

Решение. Чтобы цель была поражена осколками, необходимо совмещение двух событий: 1) попадание цели (точки 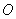) в осколочное поле (круг радиуса 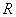) и 2) поражение цели при условии, что попадание произошло.

Вероятность попадания цели в круг, очевидно, равна вероятности того, что центр круга (случайная точка 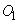) попадает в круг радиуса 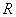, описанный вокруг начала координат. Применим формулу (9.4.5). Имеем:

.

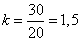Вероятность попадания цели в осколочное поле равна:

.

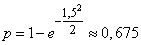Далее найдем вероятность поражения цели 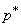 при условии, что она накрыта осколочным диском. Среднее число осколков 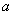, попадающих в накрытую полем цель, равно произведению площади цели на плотность поля осколков:

.

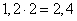Условная вероятность поражения цели 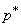есть не что иное, как вероятность попадания в нее хотя бы одного осколка. Пользуясь формулой (5.9.5) главы 5, имеем:

.

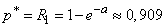Вероятность поражения цели равна:

.

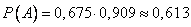Воспользуемся формулой (9.4.5) для вероятности попадания в круг, чтобы вывести одно важное для практики распределение: так называемое распределение Релея.

Рассмотрим на плоскости 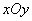 (рис. 9.4.2) случайную точку 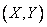, рассеивающуюся вокруг начала координат  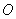по круговому нормальному закону со средним квадратическим отклонением 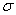. Найдем закон распределения случайной величины  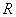- расстояния от точки  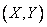до начала координат, т.е. длины случайного вектора с составляющими .

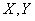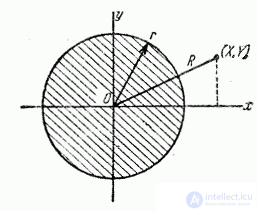
Рис. 9.4.2.

Найдем сначала функцию распределения 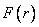 величины 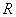. По определению

.

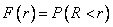Это есть не что иное, как вероятность попадания случайной точки 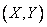 внутрь круга радиуса  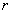(рис. 9.4.2). По формуле (9.4.5) эта вероятность равна:

,

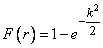где 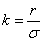, т.е.

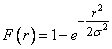.                                (9.4.6)

Данное выражение функции распределения имеет смысл только при положительных значениях 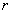; при отрицательных  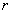нужно положить .

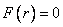Дифференцируя функцию распределения 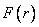 по 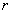, найдем плотность распределения

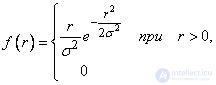                               (9.4.7)

Закон Релея (9.4.7) встречается в разных областях практика в стрельбе, радиотехнике, электротехнике и др.

График функции 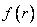 (плотности закона Релея) приведен на рис.9.4.3.

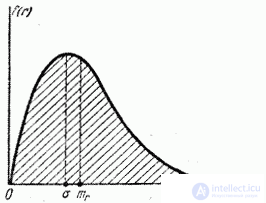
Рис. 9.4.3

Найдем числовые характеристики величины 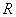, распределенной по закону Релея, а именно: ее моду  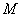и математическое ожидание 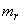. Для того чтобы найти моду – абсциссу точки, в которой плотность вероятности максимальна, продифференцируем  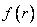и приравняем производную нулю:

.

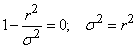Корень этого уравнения и есть искомая мода

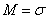.                                     (9.4.8)

Таким образом, наивероятнейшее значение расстояния 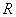 случайной точки  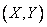от начала координат равно среднему квадратическому отклонению рассеивания.

Математическое ожидание 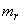 найдем по формуле

.

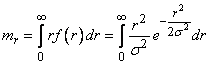Производя замену переменной

.

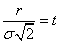получим:

.

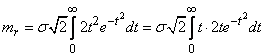Интегрируя по частям, найдем математическое ожидание расстояния :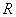

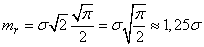.                                 (9.4.9)

 

Информация, изложенная в данной статье про вероятность попадания в эллипс рассеивания , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое вероятность попадания в эллипс рассеивания и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про вероятность попадания в эллипс рассеивания