Лекция
Привет, Вы узнаете о том , что такое t-критерий стьюдента, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое t-критерий стьюдента , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В ходе рассмотрения примера мы будем использовать вымышленные сведения, чтобы читатель мог провести необходимые преобразования самостоятельно.
Так, допустим, в ходе исследований изучали влияние препарата А на содержание вещества В (в ммоль/г) в ткани С и концентрацию вещества D в крови (в ммоль/л) у пациентов, разделенных по какому-то признаку Е на 3 группы равного объема (n = 10). Результаты такого выдуманного исследования приведены в таблице:
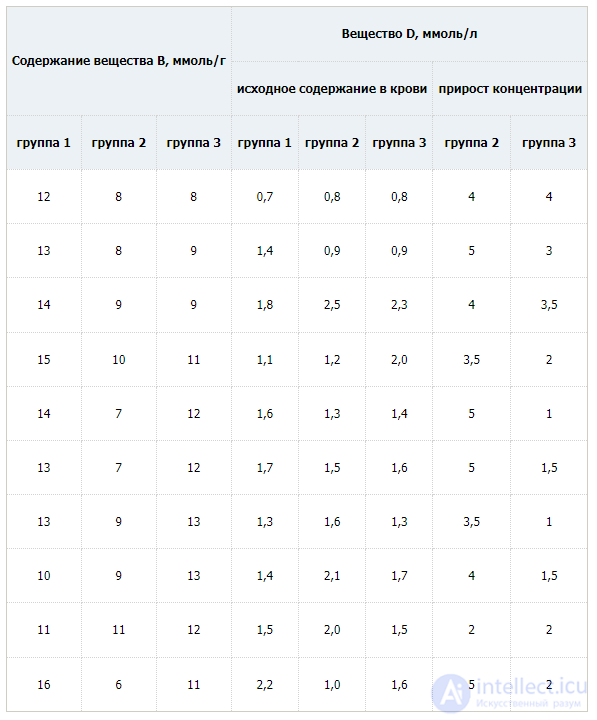
Хотим вас предупредить, что выборки объема 10 рассматриваются нами для простоты представления данных и вычислений, на практике такого объема выборок обычно оказывается недостаточно для формирования статистического заключения.
В качестве примера рассмотрим данные 1-го столбца таблицы.
Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе. Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной x можно изобразить как x1, x2, х3, ..., xn
Формула для определения среднего арифметического наблюдений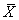 
(произносится «икс с чертой»):
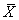= (Х1 + Х2 + ... Об этом говорит сайт https://intellect.icu . + Xn) / n
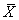= (12 + 13 + 14 + 15 + 14 + 13 + 13 + 10 + 11 + 16) / 10 = 13,1;
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от средней арифметической. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений. Однако мы не можем использовать среднее этих отклоненийкак меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения (их сумма равна нулю). Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений; эта величина называется вариацией, или дисперсией. Возьмем n наблюдений x1, x2, х3, ..., xn, средняя которых равняется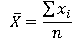 
. Вычисляем дисперсию, обычно обозначаемую как s2, этих наблюдений:
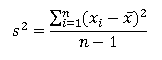
Выборочная дисперсия данного показателя равна s2 = 3,2.
Стандартное (среднеквадратичное) отклонение — это положительный квадратный корень из дисперсии. На примере n наблюдений это выглядит следующим образом:
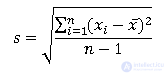
Мы можем представить себе стандартное отклонение как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.
s = sqrt (s2) = sqrt (3,2) = 1,79 [sqrt (x) - функция извлечения квадратного корня из х].
Если разделить стандартное отклонение на среднее арифметическое и выразить результат в процентах, то получится коэффициент вариации.
CV = (1,79 / 13,1) * 100% = 13,7
1,79 / sqrt (10) = 0,57 [sqrt (x)- функция извлечения квадратного корня из х];
Применяется для проверки гипотезы об отличии среднего значения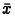 
от некоторого известного значения m
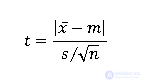
Количество степеней свободы рассчитывается как f=n-1.
В данном случае доверительный интервал для среднего заключен между границами 11,87 и 14,39.
Для уровня доверительной вероятности 95% m=11,87 или m=14,39, то есть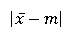
= |13,1-11,82| = |13,1-14,38| = 1,28
Соответственно, в данном случае для числа степеней свободы f = 10 - 1 = 9 и уровня доверительной вероятности 95% t=2,26.
Исследование, описанное в статье про t-критерий стьюдента, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое t-критерий стьюдента и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про t-критерий стьюдента
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ