Лекция
Привет, Вы узнаете о том , что такое нормальный закон в пространстве трех измерений , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое нормальный закон в пространстве трех измерений , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
При исследования вопросов, связанных со стрельбой дистанционными снарядами, приходится иметь дело с законом распределения точек разрыва дистанционного снаряда в пространстве. При условии применения обычных дистанционных взрывателей этот закон распределения может считаться нормальным.
В данном 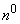 мы рассмотрим лишь каноническую форму нормального закона в пространстве:
мы рассмотрим лишь каноническую форму нормального закона в пространстве:
 , (9.6.1)
, (9.6.1)
где 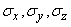 - главные средние квадратические отклонения.
- главные средние квадратические отклонения.
Переходя от средних квадратических отклонений к вероятным, имеем:
 . (9.6.2)
. (9.6.2)
При решении задач, связанных со стрельбой дистанционными снарядами, иногда приходится вычислять вероятность разрыва дистанционного снаряда в пределах заданной области 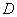 . В общем случае эта вероятность выряжается тройным интегралом:
. В общем случае эта вероятность выряжается тройным интегралом:
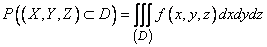 . (9.6.3)
. (9.6.3)
Интеграл (9.6.3) обычно не выражается через элементарные функции. Однако существует ряд областей, вероятность попадания в которые вычисляется сравнительно просто.
1. Вероятность попадания в прямоугольный параллелепипед со сторонами, параллельными главным осям рассеивания
Пусть область  представляет собой прямоугольный параллелепипед, ограниченный абсциссами
представляет собой прямоугольный параллелепипед, ограниченный абсциссами 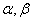 ординатами
ординатами 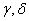 и аппликатами
и аппликатами 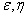 (рис. 9.6.1). Вероятность попадания в область
(рис. 9.6.1). Вероятность попадания в область  , очевидно, равна:
, очевидно, равна:
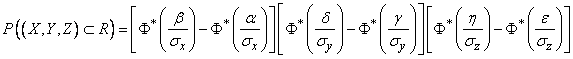 . (9.6.4)
. (9.6.4)

Рис. 9.6.1
2. Вероятность попадания в эллипсоид равной плотности
Рассмотрим эллипсоид равной плотности  , уравнение которого
, уравнение которого
 .
.
Полуоси этого эллипсоида пропорциональны главным средним квадратическим отклонениям:
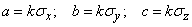 .
.
Пользуясь формулой (9.6.1) для 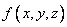 , выразим вероятность попадания в эллипсоид
, выразим вероятность попадания в эллипсоид  :
:
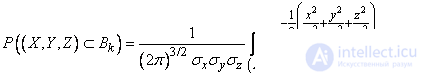 .
.
Перейдем от декартовых координат к полярным (сферическим) заменой переменных
 (9.6.5)
(9.6.5)
Якобиан преобразования (9.6.5) равен:
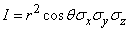 .
.
Переходя к новым переменным, имеем:
 .
.
Интегрируя по частям, получим:
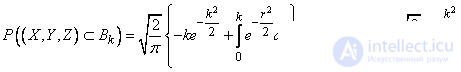 . (9.6.6)
. (9.6.6)
3. Об этом говорит сайт https://intellect.icu . Вероятность попадания в цилиндрическую область с образующей, параллельной одной из главных осей рассеивания
Рассмотрим цилиндрическую облает 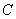 , образующая которой параллельна одной из главных осей рассеивания (например, оси
, образующая которой параллельна одной из главных осей рассеивания (например, оси 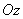 ), а направляющая есть контур произвольной области
), а направляющая есть контур произвольной области 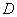 на плоскости
на плоскости 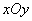 (рис. 9.6.2). Пусть область
(рис. 9.6.2). Пусть область 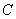 ограничена двумя плоскостями
ограничена двумя плоскостями  и
и 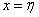 . Вычислим вероятность попадания в область
. Вычислим вероятность попадания в область 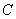 ; это есть вероятность произведения двух событий, первое из которых состоит в попадании точки
; это есть вероятность произведения двух событий, первое из которых состоит в попадании точки  в область
в область 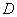 , а второе — в попадании величины
, а второе — в попадании величины 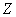 на участок
на участок  . Так как величины
. Так как величины  , подчинены нормальному закону в канонической форме, независимы, то независимы и эти два события. Поэтому
, подчинены нормальному закону в канонической форме, независимы, то независимы и эти два события. Поэтому
 (9.6.7)
(9.6.7)

Рис. 9.6.2.
Вероятность 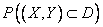 в формуле (9.6.7) может быть вычислена любым из способов вычисления вероятности попадания в плоскую область.
в формуле (9.6.7) может быть вычислена любым из способов вычисления вероятности попадания в плоскую область.
На формуле (9.6.7) основан следующий способ вычисления вероятности попадания в пространственную область 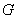 произвольной формы: область
произвольной формы: область  приближенно разбивается на ряд цилиндрических областей
приближенно разбивается на ряд цилиндрических областей  (рис. 9.6.3), и вероятность попадания в каждую из них вычисляется по формуле (9.6.7). Для применения этого способа достаточно начертить ряд фигур, представляющих собой сечения области
(рис. 9.6.3), и вероятность попадания в каждую из них вычисляется по формуле (9.6.7). Для применения этого способа достаточно начертить ряд фигур, представляющих собой сечения области  плоскостями, параллельными одной из координатных плоскостей. Вероятность попадания в каждую из них вычисляется по сетке рассеивания.
плоскостями, параллельными одной из координатных плоскостей. Вероятность попадания в каждую из них вычисляется по сетке рассеивания.
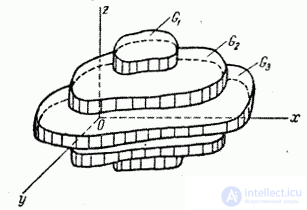
Рис. 9.6.3.
В заключение данной главы напишем общее для нормального закона в пространстве любого числа измерения 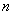 . Плотность распределения такого закона имеет вид:
. Плотность распределения такого закона имеет вид:
 , (9.6.8)
, (9.6.8)
где  — определитель матрицы
— определитель матрицы 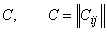 — матрица, обратная корреляционной матрице
— матрица, обратная корреляционной матрице  , т.е. если корреляционная матрица
, т.е. если корреляционная матрица
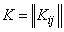 ,
,
то
 ,
,
где  - определитель корреляционной матрицы, а
- определитель корреляционной матрицы, а  - минор этого определителя, получаемый из него вычеркиванием
- минор этого определителя, получаемый из него вычеркиванием 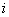 -й строки и
-й строки и 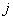 -го столбца. Заметим, что
-го столбца. Заметим, что
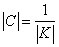 .
.
Из общего выражения (9.6.8) вытекают все формы нормального закона для любого числа измерений и для любых видов зависимости между случайными величинами. В частности, при 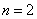 (рассеивание на плоскости) корреляционная матрица есть
(рассеивание на плоскости) корреляционная матрица есть
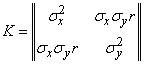 .
.
где 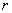 - коэффициент корреляции. Отсюда
- коэффициент корреляции. Отсюда
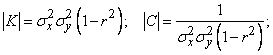
 .
.
Подставляя определитель матрицы  и ее члены в (9.6.8), получим формулу (9.1.1) для нормального закона на плоскости, с которой мы начали
и ее члены в (9.6.8), получим формулу (9.1.1) для нормального закона на плоскости, с которой мы начали 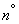 9.1.
9.1.
Информация, изложенная в данной статье про нормальный закон в пространстве трех измерений , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое нормальный закон в пространстве трех измерений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про нормальный закон в пространстве трех измерений
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ