13.3. Закон больших чисел (теорема Чебышева) кратко

Привет, Вы узнаете о том , что такое закон больших чисел теорема чебышева , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон больших чисел теорема чебышева , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В данном  мы докажем одну из простейших, но вместе с тем наиболее важных форм закона больших чисел - теорему Чебышева. Эта теорема устанавливает связь между средним арифметическим наблюденных значений случайной величины и ее математическим ожиданием.

 

Предварительно решим следующую вспомогательную задачу.

Имеется случайная величина 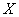 с математическим ожиданием  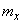и дисперсией 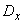. Над этой величиной производится  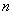независимых опытов и вычисляется среднее арифметическое всех наблюденных значений величины 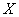. Требуется найти числовые характеристики этого среднего арифметического - математическое ожидание и дисперсию - и выяснить, как они изменяются с увеличением .

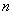Обозначим:

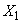 - значение величины  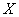в первом опыте;

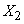 - значение величины  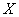во втором опыте, и т. д.

Очевидно, совокупность величин 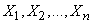 представляет собой  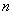независимых случайных величин, каждая из которых распределена по тому же закону, что и сама величина 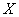. Рассмотрим среднее арифметическое этих величин:

.

Случайная величина  есть линейная функция независимых случайных величин 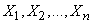. Об этом говорит сайт https://intellect.icu . Найдем математическое ожидание и дисперсию этой величины. Согласно правилам  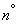10 для определении числовых характеристик линейных функций получим:

;

.

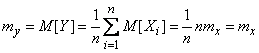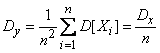Итак, математическое ожидание величины  не зависит от числа опытов 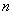 и равно математическому ожиданию наблюдаемой величины 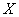; что касается дисперсии величины , то она неограниченно убывает с увеличением числа опытов и при достаточно большом 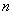 может быть сделана сколь угодно малой. Мы убеждаемся, что среднее арифметическое есть случайная величина со сколь угодно малой дисперсией и при большом числе опытов ведет себя почти как не случайная.

Теорема Чебышева и устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Она формулируется следующим образом:

При достаточно большом числе независимых опытов среднее арифметическое наблюденных значении случайной величины сходится по вероятности к ее математическому ожиданию.

Запишем теорему Чебышева в виде формулы. Для этого напомним смысл термина «сходится по вероятности». Говорят, что случайная величина  сходится по вероятности к величине 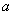, если при увеличении  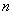вероятность того, что  и 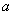 будут сколь угодно близки, неограниченно приближается к единице, а это значит, что при достаточно большом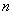 

,

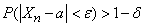где  - произвольно малые положительные числа.

Запишем в аналогичной форме теорему Чебышева. Она утверждает, что при увеличении 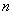 среднее арифметическое  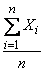сходится по вероятности к 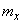, т. е.

.             (13.3.1)

Докажем это неравенство.

Доказательство. Выше было показано, что величина

имеет числовые характеристики

; .

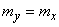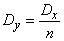Применим к случайной величине  неравенство Чебышева, полагая :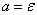

.

Как бы мало ни было число 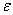, можно взять  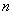таким большим, чтобы выполнялось неравенство

где 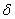 - сколь угодно малое число.

Тогда

,

откуда, переходя к противоположному событию, имеем:

,

что и требовалось доказать.

 

Информация, изложенная в данной статье про закон больших чисел теорема чебышева , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон больших чисел теорема чебышева и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про закон больших чисел теорема чебышева