Случайные величины, способы задания, примеры

Сразу хочу сказать, что здесь никакой воды про случайные величины, и только нужная информация. Для того чтобы лучше понимать что такое случайные величины, случайная величина , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.

случайная величина (случайная переменная, случайное значение) — это математическое понятие, служащее для представления случайных явлений, когда для них может быть определена их вероятность, то есть мера возможности наступления.

не путать с случайным событием.

Случайная величина является одним из основных понятий теории вероятностей. Для обозначения случайной величины в математике принято использовать греческую букву «кси» .

Случайная величина определяется следующим образом. Пусть — вероятностное пространство, — измеримое пространство. Тогда случайной величиной на пространстве элементарных событий со значениями в фазовом пространстве называется измеримая функция .

Примером объектов, для представления состояния которых требуется применение случайных величин являются микроскопические объекты, описываемые квантовой механикой. Случайными величинами описываются события передачи наследственных признаков от родительских организмов к их потомкам (см. Законы Менделя). К случайным относятся события радиоактивного распада ядер атомов.

Существует ряд задач математического анализа и теории чисел для которых участвующие в их формулировках функции целесообразно рассматривать как случайные величины , определенные на подходящих вероятностных пространствах

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Примеры случайных величин:

• 1) число попаданий при трех выстрелах;
• 2) число вызовов, поступавших на телефонную станцию за сутки;
• 3) частота попадания при 10 выстрелах.

Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.

Так, в примере 1) эти значения:

0, 1, 2, 3;

в примере 2):

1,2, 3, 4, …;

в примере 3)

0; 0,1; 0,2; …; 1,0.

Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.

Существуют случайные величины другого типа, например:

• 1) абсцисса точки попадания при выстреле;
• 2) ошибка взвешивания тела на аналитических весах;
• 3) скорость летательного аппарата в момент выхода на заданную высоту;
• 4) вес наугад взятого зерна пшеницы.

Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще – границы неопределенные, расплывчатые.

Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.

Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей оперировала по преимуществу с событиями, то современная теория вероятностей предпочитает, где только возможно, оперировать со случайными величинами.

Приведем примеры типичных для теории вероятностей приемов перехода от событий к случайным величинам.

Производится опыт, в результате которого может появиться или не появиться некоторое событие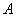. Вместо события 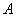можно рассмотреть случайную величину 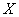, которая равна 1, если событие 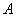происходит, и равна 0, если событие 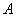не происходит. Случайная величина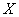, очевидно, является прерывной; она имеет два возможных значения: 0 и 1. Эта случайная величина называется характеристической случайной величиной события 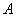. На практике часто вместо событий оказывается удобнее оперировать их характеристическими случайными величинами. Например, если производится ряд опытов, в каждом из которых возможно появление события 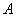, то общее число появлений события равно сумме характеристических случайных величин события 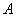во всех опытах. При решении многих практических задач пользование таким приемом оказывается очень удобным.

С другой стороны, очень часто для вычисления вероятности события оказывается удобно связать это событие с какой-то непрерывной случайной величиной (или системой непрерывных величин).

Рис. 2.4.1.

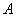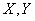Пусть, например, измеряются координаты какого-то объекта О для того, чтобы построить точку М, изображающую этот объект на панораме (развертке) местности. Нас интересует событие , состоящее в том, что ошибка R в положении точки М не превзойдет заданного значения (рис. 2.4.1). Обозначим случайные ошибки в измерении координат объекта. Очевидно, событие 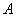равносильно попаданию случайной точки М с координатами 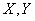в пределы круга радиуса с центром в точке О. 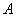Другими словами, для выполнения события случайные величины 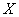и должны удовлетворять неравенству

. (2.4.1)

Вероятность события 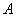есть не что иное, как вероятность выполнения неравенства (2.4.1). Эта вероятность может быть определена, если известны свойства случайных величин .

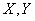Такая органическая связь между событиями и случайными величинами весьма характерна для современной теории вероятностей, которая, где только возможно, переходит от «схемы событий» к «схеме случайных величин». Последняя схема сравнительно с первой представляет собой гораздо более гибкий и универсальный аппарат для решения задач, относящихся к случайным явлениям.

История

Роль случайной величины, как одного из основных понятий теории вероятностей, впервые была четко осознана П. Л. Чебышевым, который обосновал общепринятую на сегодня точку зрения на это понятие (1867) . Понимание случайной величины как частного случая общего понятия функции, пришло значительно позднее, в первой трети 20 века. Впервые полное формализованное представление основ теории вероятностей на базе теории меры было разработано А. Н. Колмогоровым (1933) , после которого стало ясным, что случайная величина представляет собой измеримую функцию, определенную на вероятностном пространстве. В учебной литературе эта точка зрения впервые последовательно проведена У. Феллером (см. предисловие к , где изложение строится на основе понятия пространства элементарных событий и подчеркивается, что лишь в этом случае представление случайной величины становится содержательным).

Основные сведения

Функция распределения

Распределением вероятностей случайной величины называется функция на сигма-алгебре фазового пространства, определенная следующим образом:

, где (распределение вероятностей представляет собой вероятностную меру в фазовом пространстве ).

В случае, если фазовое пространство случайной величины представляет собой множество вещественных чисел , с борелевской σ-алгебры , то функция распределения равна вероятности того, что значение случайной величины меньше вещественного числа . Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна . Преимущество использования функции распределения заключается в том, что с ее помощью удается достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения. Например, если случайная величина принимает значения +1 и −1 с одинаковой вероятностью 1/2, то случайные величины и описываются одной и той же функцией распределения F(x).

Если случайная величина дискретная, то полное и однозначное математическое описание ее распределения определяется указанием функции вероятностей всех возможных значений этой случайной величины. Примерами дискретных случайных величин являются величины, имеющие биномиальный и пуассоновский законы распределения.

Эквивалентные случайные величины

Случайные функции и в фазовом пространстве называется эквивалентными, если для любого множества события и совпадают с вероятностью единица:

, где операция симметрической разности двух множеств.

Для сепарабельного фазового пространства эквивалентность означает, что величины и совпадают с вероятностью единица, т. е. .

Совместное распределение случайных величин. Независимые случайные величины

Совместным распределением вероятностей случайных величин на пространстве элементарных событий в соответствующих фазовых пространствах , называется функция , определенная на множествах как

.

Распределение вероятностей как функция на полукольце множеств вида в произведение пространств представляет собой функцию распределения. Случайные величины называются независимыми, если при любых

.

Для всякого семейства распределений в соответствующих фазовых пространствах ( параметр принадлежит произвольному множеству ) существует семейство случайных величин на некотором пространстве элементарных событий в соответствующих фазовых пространствах с распределением независимых между собой (т. е. любые случайные величины , , являются независимыми).

Типы случайных величин

Случайные величины классифицируются и называются в соответствии с типом их фазового пространства. Например:

• Случайной величина называется дискретной, если она принимает не более чем счетное количество значений. Дискретная случайная величины называется конечной, если она принимает конечное число значений. Случайная величина называется целочисленной, если она принимает в зависимости от случайного исхода одно из значений с соответствующими вероятностями .
• Измеримая функция называется многомерной случайной величиной или -мерным случайным вектором (относительно борелевской -алгебры на ). Эквивалентно этому является следующее определение: вектор , элементы которого являются случайные величины, называется многомерной случайной величиной или случайным вектором.
• Измеримая функция называется -мерным комплексным случайным вектором (также относительно соответствующей борелевской -алгебры).
• Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.
• Ограниченный выпуклый многогранник в -мерном линейном пространстве построенный в виде выпуклой оболочки более, чем из точек, являющихся реализацией случайного вектора в пространстве , называется случайным выпуклым многогранником.

Случайный процесс

Пусть — измеримое пространство, множество значений параметра . Об этом говорит сайт https://intellect.icu . Функция параметра , значениями которой являются случайные величины на пространстве элементарных событий в фазовом пространстве , называется случайным процессом в фазовом пространстве . Всевозможные совместные распределения вероятностей значений :

называются конечномерными распределениями вероятностей случайного процесса .

Числовые характеристики случайных величин

Математическим ожиданием или средним значением случайной величины в линейном нормированном пространстве X на пространстве элементарных событий называется интеграл

( в предположении, что функция является интегрируемой).

Дисперсией случайной величины называется величина, равная:

.

В статистике для дисперсии часто употребляется обозначение или . Величина , равная

называется среднеквадратическим отклонением, стандартным отклонением или стандартным разбросом.

Ковариацией случайных величин и называется следующая величина:

=

(предполагается, что математическое ожидание определено).

Если = 0, то случайные величины и называются не коррелированными.

Если , , то величина

называется коэффициентом корреляции случайных величин.

Моментом порядка k случайной величины называется математическое ожидание , абсолютным моментом порядка k называется величина ; центральным моментом порядка k — величина .

Функциональные характеристики случайных величин

Производящая функция

Пусть целочисленная случайная величина, принимающая в зависимости от случайного исхода одно из значений с соответствующими вероятностями . Функция переменной , , определяемая формулой

,

называется производящей функцией распределения случайной величины . Она является аналитической функцией от , , и приведенная формула дает ее разложение в степенной ряд. Распределение вероятностей однозначно определяется своей производящей функцией:

где — значение производной в точке z = 0.
Производящая функция при фиксированном совпадает с математическим ожиданием случайной величины :

.

Если случайная величина имеет математическое ожидание и дисперсию , то

,

.

Для производящей функции случайной величины, равной сумме независимых случайных величин — с производящими функциями справедлива следующее:

.

Характеристическая функция

Пусть векторная случайная величина в -мерном действительном пространстве , где борелевская -алгебра. Функция переменной , называется функцией распределения случайной величины ( или функцией совместного распределения величин ). Функция

, где ,

переменной на — мерном действительном пространстве называется характеристической функцией случайной величины (или величин ). Она непрерывна и положительно определена в том смысле, что

для любых и любых чисел при этом . Всякая функция , обладающая указанными свойствами, является характеристической функцией некоторой случайной величины .

И функция распределения и характеристическая функция однозначно определяют распределение вероятностей , , случайной величины .

Семиинварианты

Если , то в некоторой окрестности точки функция (ветвь логарифма, равная нулю в нуле) непрерывно дифференцируется до порядка . Значение

называется семиинвариантом порядка k.

Условные вероятности и условные математические ожидания

Пусть — пространство элементарных событий и — некоторая -алгебра, содержащаяся в . Условная вероятность события относительно -алгебры , обозначаемая , определяется как неотрицательная функция от элементарных исходов , , измеримая относительно , для которой

для любых . Функция на множестве элементарных событий определена однозначно для почти всех элементарных исходов и представляет собой плотность распределения , , относительно распределения на -алгебре .
Условная вероятность , рассматриваемая как функция со значениями в нормированном пространстве всех интегрированных (действительных и комплексных) функций на , представляет собой обобщенную меру на -алгебре пространства , вариация которой есть

.

Всякая случайная (действительная или комплексная ) величина , имеющая математическое ожидание (т.е. являющаяся интегрируемой функцией на пространстве с мерой ), интегрируема по отношению к обобщенной мере . Соответствующий интеграл

называется условным математическим ожиданием случайной величины .

Теорема Байеса

В терминах событий для случайной величины и событий и , при условии, что справедлива формула Байеса :

Для полного набора попарно несовместных событий и любого события с учетом формулы полной вероятности :

справедлива теорема Байеса:

.

В разных источниках, используется различная терминология для различных представлений теоремы Байеса.

Функции от случайных величин

Если — борелевская функция, а — случайная величина, то ее функциональное преобразование также является случайной величиной. Например, если — стандартная нормальная случайная величина, то случайная величина имеет распределение хи-квадрат с одной степенью свободы. Многие распределения, в том числе распределение Фишера, распределение Стьюдента являются распределениями функциональных преобразований нормальных случайных величин.

Если и с совместным распределением , а — некоторая борелевская функция, то для справедливо :

.

Если , и независимы, то . Применяя теорему Фубини получаем:

и аналогично

.

Если и функции распределения, то функцию

называют сверткой и и обозначают .
Характеристическая функция суммы независимых случайных величин и является фурье-преобразование свертки функций распределения и и равна произведения характеристических функций и :

.

Центральные предельные теоремы

Центральные предельные теоремы (ЦПТ)— класс теорем, утверждающих, что сумма большого количества независимых случайных величин с конечными дисперсиями, вклад в сумму каждой из которых невелик, имеет распределение, близкое к нормальному. Первоисточником исследований в области условий, при выполнений которых распределение суммы случайных величин с увеличением их количества сходится к нормальному стала локальная теорема Муавра — Лапласа.

Способы задания

Задать случайную величину, описав этим все ее вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных ее значений.

Примеры

Дискретная случайная величина (ДСВ)

Примерами дискретной случайной величины могут служить показания спидометра или измерения температуры в конкретные моменты времени.

Подбрасывание монеты

Все возможные исходы подбрасывания монеты могут быть описаны пространством элементарных событий орел, решка или кратко . Пусть случайная величина равна выигрышу в результате подбрасывания монеты. Пусть выигрыш будет 10 рублей каждый раз, когда монета выпадает орлом, и −33 рубля при выпадении решки. Математически эту функцию выигрыша можно представить так:

Если монета идеальная, то выигрыш будет иметь вероятность, заданную как:

где — вероятность получения рублей выигрыша при одном подбрасывании монеты.

Бросание игральных костей

Случайная величина также может быть использована для описания процесса бросания игральных костей, а также для расчета вероятности конкретного исхода таких бросков. В одном из классических примеров данного эксперимента используются две игральные кости и , каждая из которых может принимать значения из множества {1, 2, 3, 4, 5, 6} (количество очков на сторонах костей). Общее количество очков выпавших на костях и будет значением нашей случайной величины , которая задается функцией:

и (если кости идеальные) функция вероятности для задается через:

,

где — сумма очков на выпавших костях.

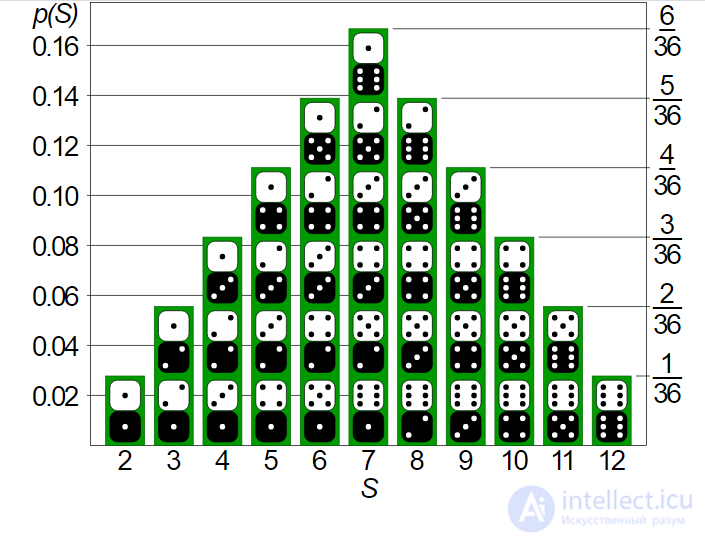
Если пространство исходов равно множеству всех возможных комбинаций очков на двух костях, и случайная величина равна сумме этих очков, тогда S — дискретная случайная величина, чье распределение описывается функцией вероятности, значение которой изображено как высота соответствующей колонки.

Колода карт

Пусть экспериментатор тянет наугад одну из карт в колоде игральных карт. Тогда будет представлять одну из вытянутых карт; здесь не число, а карта — физический объект, название которого обозначается через символ . Тогда функция , принимая в качестве аргумента «название» объекта, вернет число, с которым мы будем в дальнейшем ассоциировать карту . Пусть в нашем случае экспериментатор вытянул Короля Треф, то есть , тогда после подставления этого исхода в функцию , мы получим уже число, например, 13. Это число не является вероятностью вытягивания короля из колоды или любой другой карты. Это число является результатом перевода объекта из физического мира в объект математического мира, ведь с числом 13 уже можно проводить математические операции, в то время как с объектом эти операции проводить было нельзя.

Биноминальные случайные величины

Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта раз. В каждом опыте «успех» может наступить с вероятностью , «неудача» — с вероятностью . Закон распределения в этом случае определяется формулой Бернулли:

.

Пуассоновские случайные величины

Если при стремлении к бесконечности произведение остается равной константе , то биномиальный закон распределения сходится к закону Пуассона, который описывается следующей формулой:

,

где

• символ «» обозначает факториал,
• — основание натурального логарифма.

Непрерывная случайная величина

Другой класс случайных величин — такие, для которых существует неотрицательная функция , удовлетворяющая при любых равенству . Случайные величины, удовлетворяющие этому свойству называются непрерывными, а функция называется плотностью распределения вероятностей.

Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

Рост случайного прохожего

Пусть в одном из экспериментов нужно случайным образом выбрать одного человека (обозначим его как ) из группы испытуемых, пусть тогда случайная величина выражает рост выбранного нами человека. В этом случае, с математической точки зрения, случайная величина интерпретируется как функция , которая трансформирует каждого испытуемого в число — его рост . Для того чтобы рассчитать вероятность того, что рост человека попадет в промежуток между 180 см и 190 см, или вероятность того, что его рост будет выше 150 см, нужно знать распределение вероятности , которое в совокупности с и позволяет рассчитывать вероятности тех или иных исходов случайных экспериментов.

Вау!! 😲 Ты еще не читал? Это зря!

• Алгебра событий
• случайнные процессы
• ДСВ Дискретная случайная велична дискретные случайные величины , дсв ,
• НСВ Непрерывная случайная велична непрерывные случайные величины , нсв , непрерывная случайные величина ,
• Закон больших чисел
• Случайное событие
• Теорема Байеса
• моделирование случаного события
• Случайные события
• Смешанная случайная величина

А как ты думаешь, при улучшении случайные величины, будет лучше нам? Надеюсь, что теперь ты понял что такое случайные величины, случайная величина и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ