13.8. Центральная предельная теорема для одинаково распределенных слагаемых кратко

Привет, Вы узнаете о том , что такое центральная предельная теорема для одинаково распределенных слагаемых, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое центральная предельная теорема для одинаково распределенных слагаемых , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых. Здесь мы сформулируем и докажем одну из самых простых форм центральной предельной теоремы, относящуюся к случаю одинаково распределенных слагаемых.

 

Теорема. Если 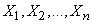 - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием  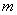и дисперсией 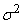, то при неограниченном увеличении  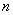закон распределения суммы

                            (13.8.1)

неограниченно приближается к нормальному.

Доказательство.

Проведем доказательство для случая непрерывных случайных величин 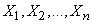 (для прерывных оно будет аналогичным).

Согласно второму свойству характеристических функций, доказанному в предыдущем 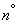, характеристическая функция величины  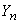представляет собой произведение характеристических функций слагаемых. Случайные величины  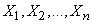имеют один и тот же закон распределения с плотностью  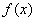и, следовательно, одну и ту же характеристическую функцию

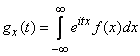.                       (13.8.2)

Следовательно, характеристическая функция случайной величины 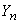 будет

.                              (13.8.3)

Исследуем более подробно функцию 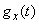. Представим ее в окрестности точки  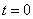по формуле Маклорена с тремя членами:

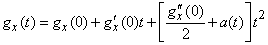,                          (13.8.4)

где 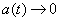 при .

Найдем величины 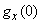, , 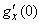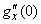. Полагая в формуле (13.8.2)  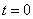имеем:

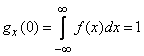.                                  (13.8.5)

Продифференцируем (13.8.2) по :

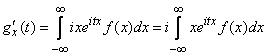.               (13.8.6)

Полагая в (13.8.6) 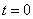, получим:

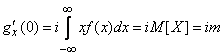.              (13.8.7)

Очевидно, не ограничивая общности, можно положить 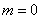 (для этого достаточно перенести начало отсчета в точку 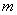). Об этом говорит сайт https://intellect.icu . Тогда

.

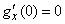Продифференцируем (13.8.6) еще раз:

,

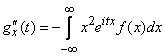отсюда

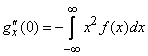.                     (13.8.8)

При 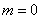 интеграл в выражении (13.8.8) есть не что иное, как дисперсия величины  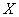с плотностью 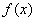, следовательно

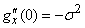.             (13.8.9)

Подставляя в (13.8.4) ,  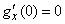и 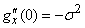, получим:

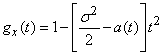.                 (13.8.10)

Обратимся к случайной величине 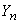. Мы хотим доказать, что ее закон распределения при увеличении  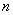приближается к нормальному. Для этого перейдем от величины  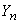к другой («нормированной») случайной величине

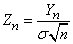.                (13.8.11)

Эта величина удобна тем, что ее дисперсия не зависит от 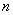 и равна единице при любом 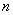. В этом нетрудно убедиться, рассматривая величину  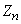как линейную функцию независимых случайных величин 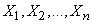, каждая из которых имеет дисперсию 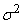. Если мы докажем, что закон распределения величины  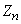приближается к нормальному, то, очевидно, это будет справедливо и для величины 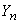, связанной с  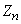линейной зависимостью (13.8.11).

Вместо того чтобы доказывать, что закон распределения величины 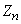 при увеличении  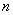приближается к нормальному, покажем, что ее характеристическая функция приближается к характеристической функции нормального закона.

Найдем характеристическую функцию величины 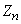. Из соотношения (13.8.11), согласно первому свойству характеристических функций (13.7.8), получим

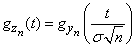,                        (13.8.12)

где 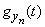 - характеристическая функция случайной величины .

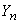Из формул (13.8.12) и (13.8.3) получим

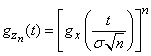                                 (13.8.13)

или, пользуясь формулой (13.8.10),

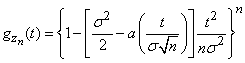.                    (13.8.14)

Прологарифмируем выражение (13.8.14):

.

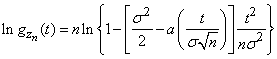Введем обозначение

.              (13.8.15)

Тогда

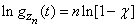.                                   (13.8.16)

Будем неограниченно увеличивать 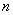. При этом величина 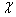, согласно формуле (13.8.15), стремится к нулю. При значительном  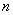ее можно считать весьма малой. Разложим,  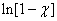в ряд и ограничимся одним членом разложения (остальные при  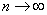станут пренебрежимо малыми):

.

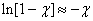Тогда получим

.

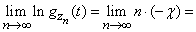
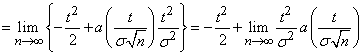По определению функция  стремится к нулю при ; следовательно,

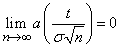
и

,

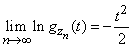откуда

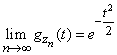.                 (13.8.17)

Это есть не что иное, как характеристическая функция нормального закона с параметрами 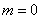,  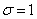(см. пример 2,  13.7).

Таким образом, доказано, что при увеличении 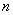 характеристическая функция случайной величины  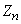неограниченно приближается к характеристической функции нормального закона; отсюда заключаем что и закон распределения величины  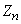(а значит и величины 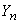) неограниченно приближается к нормальному закону. Теорема доказана.

Мы доказали центральную предельную теорему для частного, но важного случая одинаково распределенных слагаемых. Однако в достаточно широком классе условий она справедлива и для неодинаково распределенных слагаемых. Например, А. М. Ляпунов доказал центральную предельную теорему для следующих условий:

,                        (13.8.18)

где 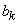 - третий абсолютный центральный момент величины :

       .

 - дисперсия величины .

Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремы является условие Линдеберга: при любом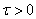 

,

где 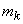 - математическое ожидание,  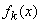- плотность распределения случайной величины , .

 

 

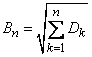Информация, изложенная в данной статье про центральная предельная теорема для одинаково распределенных слагаемых , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое центральная предельная теорема для одинаково распределенных слагаемых и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про центральная предельная теорема для одинаково распределенных слагаемых