12.3. Закон распределения немонотонной функции одного случайного аргумента кратко

Привет, Вы узнаете о том , что такое закон распределения немонотонной функции одного случайного аргумента, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон распределения немонотонной функции одного случайного аргумента , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Имеется непрерывная случайная величина 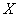 с плотностью распределения 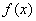; другая величина  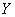связана с  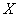функциональной зависимостью:

,

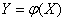причем функция 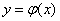 на участке  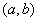возможных значений аргумента не монотонна (рис. 12.3.1).

 

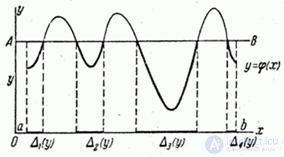
Рис. 12.3.1.

Найдем функцию распределения 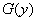 величины 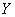. Для этого снова проведем прямую 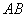, параллельную оси абсцисс, на расстоянии  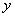от нее и выделим те участки кривой 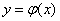, на которых выполняется условие 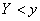. Пусть этим участкам соответствуют участки оси абсцисс: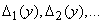 

Событие 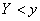 равносильно попаданию случайной величины  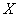на один из участков  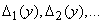- безразлично, на какой именно. Поэтому

.

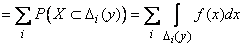Таким образом, для функции распределения величины 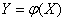 имеем формулу:

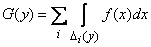.                                (12.3.1)

Границы интервалов 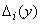 зависят от  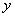и при заданном конкретном виде функции  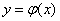могут быть выражены как явные функции 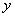. Об этом говорит сайт https://intellect.icu . Дифференцируя  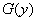по величине 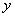, входящей в пределы интегралов, получим плотность распределения величины :

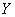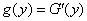.             (12.3.2)

Пример. Величина 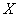 подчинена закону равномерной плотности на участке от  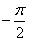до :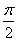

Найти закон распределения величины .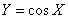

Решение. Строим график функции 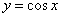 (рис. 12.3.2). Очевидно, 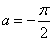,  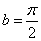и в интервале  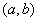функция  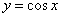немонотонна.

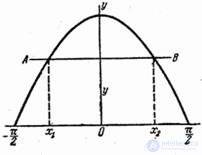
Рис. 12.3.2.

Применяя формулу (12.3.1), имеем:

.

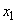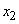Выразим пределы  и  через :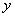

; .

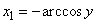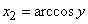Отсюда

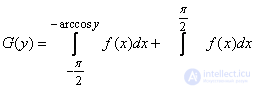.                  (12.3.3)

Чтобы найти плотность 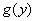, не будем вычислять интегралы в формуле (12.3.3), а непосредственно продифференцируем это выражение по переменной , входящей в пределы интегралов:

.

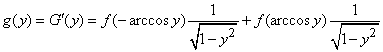Имея в виду, что 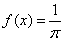, получим:

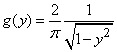.                 (12.3.4)

Указывая для 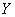 закон распределения (12.3.4), следует оговорить, что он действителен лишь в пределах от 0 до 1, т.е. в тех пределах, в которых меняется  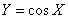при аргументе 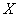, заключенном между  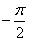и 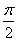. Вне этих пределов плотность  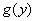равна нулю.

График функции 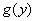 дан на рис. 12.3.3. При  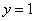кривая  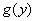имеет ветвь, уходящую на бесконечность.

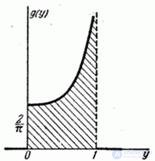
Рис. 12.3.3.

Информация, изложенная в данной статье про закон распределения немонотонной функции одного случайного аргумента , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон распределения немонотонной функции одного случайного аргумента и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про закон распределения немонотонной функции одного случайного аргумента