Лекция
Привет, сегодня поговорим про производящая функция канонического преобразования , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое производящая функция канонического преобразования , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
В гамильтоновой механике каноническое преобразование (также контактные преобразования) — это преобразование канонических переменных и гамильтониана не меняющие общий вид уравнений Гамильтона для любой гамильтоновой системы. Канонические преобразования могут быть введены и в квантовом случае как не меняющие вид уравнений Гейзенберга. Они позволяют свести задачу с определенным гамильтонианом к задаче с более простым гамильтонианом как в классическом, так и в квантовом случае. Канонические преобразования образуют группу.
Преобразования
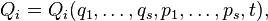

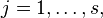 , где
, где  — число степеней свободы,
— число степеней свободы,
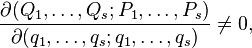
называются каноническими, если это преобразование переводит уравнения Гамильтона с функцией Гамильтона  :
:
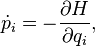

в уравнения Гамильтона с функцией Гамильтона  :
:
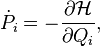
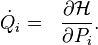
Переменные 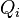 и
и  называются новыми координатами и импульсами, соответственно, а
называются новыми координатами и импульсами, соответственно, а  и
и  — старыми координатами и импульсами.
— старыми координатами и импульсами.
Из инвариантности интеграла Пуанкаре-Картана и теореме Ли Хуа-чжуна о его единственности можно получить:

где постоянную  называют валентностью канонического преобразования,
называют валентностью канонического преобразования,  — полный дифференциал некоторой функции
— полный дифференциал некоторой функции  (предполагается, что
(предполагается, что  и
и 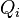 также выражены через старые переменные). Она называется производящей функцией канонического преобразования. Канонические преобразования взаимнооднозначно определяются производящей функцией и валентностью.
также выражены через старые переменные). Она называется производящей функцией канонического преобразования. Канонические преобразования взаимнооднозначно определяются производящей функцией и валентностью.
Канонические преобразования для которых  называется унивалентными. Так как при заданной производящей функции различные
называется унивалентными. Так как при заданной производящей функции различные  изменяют выражения для новых координат через старые, а также для гамильтониана только на константу, то часто рассматривают только унивалентные канонические преобразования.
изменяют выражения для новых координат через старые, а также для гамильтониана только на константу, то часто рассматривают только унивалентные канонические преобразования.
Производящая функция часто может быть выражена не через старые координаты и импульсы, а через любые две из четырех переменных  , причем выбор независим для каждого
, причем выбор независим для каждого  . Удобным оказывается выразить ее так, чтобы для каждого
. Удобным оказывается выразить ее так, чтобы для каждого 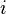 одна переменная был новой, а другая старой. Существует лемма утверждающая, что это можно сделать всегда. Дифференциал функции
одна переменная был новой, а другая старой. Существует лемма утверждающая, что это можно сделать всегда. Дифференциал функции 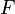 имеет явный вид полного дифференциала в том случае, когда она выражена через старые и новые координаты
имеет явный вид полного дифференциала в том случае, когда она выражена через старые и новые координаты  . При использовании других пар координат удобно перейти к функциям, дифференциал которых будет иметь явный вид полного дифференциала для соответствующих переменных. Для этого нужно сделать преобразования Лежандра исходной функции
. При использовании других пар координат удобно перейти к функциям, дифференциал которых будет иметь явный вид полного дифференциала для соответствующих переменных. Для этого нужно сделать преобразования Лежандра исходной функции 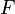 . Полученные функции называют производящими функциями канонического преобразования в соответствующих координатах. В случае когда выбор координат одинаков для всех
. Полученные функции называют производящими функциями канонического преобразования в соответствующих координатах. В случае когда выбор координат одинаков для всех 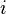 возможны четыре варианта выбора переменных, соответствующие функции принято обозначать номерами:
возможны четыре варианта выбора переменных, соответствующие функции принято обозначать номерами:

где для простоты введены векторы старых скоростей и импульсов  ,
, 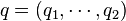 , аналогично и для новых скоростей и импульсов. Об этом говорит сайт https://intellect.icu . О таких производящих функциях говорят как о производящих функциях 1-го, 2-го, 3-го или 4-го типа соответственно.
, аналогично и для новых скоростей и импульсов. Об этом говорит сайт https://intellect.icu . О таких производящих функциях говорят как о производящих функциях 1-го, 2-го, 3-го или 4-го типа соответственно.
Пусть  — произвольная невырожденная функция старых координат, новых координат и времени:
— произвольная невырожденная функция старых координат, новых координат и времени:

кроме того, задано некоторое число  , тогда пара
, тогда пара  задает каноническое преобразование по правилу
задает каноническое преобразование по правилу
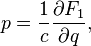


Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если неравен нулю якобиан:

Канонические преобразования, дополненные этим условием называют свободными.
Пусть  — произвольная невырожденная функция старых координат, новых координат и времени:
— произвольная невырожденная функция старых координат, новых координат и времени:

кроме того, задано некоторое число  , тогда пара
, тогда пара 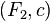 задает каноническое преобразование по правилу
задает каноническое преобразование по правилу
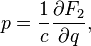
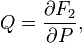

Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если неравен нулю якобиан:

Пусть  — произвольная невырожденная функция старых координат, новых координат и времени:
— произвольная невырожденная функция старых координат, новых координат и времени:

кроме того, задано некоторое число  , тогда пара
, тогда пара  задает каноническое преобразование по правилу
задает каноническое преобразование по правилу
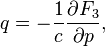


Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если не равен нулю якобиан:

Пусть  — произвольная невырожденная функция старых координат, новых координат и времени:
— произвольная невырожденная функция старых координат, новых координат и времени:

кроме того, задано некоторое число  , тогда пара
, тогда пара 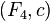 задает каноническое преобразование по правилу
задает каноническое преобразование по правилу


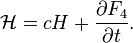
Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если неравен нулю якобиан:
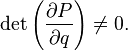
1. Тождественное преобразование
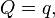
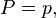
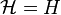
может быть получено при:

2. Если задать

то полученное преобразование будет иметь вид:


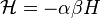
Таким образом, разделение канонических переменных на координаты и импульсы с математической точки зрения является условным.
3. Преобразование инверсии


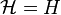
может быть получено при:

4. Точечные преобразования (преобразования при которых новые координаты выражаются только через старые координаты и время, но не старые импульсы.)
Они всегда могут быть заданы с помощью:

тогда

В частности, если

где  — ортогональная матрица:
— ортогональная матрица:

то
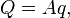
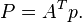
К точечным преобразования приводит и функция:
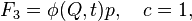
тогда
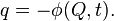
В частности функция

задает переход от декартовых координат к цилиндрическим.
5. Линейные преобразования переменных  системы с одной степенью свободы:
системы с одной степенью свободы:
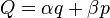

является унивалентным каноническим преобразованием при
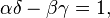
производящая функция:

Такие преобразования образуют специальную линейную группу 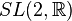 .
.
Действие, выраженное как функция координат и импульсов конечной точки

задает каноническое преобразование гамильтоновой системы.
Необходимое и достаточное условие каноничности преобразований может быть записано с помощью скобок Пуассона:


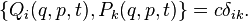
Кроме того, необходимым и достаточным условием каноничности преобразования является выполнение для произвольных функций 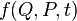 и
и 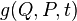 условия:
условия:
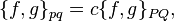
где под  и
и 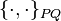 понимаются скобки Пуассона по старым и новым координатам соответственно.
понимаются скобки Пуассона по старым и новым координатам соответственно.
В случае унивалентных канонических преобразований:

и говорят, что скобки Пуассона инвариантны относительно таких преобразований. Иногда канонические преобразования так определяют (при этом каноническими преобразованиями считают только унивалентные).
Аналогично, необходимое и достаточное условие каноничности преобразований может быть записано с помощью скобок Лагранжа:
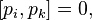

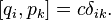
Надеюсь, эта статья про производящая функция канонического преобразования , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое производящая функция канонического преобразования и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про производящая функция канонического преобразования
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ