15.1. Теория случайных функций. Понятие о случайной функции кратко

Привет, Вы узнаете о том , что такое теория случайных функций понятие о случайной функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теория случайных функций понятие о случайной функции , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

До сих пор в нашем курсе теории вероятностей основным предметом исследования были случайные величины. Случайная величина характерна тем, что она в результате опыта принимает некоторое одно, заранее неизвестное, но единственное значение. Примерами таких случайных величин могут служить: абсцисса точки попадания при выстреле; ошибка радиодальномера при одном, единичном измерении дальности; горизонтальная ошибка наводки при одном выстреле и т. д.

 

Ограничиваясь рассмотрением подобных отдельных случайных величин, мы изучали случайные явления как бы «в статике», в каких-то фиксированных постоянных условиях отдельного опыта.

Однако такой элементарный подход к изучению случайных явлений в ряде практических задач является явно недостаточным. На практике часто приходится иметь дело со случайными величинами, непрерывно изменяющимися в процессе опыта. Примерами таких случайных величин могут служить: ошибка радиодальномера при непрерывном измерении меняющейся дальности; угол упреждения при непрерывном прицеливании по движущейся цели; отклонение траектории управляемого снаряда от теоретической в процессе управления или самонаведения.

Такие случайные величины, изменяющиеся в процессе опыта, мы будем в отличие от обычных случайных величин называть случайными функциями.

Изучением подобных случайных явлений, в которых случайность проявляется в форме процесса, занимается специальная отрасль теории вероятностей - теория случайных функций (иначе - теория случайных или стохастических процессов). Эту науку можно образно назвать «динамикой случайных явлений».

Теория случайных функций - новейший раздел теории вероятностей, развившийся, в основном, за последние два-три десятилетия. В настоящее время эта теория продолжает развиваться и совершенствоваться весьма быстрыми темпами. Это связано с непосредственными требованиями практики, в частности с необходимостью решения ряда технических задач. Известно, что за последнее время в технике все большее распространение получают системы с автоматизированным управлением. Соответственно все большие требования предъявляются к теоретической базе этого вида техники - к теории автоматического управления. Развитие этой теории невозможно без анализа ошибок, неизбежно сопровождающих процессы управления, которые всегда протекают в условиях непрерывно воздействующих случайных возмущений (так называемых «помех»). Эти возмущения по своей природе являются случайными функциями. Для того чтобы рационально выбрать конструктивные параметры системы управления, необходимо изучить ее реакцию на непрерывно воздействующие случайные возмущения, а единственным аппаратом, пригодным для такого исследования, является аппарат теории случайных функций.

В данной главе мы познакомимся с основными понятиями этой теории и с общей постановкой ряда практических задач, требующих применения теории случайных функций. Кроме того, здесь будут изложены общие правила оперирования с характеристиками случайных функций, аналогичные правилам оперирования с числовыми характеристиками обычных случайных величин.

Первым из основных понятий, с которыми нам придется иметь дело, является само понятие случайной функции. Это понятие настолько же шире и богаче понятия случайной величины, насколько математические понятия переменной величины и функции шире и богаче понятия постоянной величины.

Вспомним определение случайной величины. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее - какое именно. Дадим аналогичное определение случайной функции.

Случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, неизвестно заранее - какой именно.

Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией случайной функции. Если над случайней функцией произвести группу опытов, то мы получим группу или «семейство» реализаций этой функции.

Приведем несколько примеров случайных функций.

Пример 1. Об этом говорит сайт https://intellect.icu . Самолет-бомбардировщик на боевом курсе имеет теоретически постоянную воздушную скорость 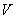. Фактически его скорость колеблется около этого среднего номинального значения и представляет собой случайную функцию времени. Полет на боевом курсе можно рассматривать как опыт, в котором случайная функция  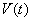принимает определенную реализацию (рис. 15.1.1).

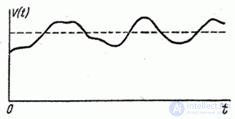
Рис. 15.1.1.

От опыта к опыту вид реализации меняется. Если на самолете установлен самопишущий прибор, то он в каждом полете запишет новую, отличную от других реализацию случайной функции. В результате нескольких полетов можно получить семейство реализаций случайной функции 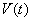 (рис. 15.1.2).

Рис. 15.1.2.

Пример 2. При наведении управляемого снаряда на цель ошибка наведения 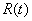 представляет собой отклонение центра массы снаряда от теоретической траектории, т. е. случайную функцию времени (рис. 15.1.3).

Рис. 15.1.3.

В том же опыте случайными функциями времени являются, например, перегрузка снаряда 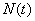, угол атаки  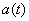и т. д.

Пример 3. При стрельбе с самолета по самолету перекрестие прицела в течение некоторого времени должно непрерывно совмещаться с целью - следить за ней. Операция слежения за целью сопровождается ошибками - так называемыми ошибками наводки (рис. 15.1.4).

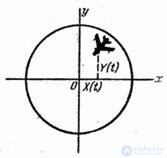
Рис. 15.1.4.

Горизонтальная и вертикальная ошибки наводки в процессе прицеливания непрерывно меняются и представляют собой две случайные функци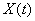и  и 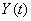. Реализации этих случайных функций можно получить в результате дешифровки снимков фотопулемета, фотографирующего цель в течение всего процесса слежения.

Число примеров случайных функций, встречающихся в технике, можно было бы неограниченно увеличивать. Действительно, в любом случае, когда мы имеем дело с непрерывно работающей системой (системой измерения, управления, наведения, регулирования), при анализе точности работы этой системы нам приходится учитывать наличие случайных воздействий (помех). Как сами помехи, так и вызванная ими реакция системы представляют собой случайные функции времени.

До сих пор мы говорили только о случайных функциях, аргументом которых является время . В ряде задач практики встречаются случайные функции, зависящие не от времени, а от других аргументов. Например, характеристики прочности неоднородного стержня могут рассматриваться как случайные функции абсциссы сечения 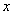. Температура воздуха в различных слоях атмосферы может рассматриваться как случайная функция высоты .

На практике встречаются также случайные функции, зависящие не от одного аргумента, а от нескольких. Например, аэрологические данные, характеризующие состояние атмосферы (температура, давление, ветер), представляют собой в общем случае случайные функции четырех аргументов: трех координат 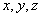 и времени .

В данном курсе мы будем рассматривать только случайные функции одного аргумента. Так как этим аргументом чаще всего является время, будем обозначать его буквой . Кроме того, условимся, как правило, обозначать случайные функции большими буквами 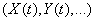 в отличие от неслучайных функций .

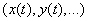Рассмотрим некоторую случайную функцию 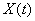. Предположим, что над ней произведено  независимых опытов, в результате которых получено  реализаций (рис. 15.1.5).

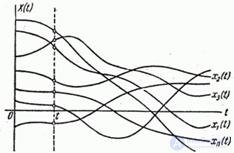
Рис. 15.1.5.

Обозначим их соответственно номеру опыта .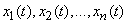

Каждая реализация, очевидно, есть обычная (неслучайная) функция. Таким образом, в результате каждого опыта случайная функция 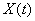 превращается в обычную, неслучайную функцию.

Зафиксируем теперь некоторое значение аргумента  и посмотрим, во что превратится при этом случайная функция 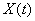. Очевидно, она превратится в случайную величину в обычном смысле слова. Условимся называть эту случайную величину сечением случайной функции, соответствующим данному . Если провести «сечение» семейства реализаций при данном  (рис. 15.1.5), мы получим  значений, принятых случайной величиной 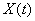 в  опытах.

Мы видим, что случайная функция совмещает в себе черты случайной величины и функции. Если зафиксировать значение аргумента, она превращается в обычную случайную величину; в результате каждого опыта она превращается в обычную (неслучайную) функцию.

В ходе дальнейшего изложения мы часто будем попеременно рассматривать одну и ту же функцию 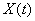 то как случайную функцию, то как случайную величину, в зависимости от того, рассматривается ли она на всем диапазоне изменения  или при его фиксированном значении.

 

Информация, изложенная в данной статье про теория случайных функций понятие о случайной функции , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое теория случайных функций понятие о случайной функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про теория случайных функций понятие о случайной функции