Теорема сложения вероятностей несовместных событий

Привет, сегодня поговорим про теорема сложения вероятностей несовместных событий, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое теорема сложения вероятностей несовместных событий , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

теорема сложения вероятностей несовместных событий

Теорема. Вероятность суммы конечного числа несовместных событий 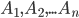 равна сумме вероятностей этих событий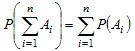(2.1)

Доказательство. Докажем эту теорему для случая суммы двух несовместных событи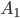й  и 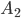.Пусть событию  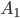благоприятствуют  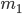элементарных исходов, а событию A2 :  m2  исходов. Так как события  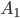и 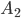 по условию теоремы несовместны, то событию A1+A2 благоприятствуют m1+m2 элементарных исходов из общего числа n исходов. Следовательно,,

где  — вероятность события ;  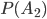— вероятность события .

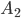Пример. Для отправки груза со склада может быть выделена одна из двух машин различного вида. Известны вероятности выделения каждой машины: .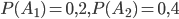

Тогда вероятность поступления к складу хотя бы одной из этих машин будет

P(А₁+А₂) = 0,2 + 0,4 = 0,6.

Условная вероятность

Во многих случаях вероятности появления одних событий зависят от того, произошло или нет другое событие. Например, вероятность своевременного выпуска машины зависит от поставки комплектующих изделий. Если эти изделия уже поставлены, то искомая вероятность будет одна. 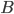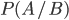Если же она определяется до поставки комплектующих, то ее значение, очевидно, будет другим.Вероятность события , вычисленная при условии, что имело место другое событие , называется условной вероятностью события и обозначается .В тех случаях, когда вероятность события  рассматривается при условии, что произошло два других события 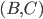, используется условная вероятность относительно произведения событий .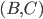

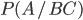Теорема умножения вероятностей

Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место

P(AB) = P(A)×P(B/A) = P(B)×P(A/B). Об этом говорит сайт https://intellect.icu . (2.2)

Доказательство. Предположим, что из 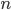 всевозможных элементарных исходов событию  благоприятствуют 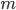 исходов, из которых  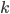исходов благоприятствуют событию 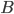. Тогда вероятность события  будет 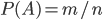, условная вероятность события  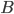относительно события будет .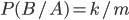

Произведению событий  и 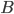 благоприятствуют только те исходы, которые благоприятствуют и событию  и событию 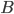одновременно, т.е.  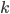исходов. Поэтому вероятность произведения событий  и 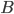равна.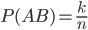

Умножим числитель и знаменатель этой дроби на .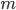

Получим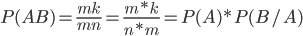.Аналогично доказывается и формула.

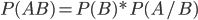Пример. На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие это холодильники. Найти вероятность того, что два взятых наугад холодильника будут с дефектами.

Решение. Вероятность того, что первый выбранный холодильник будет с дефектом, находится как отношение числа благоприятствующих исходов к общему числу возможных исходовP(A) = 5/35 = 1/7.Но после того, как был взят первый холодильник с дефектом, условная вероятность того, что и второй будет с дефектом, определяется на основе соотношения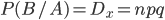

Искомая вероятность будет.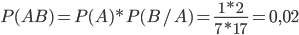

Если при наступлении события  вероятность события 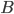 не меняется, то события  и 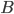 называются независимыми.В случае независимых событий вероятность их произведения равна произведению вероятностей этих событий

P(AB) = P(A)×P(B). (2.3)

Теорема умножения вероятностей легко обобщается на любое конечное число событий.

Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий, т.е.P(ABC....LM) = P(A)×P(B/A)×P(C/AB) P(M/AB...L). (2.4)

Для доказательства этой теоремы можно использовать метод математической индукции.

Теорема сложения вероятностей совместных событий

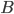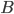Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.Пример. Поступление в магазин одного вида товара — событие . Поступление второго вида товара — событие . Поступить эти товары могут и одновременно. Поэтому  и - совместные события.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появленияP(A+B) = P(A) + P(B) — P(AB). (2.5)

Доказательство. Событие A+B наступит, если наступит одно из трех несовместных событий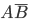,,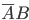 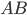. По теореме сложения вероятностей несовместных событий имеем(2.6)

Событие  произойдет, если наступит одно из двух несовместных событий: , .

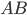Вновь применяя теорему сложения вероятностей несовместных событий, получаем .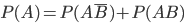

Откуда

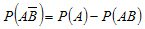(2.7)

Аналогично для события

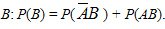
Откуда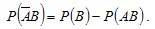.(2.8)

Подставив (2.7) и (2.8) в (2.6), находим

P(A+B) = P(A) + P(B) — P(AB).

Пример. Если вероятность поступления в магазин одного вида товара равна P(A) = 0,4,

а второго товара — P(B) = 0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна

P(A+B) = 0,4 + 0,5 — 0,4×0,5 = 0,7.

Надеюсь, эта статья про теорема сложения вероятностей несовместных событий, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое теорема сложения вероятностей несовместных событий и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ