Производящая функция моментов, определение и объяснение кратко

Привет, сегодня поговорим про производящая функция моментов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое производящая функция моментов, пфм , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

производящая функция моментов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.

Определение

Пусть есть случайная величина с распределением . Тогда ее производящей функцией моментов называется функция, имеющая вид:

.

Пользуясь формулами для вычисления математического ожидания, определение производящей функции моментов можно переписать в виде:

,

то есть производящая функция моментов — это двустороннее преобразование Лапласа распределения случайной величины (с точностью до отражения).

Дискретные и абсолютно непрерывные случайные величины

Если случайная величина дискретна, то есть , то

.

Пример. Пусть имеет распределение Бернулли. Тогда

.

Если случайная величина абсолютно непрерывна, то есть она имеет плотность , то

.

Пример. Пусть имеет стандартное непрерывное равномерное распределение. Тогда

.

Свойства производящих функций моментов

Свойства производящих функций моментов во многом аналогичны свойствам характеристических функций в силу похожести их определений.

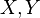• Производящая функция моментов однозначно определяет распределение. Пусть суть две случайные величины, и 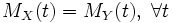. Тогда 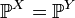. В частности, если обе величины абсолютно непрерывны, то совпадение производящих функций моментов влечет совпадение плотностей. Если обе случайные величины дискретны, то совпадение производящих функций моментов влечет совпадение функций вероятности.
• Производящая функция моментов как функция случайной величины однородна:

.

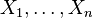• Производящая функция моментов суммы независимых случайных величин равна произведению их производящих функций моментов. Об этом говорит сайт https://intellect.icu . Пусть суть независимые случайные величины. Обозначим 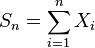. Тогда

.

Вычисление моментов

.

Объясняем производящую функцию моментов

1. Начнем с главного — что такое “момент” в вероятности и статистике?

Скажем, нас интересует случайная переменная X.

Моменты — это ожидаемые значения X, например, E(X), E(X²), E(X³) и т.д.

Первый момент — E(X),

Второй момент — E(X²),

Третий момент — E(X³),

…

n-й момент — E(X^n).

Нам очень хорошо знакомы первые два момента: математическое ожидание μ = E(X) и дисперсия E(X²) − μ². Это важные характеристики X. Математическое ожидание — это среднее значение случайной величины, дисперсия — мера разброса значений. Но должны быть и другие функции, также определяющие распределение. Например, третий момент указывает на асимметрию, четвертый — насколько тяжелы хвосты распределения.

Моменты говорят нам о свойствах распределения.

2. Что же такое производящая функция моментов?

Эта функция определяет распределение значений случайной величины— E(X), E(X²), E(X³), … , E(X^n).

Определение производящей функции моментов

Глядя на определение, вы можете сказать:

“Меня не интересует E(e^tx). Мне нужно E(X^n).”

Возьмите производную от пфм n раз и подставьте t = 0. Так вы получите E(X^n).

Как получить моменты из ПФМ

3. Почему n-й момент является n-й производной ПФМ?

Для доказательства используем ряды Тейлора:

Затем берем ожидаемое значение:

Теперь берем производную по t:

Если возьмем другую производную (то есть производную дважды), получим E(X²).
Снова возьмем производную (третью), получим E(X³), и так далее.

Когда я впервые увидела ПФМ, я не поняла роль t в функции, потому что t показалась произвольной переменной, которая не особенно меня интересовала. Между тем t является вспомогательной переменной — мы вводим t, чтобы использовать исчисление (производные) и обнулить значения (которые нас не интересуют).

Подождите… но мы можем вычислить моменты, используя определение ожидаемых значений. Зачем нам ПФМ?

Определение ожидаемых значений (если вы хотите разобраться в разнице между X и x, почитайте ниже)

В чем отличие ? от ??

Это математические соглашения. ? — стохастическое, а ? —  детерминированное. Допустим, ? —число, которое мы получили, бросив кубик. То есть ? может быть любым числом из множества {1,2,3,4,5,6}. Но как только кубик брошен, значение ? определено. ? = ? означает, что случайная величина ? принимает конкретное значение ?. Итак:

• ? — случайная величина, обозначаемая заглавной буквой.
• ? — определенное (фиксированное) значение, которое может принимать случайная величина. Например, ?1, ?2, …, ?n может быть выборкой, соответствующей случайной величине X.

Следовательно, совокупная вероятность P(? ≤ ?) означает, что диапазон функции ? меньше определенного значения ?

4. Так зачем нам нужна ПФМ?

Для удобства. Производящая функция моментов упрощает вычисление моментов.

Как?

В учебнике математики написано: “найдите производящую функцию момента биномиального (n, p), пуассонового (λ), экспоненциального (λ), нормального (0, 1) распределений и так далее”. Однако в нем никогда не объяснялось, почему ПФМ полезна и удобна.

Я думаю, пример ниже порадует вас — самый яркий пример, где есть простое использование ПФМ: ПФМ экспоненциального распределения. (Не знакомы с экспоненциальным распределением? ? Экспоненциальное распределение: восприятие, происхождение, применение)

Начнем с плотности вероятности:

Плотность вероятности экспоненциального распределения

Продифференцируем экспоненциальную ПФМ:

Чтобы ПФМ существовала, должно существовать ожидаемое значение E(e^tx).
Вот почему t — λ < 0 — важное условие: в противном случае интеграл не будет сходиться (это называется тестом на сходимость и проверяется первым делом, когда нужно определить, сходится интеграл или расходится).

Раз у нас есть ПФМ: λ/(λ-t), вычисление моментов становится просто вопросом взятия производных, что проще, чем использование интегралов для расчета ожидаемого значения напрямую.

Используя ПФМ, можно находить моменты при помощи производных, а не интегралов!

Несколько замечаний:

1. Для любой действительной ПФМ M(0) = 1.
   Всякий раз при вычислении ПФМ подставляйте t = 0 и смотрите, получите ли 1.
2. Моменты помогают подробнее описать распределение. Например, можно полностью описать нормальное распределение по первым двум моментам — математическому ожиданию и дисперсии. Чем больше моментов вы знаете, тем больше вы знаете о распределении. Если вы никогда не встречали человека, но знаете его рост, вес, цвет кожи, хобби и т.д., вы по-прежнему не знаете его полностью, но у вас есть много информации о нем.
3. Прелесть ПФМ в том, что, получив ПФМ (когда ожидаемое значение существует), вы можете получить любой n-й момент, так как ПФМ кодирует все моменты случайной переменной в одну функцию, из которой их легко снова извлечь.
4. Распределение вероятностей однозначно определяется его ПФМ. Если у двух случайных переменных одинаковая ПФМ, они должны иметь одинаковое распределение.
5. Одно из важнейших свойств распределения — насколько тяжелы его хвосты, особенно, в управлении финансовыми рисками. Если вспомнить финансовый кризис 2008 года, в основе которого по сути лежали неудачные определения вероятностей редких событий, управляющие рисками недооценили эксцесс (“выпуклость”) финансового обеспечения, лежащего в основе торговых позиций фонда. Иногда выглядящие случайными распределения с гипотетически гладкими кривыми риска могут содержать скрытые эксцессы. И мы можем найти их, используя ПФМ!

Cм. также

• понятие - производящая функция ,
• производящая функция последовательности , генератриса ,
• производящая функция канонического преобразования ,

Надеюсь, эта статья про производящая функция моментов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое производящая функция моментов, пфм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про производящая функция моментов