9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания кратко

Привет, Вы узнаете о том , что такое вероятность попадания в прямоугольник со сторонами параллельными главным осям рассеивания, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вероятность попадания в прямоугольник со сторонами параллельными главным осям рассеивания , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Пусть случайная точка 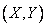 на плоскости подчинена нормальному закону

                                                (9.3.1)

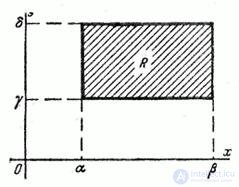
Рис. 9.3.1.

При этом главные оси рассеивания параллельны координатным осям и величины 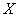 и 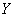 независимы.

 

Требуется вычислить вероятность попадания случайной точки 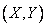 в прямоугольник 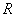, стороны которого параллельны координатным осям 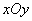, а, следовательно, и главным осям рассеивания (рис. Об этом говорит сайт https://intellect.icu . 9.3.1). Согласно общей формуле (8.3.4) имеем:

.

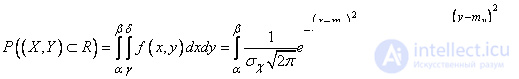откуда, применяя формулу (6.3.3) для вероятности попадания на участок, находим:

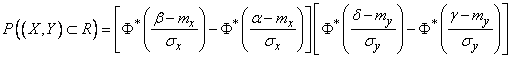,   (9.3.2)

где 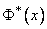 - нормальная функция распределения.

Если нормальный закон на плоскости дан в канонической форме, то 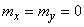, и формула (9.3.2) принимает вид

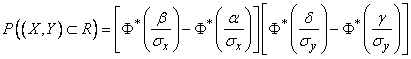.                (9.3.3)

Если стороны прямоугольника не параллельны координатным осям, то формулы (9.3.2) и (9.3.3) уже неприменимы. Только при круговом рассеивании вероятность попадания в прямоугольник любой ориентации вычисляется по формуле (9.3.2) или (9.3.3).

Формулы (9.3.2) и (9.3.3) широко применяются при вычислении вероятностей попадания в цели: прямоугольные, близкие к прямоугольным, составленные из прямоугольников или приближенно заменяемые таковыми.

Пример. Производится стрельба с самолета по прямоугольному щиту размером 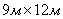 лежащему на земле горизонтально. Главные вероятные отклонения: в продольном направлении 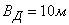, в боковом направлении 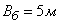. Прицеливание – по центру мишени, заход – вдоль мишени. Вследствие несовпадения дальности пристрелки и дальности  фактической стрельбы средняя точка попадания смещается в сторону недолета на 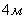. Найти вероятность попадания в мишень при одном выстреле.

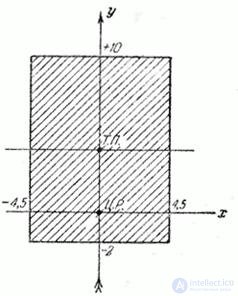
Рис. 9.3.2.

Решение. На чертеже (рис. 9.3.2) наносим мишень, точку прицеливания (т.п.) и центр рассеивания (ц.р.). Через ц.р. проводим главные оси рассеивания: по направлению полета и перпендикулярно к нему.

Перейдем от главных вероятных отклонени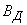й  и 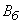 к главным средним квадратическим:

.

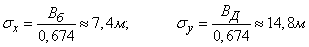По формуле (9.3.3) имеем:

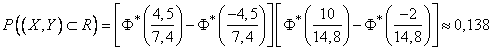
Информация, изложенная в данной статье про вероятность попадания в прямоугольник со сторонами параллельными главным осям рассеивания , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое вероятность попадания в прямоугольник со сторонами параллельными главным осям рассеивания и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про вероятность попадания в прямоугольник со сторонами параллельными главным осям рассеивания