Парадокс Бертрана (вероятность)

Привет, сегодня поговорим про парадокс бертрана вероятность , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое парадокс бертрана вероятность , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Парадокс Бертрана — проблема классического определения теории вероятностей. Жозеф Бертран описал парадокс в своей работе Calcul des probabilités (1888) в качестве примера того, что вероятность не может быть четко определена, пока не определен механизм или метод выбора случайной величины ^[1].

Формулировка Бертрана[править ]

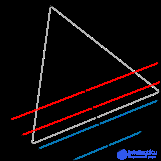
Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника?

Бертран предложил три решения, очевидно верных, но дающих различный результат.

1. 

   Случайные хорды, выбранные по методу 1; красные — длиннее стороны треугольника, синие — короче
   Метод «случайных концов»: наудачу выберем две точки на окружности и проведем через них хорду. Чтобы посчитать искомую вероятность, представим, что треугольник повернут так, что одна из его вершин совпадает с концом хорды. Заметим, что если другой конец хорды лежит на дуге между двумя другими вершинами треугольника, то длина хорды больше стороны треугольника. Длина рассмотренной дуги равна трети длины окружности, следуя классическому определению, искомая вероятность равна .
2. 

   Случайные хорды, выбранные по методу 2
   Метод «случайного радиуса»: зафиксируем радиус окружности, наудачу выберем точку на радиусе. Построим хорду, перпендикулярную зафиксированному радиусу, проходящую через выбранную точку. Для нахождения искомой вероятности, представим, что треугольник повернут так, что одна из его сторон перпендикулярна зафиксированному радиусу. Хорда длиннее стороны треугольника, если ее центр ближе к центру, чем точка пересечения треугольника с зафиксированным радиусом. Сторона треугольника делит пополам радиус, следовательно вероятность выбрать хорду длиннее стороны треугольника .
3. 

   Случайные хорды, выбранные по методу 3
   Метод «случайного центра»: выберем наудачу произвольную точку внутри круга и построим хорду с центром в выбранной точке. Об этом говорит сайт https://intellect.icu . Хорда длиннее стороны равностороннего треугольника, если выбранная точка находится внутри круга, вписанного в треугольник. Площадь вписанного круга есть 1/4 от площади большего, значит исходная вероятность равна .
   
   

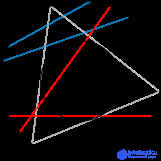
Выбор метода также может быть изображен следующим образом. Хорда однозначно задается ее серединой. Все три метода, описанные выше, дают различное, каждый свое, распределение середины. Методы 1 и 2 представляют два разных неравномерных распределения, в то время как третий метод дает равномерное распределение. С другой стороны, если посмотреть на изображения хорд ниже, то заметно, что хорды в методе 2 дают равномерно закрашенный круг, а 1-й и 3-й методы не дают такой картины.

Срединные точки хорд, выбранные случайным образом. Метод 1	Срединные точки хорд, выбранные случайным образом. Метод 2	Срединные точки хорд, выбранные случайным образом. Метод 3
Хорды, выбранные случайным образом. Метод 1	Хорды, выбранные случайным образом. Метод 2	Хорды, выбранные случайным образом. Метод 3

Могут быть придуманы и другие распределения; многие из них дадут разные доли хорд, имеющих большую длину, чем сторона вписанного треугольника.

Классическое решение[править ]

Классическое решение проблемы, таким образом, зависит от метода, которым случайно выбрана хорда. Тогда и только тогда, когда метод случайного выбора задан, проблема имеет четко определенное решение. Метод отбора не уникален, поэтому не может быть единственного решения. Три решения, представленные Бертраном, соответствуют различным методам отбора, и в отсутствие дополнительной информации нет оснований предпочесть какой-либо один.

Этот и другие парадоксы классического определения вероятности оправдывают более строгие формулировки, включающие частотные вероятности и субъективныеБайесовские вероятности.

Решение Джейнса с использованием принципа неопределенности[править ]

Эдвин Джейнс в своей работе 1973 года «Корректно поставленная проблема»^[2] предложил решение парадокса Бертрана, основанное на принципе неопределенности: мы не должны использовать информацию, которая не дана в условии. Джейнс указал, что проблема Бертрана не задает положение или размер круга, и утверждал, что в таком случае любые точные и объективные решения должны быть «безразличны» к размеру и положению. Иными словами, решение должно быть инвариантно к размерам и трансформациям.

Для иллюстрации: допустим, хорды случайно лежат в круге с диаметром 2 (скажем, после того как в круг с расстояния были брошены соломинки). Затем другой круг с меньшим диаметром (например, 1.1) накладывается на большой. Теперь распределение хорд в меньшем круге должно быть таким же, как и в большем. Если перемещать меньший круг по большему, вероятность не должна меняться. Это должно быть наглядно выражено в случае изменений в методе 3: распределение хорд в маленьком круге может выглядеть качественно другим, нежели их распределение в большом круге.

 

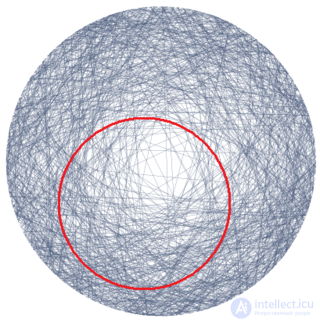
Та же ситуация с методом 1, хотя она более сложна в графическом изображении. Единственно метод 2 инвариантен как размерно, так и трансформационно, метод 3 имеет только размерную инвариантность, метод 1 — ни одной.

Однако Джейнс использовал не только инвариантность для принятия или отвержения данных методов: это означало бы то же самое, что оставить возможность существования еще не описанного метода, отвечающего критериям здравого смысла. Джэйнс использовал интегральные уравнения, описывая инвариантность, для точного определения вероятности распределения. Для данной задачи интегральные равенства действительно имеют единственное решение — то, что названо выше методом 2, методом случайного радиуса.

Физические эксперименты[править ]

Метод 2 — единственное решение, обладающее трансформационной инвариантностью, которая присутствует в определенных физических системах (таких так статистическая механика и физика газов), а также и в предлагаемом Джеймсом эксперименте со случайным бросанием соломинок с расстояния в круг. Тем не менее, кто-то может провести иные эксперименты, дающие результаты касательно других методов. Например, для того чтобы прийти к решению в методе 1, методе случайных концов, можно прикрепить вращатель в центр круга и позволить результатам двух независимых вращений отметить конечные точки хорд. Для того, чтобы прийти к решению в методе 3, нужно покрыть круг патокой и отметить первую точку, куда приземлится серединная точка хорды. Несколько наблюдателей разработали эксперименты для получения различных решений и верификации результатов опытным путем.^[3][4][5]

Надеюсь, эта статья про парадокс бертрана вероятность , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое парадокс бертрана вероятность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ