Лекция
Привет, сегодня поговорим про нормальное распределение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое нормальное распределение, распределение гаусса, примеры решения задач на распределение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
нормальное распределение , также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей сфункцией Гаусса:
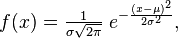
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в статье «Многомерное нормальное распределение».
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.
Плотность вероятности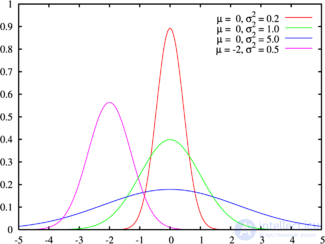 Зеленая линия соответствует стандартному нормальному распределению |
|
Функция распределения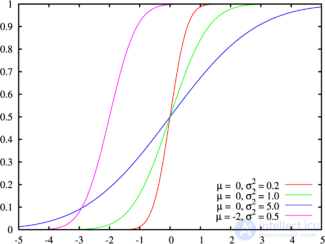 Цвета на этом графике соответствуют графику наверху |
|
| Обозначение | 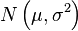 |
| Параметры | μ — коэффициент сдвига(вещественное число) σ > 0 — коэффициент масштаба(вещественный, строго положительный) |
| Носитель | 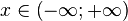 |
| Плотность вероятности | 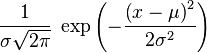 |
| Функция распределения | 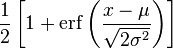 |
| Математическое ожидание | 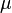 |
| Медиана | 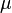 |
| Мода | 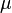 |
| Дисперсия | 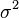 |
| Коэффициент асимметрии | 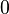 |
| Коэффициент эксцесса | 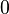 |
| Информационная энтропия | 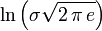 |
| Производящая функция моментов | 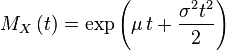 |
| Характеристическая функция | 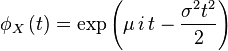 |
Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.
Моментами и абсолютными моментами случайной величины X называются математические ожидания X p и 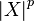 , соответственно. Если математическое ожидание случайной величины μ = 0, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целыхp.
, соответственно. Если математическое ожидание случайной величины μ = 0, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целыхp.
Если X имеет нормальное распределение, то для нее существуют (конечные) моменты при всех p с действительной частью больше −1. Для неотрицательных целых p, центральные моменты таковы:
![\mathrm{E}\left[X^p\right] =
\begin{cases}
0 & p=2n+1, \\
\sigma^p\,\left( p-1 \right)!! & p=2n.
\end{cases}](/th/25/blogs/id4299/17_c6afddd335aa40526a06f76ca7e0199f.png)
Здесь n — натуральное число, а запись (p − 1)!! означает двойной факториал числа p − 1, то есть (посколькуp − 1 в данном случае нечетно) произведение всех нечетных чисел от 1 до p − 1.
Центральные абсолютные моменты для неотрицательных целых p таковы:
![\operatorname{E}\left[\left|X\right|^p\right] =
\sigma^p\,\left(p-1\right)!! \cdot \left.\begin{cases}
\sqrt{\frac{2}{\pi}} & p=2n+1, \\
1 & p=2n.
\end{cases}\right\}
= \sigma^p \cdot \frac{2^{\frac{p}{2}}\Gamma\left(\frac{p+1}{2}\right)}{\sqrt{\pi}}.](/th/25/blogs/id4299/18_64dc5bfa366676ad675a9fa35b215bde.png)
Последняя формула справедлива также для произвольных p > −1.
Нормальное распределение является бесконечно делимым.
Если случайные величины 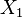 и
и 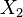 независимы и имеют нормальное распределение с математическими ожиданиями
независимы и имеют нормальное распределение с математическими ожиданиями 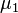 и
и 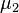 и дисперсиями
и дисперсиями 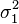 и
и 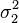 соответственно, то
соответственно, то 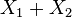 также имеет нормальное распределение с математическим ожиданием
также имеет нормальное распределение с математическим ожиданием 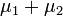 и дисперсией
и дисперсией  Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.
Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.
Нормальное распределение является непрерывным распределением с максимальной энтропией при заданном математическом ожидании и дисперсии.
Простейшие приближенные методы моделирования основываются на центральной предельной теореме. Об этом говорит сайт https://intellect.icu . Именно, если сложить несколько независимых одинаково распределенных величин с конечной дисперсией, то сумма будет распределена приблизительно нормально. Например, если сложить 100 независимых стандартноравномерно распределенных случайных величин, то распределение суммы будет приближенно стандартным нормальным.
Для программного генерирования нормально распределенных псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределенную величину на базе одной равномерно распределенной.
Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например, биномиальное и пуассоновское. Этим распределением моделируются многие не детерминированные физические процессы.
Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование свойств личности человека в психологии и психиатрии.
Из пункта 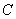 ведется стрельба из орудия вдоль прямой
ведется стрельба из орудия вдоль прямой 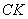 . Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадет с перелетом от 5 до 70м.
. Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадет с перелетом от 5 до 70м.
Классика жанра.
Решение: в задаче рассматривается нормально распределенная случайная величина 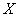 – дальность полета снаряда, и по условию
– дальность полета снаряда, и по условию 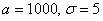 .
.
Так как речь идет о перелете за цель, то 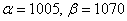 . Вычислим вероятность
. Вычислим вероятность 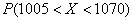 – того, что снаряд упадет в пределах этой дистанции.
– того, что снаряд упадет в пределах этой дистанции.
Если в нашем распоряжении есть таблица значений функции 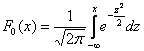 , то используем формулу
, то используем формулу 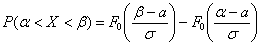 :
:
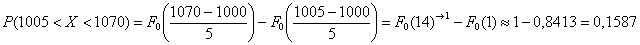
Для самопроверки можно задействовать экселевскую функцию =НОРМСТРАСП(z) или напрямую «забить» 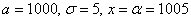 и затем
и затем 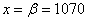 в Пункт 9 расчетного макета.
в Пункт 9 расчетного макета.
Если же в нашем распоряжении есть таблица значений функции Лапласа 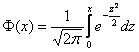 , то решаем через нее:
, то решаем через нее:
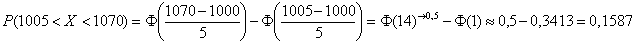
Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.
Напоминаю, что 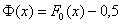 , и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.
, и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.
Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:
– с перелетом от 5 до 70 м упадет примерно 15,87% снарядов
Тренируемся самостоятельно:
Пример 3
Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.
В образце решения и далее я буду использовать функцию Лапласа, как самый распространенный вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.
И уже в этом примере нам встретился особый случай – когда интервал 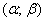 симметричен относительно математического ожидания. В такой ситуации его можно записать в виде
симметричен относительно математического ожидания. В такой ситуации его можно записать в виде 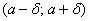 и, пользуясь нечетностью функции Лапласа, упростить рабочую формулу:
и, пользуясь нечетностью функции Лапласа, упростить рабочую формулу:
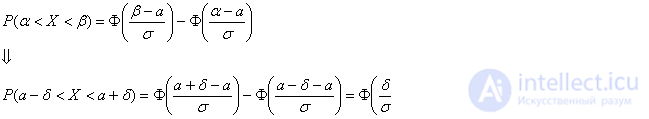
Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство можно «упаковывать» с помощью модуля:
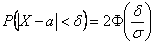 – вероятность того, что значение случайной величины
– вероятность того, что значение случайной величины 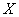 отклонится от математического ожидания менее чем на
отклонится от математического ожидания менее чем на 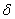 .
.
Хорошо то решение, которое умещается в одну строчку:)
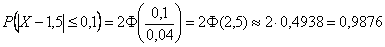 – вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
Результат этой задачи получился близким к единице, но хотелось бы еще бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счет? Существует! На поставленный вопрос отвечает так называемое
Его суть состоит в том, что практически достоверным является тот факт, что нормально распределенная случайная величина 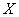 примет значение из промежутка
примет значение из промежутка 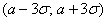 .
.
И в самом деле, вероятность отклонения от матожидания менее чем на 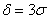 составляет:
составляет:
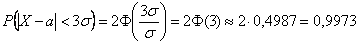 или 99,73%
или 99,73%
В «пересчете на подшипники» – это 9973 штуки с диаметром от 1,38 до 1,62 см и всего лишь 27 «некондиционных» экземпляров.
В практических исследованиях правило «трех сигм» обычно применяют в обратном направлении: если статистически установлено, что почти все значения исследуемой случайной величины укладываются в интервал длиной 6 стандартных отклонений, то появляются веские основания полагать, что эта величина распределена по нормальному закону. Проверка осуществляется с помощью теории статистических гипотез.
Продолжаем решать суровые советские задачи:
Пример 4
Случайная величина 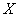 ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.
ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.
Решение очень простое. По условию, 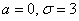 и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение
и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение 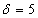 и по формуле
и по формуле 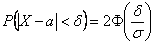 :
:
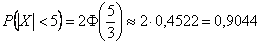 – вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
Ответ: 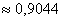
Прорешанная задача принципиально отличается от вроде бы похожего Примера 3 урока о равномерном распределении. Там была погрешность округления результатов измерений, здесь же речь идет о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине экспериментатора – когда мы, например, «на глазок» снимаем показания со стрелки тех же весов.
Помимо прочих, существуют еще так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно «прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически ведь можно обсчитать. Однако, в любом случае, случайной такая ошибка не будет, и ее матожидание отлично от нуля.
…срочно разрабатываю курс по подготовке продавцов =)
Самостоятельно решаем обратную задачу:
Пример 5
Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно 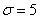 мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью
мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 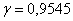 попадет длина диаметра валика.
попадет длина диаметра валика.
Пункт 5* расчетного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.
И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:
Пример 6
Нормально распределенная случайная величина 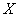 задана своими параметрами
задана своими параметрами 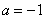 (математическое ожидание) и
(математическое ожидание) и 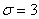 (среднее квадратическое отклонение). Требуется:
(среднее квадратическое отклонение). Требуется:
а) записать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что 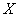 примет значение из интервала
примет значение из интервала 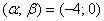 ;
;
в) найти вероятность того, что 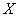 отклонится по модулю от
отклонится по модулю от 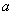 не более чем на
не более чем на 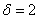 ;
;
г) применяя правило «трех сигм», найти значения случайной величины 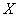 .
.
Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц ;)
Ну а я разберу пример повышенной сложности:
Пример 7
Плотность распределения вероятностей случайной величины 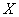 имеет вид
имеет вид 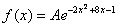 . Найти
. Найти 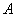 , математическое ожидание
, математическое ожидание 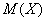 , дисперсию
, дисперсию 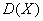 , функцию распределения
, функцию распределения 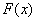 , построить графики плотности и функции распределения, найти
, построить графики плотности и функции распределения, найти 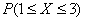 .
.
Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по себе присутствие экспоненты еще ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения еще нужно обосновать:
Так как функция 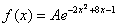 определена при любом действительном значении
определена при любом действительном значении 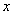 , и ее можно привести к виду
, и ее можно привести к виду 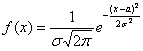 , то случайная величина
, то случайная величина 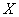 распределена по нормальному закону.
распределена по нормальному закону.
Приводим. Для этого выделяем полный квадрат и организуем трехэтажную дробь:
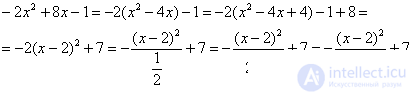
Обязательно выполняем проверку, возвращая показатель в исходный вид:
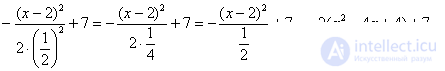
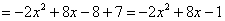 , что мы и хотели увидеть.
, что мы и хотели увидеть.
Таким образом:
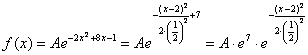 – по правилу действий со степенями «отщипываем»
– по правилу действий со степенями «отщипываем» 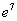 . И здесь можно сразу записать очевидные числовые характеристики:
. И здесь можно сразу записать очевидные числовые характеристики:
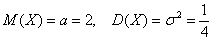
Теперь найдем значение параметра 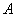 . Поскольку множитель нормального распределения имеет вид
. Поскольку множитель нормального распределения имеет вид 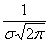 и
и 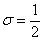 , то:
, то:
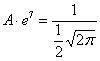 , откуда выражаем
, откуда выражаем 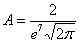 и подставляем в нашу функцию:
и подставляем в нашу функцию:
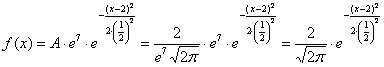 , после чего еще раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид
, после чего еще раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид 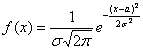 .
.
Построим график плотности:
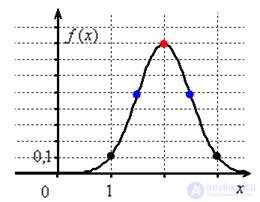
и график функции распределения 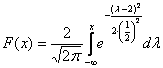 :
:
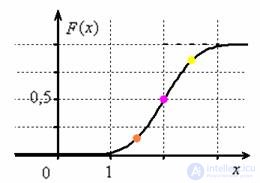
Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке 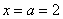 функция распределения принимает значение
функция распределения принимает значение 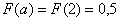 и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти еще хотя бы пару точек. Берем традиционное значение
и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти еще хотя бы пару точек. Берем традиционное значение 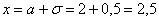 и стандартизируем его по формуле
и стандартизируем его по формуле 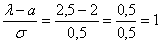 . Далее с помощью таблицы значений функции Лапласа находим:
. Далее с помощью таблицы значений функции Лапласа находим: 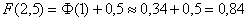 – желтая точка на чертеже. С симметричной оранжевой точкой никаких проблем:
– желтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: 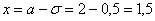 и:
и:
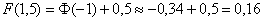 .
.
После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.
Да, и еще нужно вычислить:
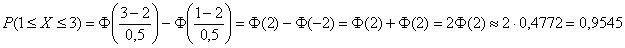 – вероятность того, что случайная величина
– вероятность того, что случайная величина 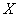 примет значение из данного отрезка.
примет значение из данного отрезка.
Ответ: 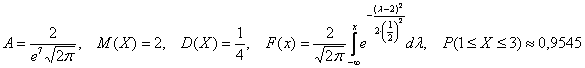
На этом все! Теперь вы знаете все про нормальное распределение, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое нормальное распределение, распределение гаусса, примеры решения задач на распределение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ