Лекция
Сразу хочу сказать, что здесь никакой воды про теорема, и только нужная информация. Для того чтобы лучше понимать что такое теорема, аксиома, лемма, следствия, аксиоматизация теории , настоятельно рекомендую прочитать все из категории введение в математику. основы. Кликните на вариант (или варианты ответов), если он правильный - то будет подсвечен зеленым цветом и вам будет зачислено пару монеток, а если неверный - то красным и будет снята монетка. Удачи в прохождении онлайн теста!
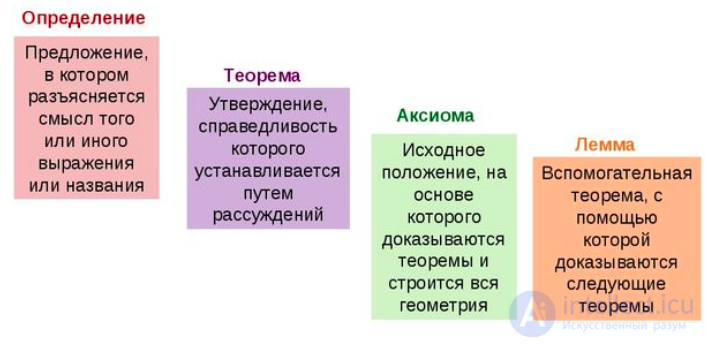
В математических дисциплинах широко используются четкие понятия такие как определения, теоремы, леммы, аксиомы, расссмотрим что это такое?
теорема (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем, аксиома ми называются утверждения, которые в рамках конкретной теории принимаются истинными без всяких доказательств или обоснований.
В математических текстах теоремами обычно называют только те доказанные утверждения, которые находят широкое применение в решении математических задач. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределенные утверждения). Менее важные утверждения-теоремы обычно называют лемма ми,предложениями, следствия ми, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называютгипотезами.
Наиболее знаменитыми являются теоремы Ферма, Пифагора и Птолемея.
Лемма (греч. λημμα — предположение) — доказанное утверждение, полезное не само по себе, а для доказательства других утверждений. Примеры известных лемм —лемма Евклида, лемма Жордана, лемма Гаусса, лемма Накаямы, лемма Гриндлингера, Лемма Лоренца, Лемма Лебедева.
Аксиома (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое в основе доказательства других ее положений.
Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.
В современной науке аксиомы — это те положения теории, которые принимаются за исходные, причем вопрос об истинности решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.
Аксиоматизация теории — явное указание конечного или счетного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. Об этом говорит сайт https://intellect.icu . После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, все дальнейшее изложение должно основываться исключительно лишь на этих аксиомах, не опираясь на обычное конкретное значение этих объектов и их отношений. Утверждения на основе аксиом называются теоремами.
Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и Евклидовой геометрии.
Набор аксиом называется непротиворечивым, если из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание. Аксиомы являются своего рода «точками отсчета» для построения теорий в любой науке, при этом сами они не доказываются, а выводятся непосредственно из эмпирического наблюдения (опыта) или обосновываются в более глубокой теории.
Австрийский математик Курт Гедель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система) начиная с определенного уровня сложности либо внутренне противоречива, либо неполна (то есть в достаточно сложных системах найдется хотя бы одно высказывание, истинность и ложность которого не может быть доказана средствами самой этой системы).
Примеры аксиом

Следствие — утверждение, которое выводится непосредственно из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Приведем примеры следствий из аксиомы о параллельности прямых:
Впервые термин «аксиома» встречается у Аристотеля (384—322 до н. э.) и перешел в математику от философов Древней Греции. Евклид различает понятия «постулат» и «аксиома», не объясняя их различия. Со времен Боэция постулаты переводят как требования (petitio), аксиомы — как общие понятия. Первоначально слово «аксиома» имело значение «истина, очевидная сама по себе». В разных манускриптах Начал Евклида разбиение утверждений на аксиомы и постулаты различно, не совпадает их порядок. Вероятно переписчики придерживались разных воззрений на различие этих понятий.
Отношение к аксиомам как к неким неизменным самоочевидным истинам сохранялось долгое время. Например, в словаре Даля аксиома — это «очевидность, ясная по себе и бесспорная истина, не требующая доказательств».
Сейчас аксиомы обосновываются не сами по себе, а в качестве необходимых базовых элементов теории. Критерии формирования набора аксиом в рамках конкретной теории часто являются прагматическими: краткость формулировки, удобство манипулирования, минимизация числа исходных понятий и т. п. Такой подход не гарантирует истинность принятых аксиом. Лишь подтверждение теории является одновременно и подтверждением набора ее аксиом.
Подведем итог и сделам сравнения и выявим сходства и различия
1. Правило, которое принимается без доказательств.
2. Утверждение доказано с помощью аксиом, постулатов или других теорем, которые заведомо верны это
3.Математическое утверждение, требующее доказательства, - это
4.Математическое утверждение, которое НЕ требует доказательства, является
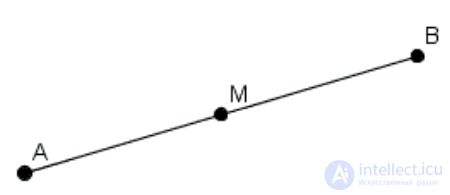
5.Если AB = 10, какое определение объясняет, почему AM = 5?
6. доказанное утверждение испольуемое для доказательства других утверждений
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про теорема Надеюсь, что теперь ты понял что такое теорема, аксиома, лемма, следствия, аксиоматизация теории и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы
Из статьи мы узнали кратко, но содержательно про теорема
Комментарии
Оставить комментарий
введение в математику. основы
Термины: введение в математику. основы