Сразу хочу сказать, что здесь никакой воды про открытые математические проблемы, и только нужная информация. Для того чтобы лучше понимать что такое
открытые математические проблемы, нерешенные проблемы , настоятельно рекомендую прочитать все из категории введение в математику. основы.
Открытые (нерешенные) математические проблемы — задачи, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве.
В научном мире популярна практика составления известными учеными или организациями списков открытых проблем, актуальных на текущий момент. В частности, известными списками математических проблем являются:
- Проблемы Гильберта
- Проблемы Ландау
- Проблемы тысячелетия
- Проблемы Смейла
Со временем опубликованные проблемы из такого списка могут быть решены и, таким образом, потерять статус открытых. Например, часть проблем Гильберта, представленных им в 1900 году, на данный момент так или иначе решены.
кто платит за их решение? ответ прост - энтузиазм и способность достижения поставленных целей - это духовное наставничесто, а материальная оплата- это разные фонды и общества, которые выделяют вознаграждения на поиск решения подобных проблем.
Теория чисел
Открытые проблемы в теории чисел
- Проблема Гольдбаха. Каждое ли четное число, большее 2, можно представить в виде суммы двух простых чисел?
- Проблема Варинга. Функция Харди
 — наименьшее
— наименьшее  такое, что уравнение
такое, что уравнение  разрешимо при
разрешимо при  . Значения этой функции известны только для
. Значения этой функции известны только для  равных 2 и 4.
равных 2 и 4.
- Бесконечно ли множество простых чисел-близнецов?
- Гипотеза Биля. Верно ли, что если
 где
где 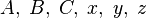 — натуральные и
— натуральные и  , то
, то  имеют общий простой делитель?
имеют общий простой делитель?
- Гипотеза Коллатца (гипотеза 3n+1).
- Гипотеза Эрдеша. Верно ли, что если сумма обратных величин для некоторого множества натуральных чисел расходится, то в этом множестве можно найти сколь угодно длинные арифметические прогрессии?
- Числа ван дер Вардена (англ.). При каком наименьшем N при любом разбиении множества
 на два подмножества хотя бы одно из них будет содержать арифметическую прогрессию длиной 7?
на два подмножества хотя бы одно из них будет содержать арифметическую прогрессию длиной 7?
Гипотеза о числах-близнецах

Числа-близнецы
Близнецами называются такие простые числа, которые отличаются всего на 2. Например, 11 и 13, а также 5 и 3 или 599 и 601. Если бесконечность ряда простых чисел была доказана множество раз начиная с античности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, среди простых чисел нет четных, а начиная с 3 — делящихся на три. Соответственно, если вычесть из ряда все, подходящие под "правила деления", то количество возможных близнецов становится все меньше. Единственный модуль для формулы нахождения таких чисел — 6, а формула выглядит следующим образом: 6n±1.
Гипотеза Коллатца
Другие названия: гипотеза 3n+1, сиракузская проблема, числа-градины. Если взять любое натуральное число n и совершить с ним следующие преобразования, рано или поздно всегда получится единица. Четное n нужно разделить надвое, а нечетное — умножить на 3 и прибавить единицу. Для числа 3 последовательность будет такой: 3×3+1=10, 10:2=5, 5×3+1=16, 16:2=8, 8:2=4, 4:2=2, 2:2=1. Очевидно, что если продолжить преобразование с единицы, то начнется цикл 1,4,2. Достаточно быстро количество шагов в вычислениях начинает превышать сто и на решение каждой новой последовательности требуется все больше ресурсов.
Проблема Гольдбаха (бинарная)
Еще одна задачка, формулировка которой выглядит проще пареной репы — любое четное число (больше 2) можно представить в виде суммы двух простых. И это краеугольный камень современной математики. Данное утверждение легко проверяется в уме для небольших значений: 18=13+5, 42=23+19. Причем рассматривая последнее, можно достаточно быстро понять всю глубину проблемы, ведь 42 представляется и как 37+5 и 11+31, а еще как 13+29 и 19+23. Для чисел больше тысячи количество пар слагаемых становится просто огромным. Это очень важно в криптографии, но даже самые мощные суперкомпьютеры не могут перебирать все значения до бесконечности, поэтому нужно какое-то четкое доказательство для всех натуральных чисел.
Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: «каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел»
Геометрия
- В задаче о перемещении дивана не доказана максимальность наилучшей оценки снизу (константы Гервера).
- На любой ли замкнутой кривой Жордана на плоскости можно найти 4 точки, являющиеся вершинами некоторого квадрата?
- Существует ли такая константа
 , что любое множество точек на плоскости, имеющее площадь
, что любое множество точек на плоскости, имеющее площадь  , обязательно содержит вершины хотя бы одного треугольникаплощадью 1?
, обязательно содержит вершины хотя бы одного треугольникаплощадью 1?
- Существует ли плотное множество точек на плоскости, расстояние между каждыми двумя точками которого рационально?
- Существует ли треугольник с целочисленными сторонами, медианами и площадью?
- Найдется ли в единичном квадрате точка, расстояние от которой до каждой из 4 вершин рационально?
- Задача о 9 кругах. Существует ли 9 кругов, таких, что каждые два пересекаются, и центр каждого круга лежит вне остальных кругов? (Время выполнения проверочного алгоритма — слишком большое).
- У любого ли выпуклого многогранника существует развертка без самопересечений?
- Даны положительные действительные числа
 . Какой наибольший и наименьший объем может иметь многогранник, площади граней которого равны этим числам?
. Какой наибольший и наименьший объем может иметь многогранник, площади граней которого равны этим числам?
- Во сколько раз объем невыпуклого многогранника может превосходить объем выпуклого многогранника, составленного из тех же граней?[10]
- При каком минимальном
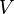 любое выпуклое тело единичного объема можно поместить внутри какой-либо треугольной пирамиды объема
любое выпуклое тело единичного объема можно поместить внутри какой-либо треугольной пирамиды объема  [11]
[11]
- Чему равно хроматическое число
 -мерного евклидового пространства? Эта задача не решена даже для плоскости. Другими словами, неизвестно, какое минимальное количество цветов нужно, чтобы ими можно было раскрасить плоскость так, чтобы никакие две точки, находящиеся на единичном расстоянии друг от друга, не были выкрашены в один и тот же цвет (Проблема Нелсона — Эрдеша — Хадвигера).
-мерного евклидового пространства? Эта задача не решена даже для плоскости. Другими словами, неизвестно, какое минимальное количество цветов нужно, чтобы ими можно было раскрасить плоскость так, чтобы никакие две точки, находящиеся на единичном расстоянии друг от друга, не были выкрашены в один и тот же цвет (Проблема Нелсона — Эрдеша — Хадвигера).
- Задача Томсона. Как разместить
 одинаковых заряженных точек на сфере, чтобы потенциальная энергия системы (то есть сумма попарных обратных расстояний между точками) была минимальна (задача строго решена только для
одинаковых заряженных точек на сфере, чтобы потенциальная энергия системы (то есть сумма попарных обратных расстояний между точками) была минимальна (задача строго решена только для 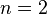 , 3, 4, 6 и 12).[12] Сколько состояний равновесия (локальных экстремумов) существует для системы из
, 3, 4, 6 и 12).[12] Сколько состояний равновесия (локальных экстремумов) существует для системы из  точек?
точек?
- Как разместить
 точек на сфере, чтобы наименьшее из попарных расстояний между ними было максимальным?[13]
точек на сфере, чтобы наименьшее из попарных расстояний между ними было максимальным?[13]
- Для каждой пары натуральных чисел (n, k) найти такое наименьшее действительное число d(n, k), что любое множество единичного диаметра в n-мерном евклидовом пространстве можно разбить на k подмножеств диаметром не больше d(n, k). Задача решена только в нескольких частных случаях.[14][15]
- Чему равна площадь множества Мандельброта? Существует оценка 1,506 591 77 ± 0,000 000 08.[16]
- Задача со счастливым концом. При каком минимальном
 среди любых
среди любых  точек на плоскости, никакие 3 из которых не лежат на одной прямой, найдутся вершины некоторого выпуклого
точек на плоскости, никакие 3 из которых не лежат на одной прямой, найдутся вершины некоторого выпуклого  -угольника? Решение известно только для
-угольника? Решение известно только для  . Результат для
. Результат для 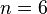 (который оказался равен 17) получен в 2006 году с помощью компьютерного анализа.
(который оказался равен 17) получен в 2006 году с помощью компьютерного анализа.
- Какое наименьшее количество плиток может содержать множество плиток Ванга (англ.), которым можно замостить плоскость только непериодически? Наименьший известный результат — 13.
- В любой ли многоугольной комнате с зеркальными стенами существует точка, при размещении в которой источника света вся комната окажется освещенной?[17]
- Можно ли разместить 8 точек на плоскости так, чтобы никакие 3 из них не лежали на одной прямой, никакие 4 не лежали на одной окружности и расстояние между любыми 2 точками было целым числом? Решение для 7 точек было найдено в 2007 году.[18][19][20]
- Каков наибольший возможный объем выпуклой оболочки пространственной кривой длины 1?
- Гипотеза Боннесена — Фенхеля. Какое трехмерное тело постоянной ширины имеет наименьший объем?[21][22][23]
Задачи упаковки
- Какое наибольшее количество непересекающихся окружностей единичного радиуса можно разместить на сфере радиуса
 ?[24]
?[24]
- Чему равна сторона наименьшего квадрата, в который можно упаковать 2 единичных круга, один из которых разрешается разрезать по хорде на 2 сегмента?[25]
- Какова наименее плотная жесткая упаковка одинаковых кругов на плоскости?
Проблема плотной упаковки равных сфер

Проблема плотной упаковки равных сфер
Это даже не одна, а целая категория схожих проблем. Об этом говорит сайт https://intellect.icu . Причем мы сталкиваемся с ними ежедневно, например, когда хотим разложить фрукты на полке в холодильнике или как можно плотнее расставить бутылки на полке. С математической точки зрения необходимо найти среднее количество контактов ("поцелуев", также называется контактным числом) каждой сферы с остальными. На данный момент есть точные решения для размерностей 1-4 и 8.
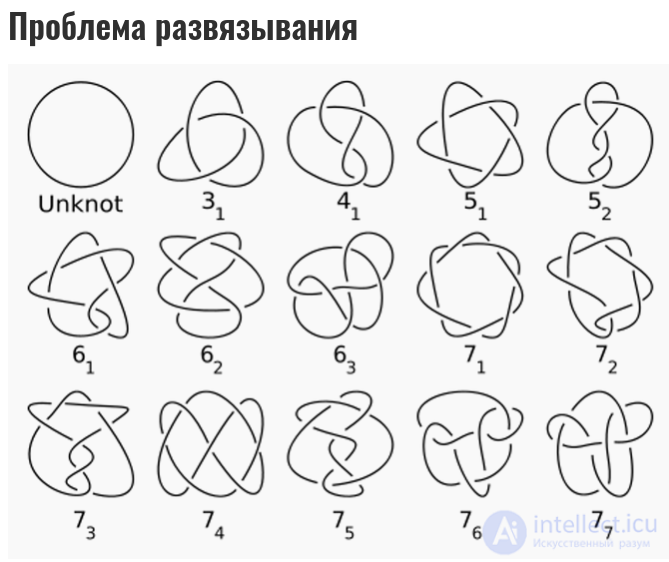
Проблема развязывания
И снова каждый день встречающаяся проблема. Казалось бы, что сложного — узел развязать? Тем не менее, вычисление минимального времени, необходимого для этой задачи является еще одним краеугольным камнем математики. Трудность в том, что мы знаем, вычислить алгоритм развязывания можно, но его сложность может быть такой, что даже самый мощный суперкомпьютер будет считать слишком долго.
Многомерные пространства
- Чему равно контактное число в евклидовых пространствах с размерностью
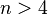 ? Эта задача решена лишь для
? Эта задача решена лишь для 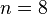 (240) и
(240) и 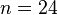 (196 560).[26][27]
(196 560).[26][27]
- Задача плотнейшей упаковки шаров в
 -мерном евклидовом пространстве для
-мерном евклидовом пространстве для 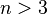 . Для трехмерного пространства эта задача была решена в 1998 году: было доказано, что гипотеза Кеплера справедлива. Однако, существующее доказательство чрезвычайно велико и сложно для проверки.[28]
. Для трехмерного пространства эта задача была решена в 1998 году: было доказано, что гипотеза Кеплера справедлива. Однако, существующее доказательство чрезвычайно велико и сложно для проверки.[28]
- Гипотеза Келлера. Можно ли заполнить 7-мерное пространство равными 7-мерными гиперкубами так, чтобы никакие два гиперкуба не имели целой общей 6-мерной гиперграни? (Известно, что для пространств размерности меньше 7 ответ отрицателен, а больше 7 — положителен)[29]
Механика
- Для каждого ли движения четырех точек в пространстве можно выбрать такую (возможно, неинерциальную) систему отсчета, чтобы в ней траектории всех четырех точек оказались плоскими выпуклыми кривыми?
- Верно ли, что при достаточно большом количестве движущихся точек с зацепленными траекториями (траектории называются зацепленными, если не существуетгомеоморфизма пространства, при котором они попадут внутрь непересекающихся выпуклых множеств) в любой системе отсчета траектории хотя бы двух точек окажутся зацепленными?
Алгебра
- Обратная теорема теории Галуа. Для любой конечной группы
 существует поле алгебраических чисел
существует поле алгебраических чисел 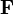 , такое что
, такое что 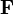 является расширением поля рациональных чисел
является расширением поля рациональных чисел 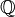 и
и  изоморфна
изоморфна  .
.
- Любая конечно заданная группа, каждый элемент которой имеет конечный порядок, — конечна. Для конечнопорожденной группы (более слабое условие) это неверно.[30]
- Существует ли простая группа, которая не является трансфинитно сверхпростой?
- Является ли кольцо периодов полем?
- Проблема О.Ю. Шмидта Существуют ли не квазициклические группы, все собственные подгруппы (подгруппы, отличные от единичной и всей группы) которых конечны?[32]
- Проблема Л.С. Понтрягина Пусть
 - эффективная транзитивная бикомпактная группа преобразований пространства
- эффективная транзитивная бикомпактная группа преобразований пространства  , гомеоморфного
, гомеоморфного  - мерной сфере. Существует ли такое гомеоморфное отображение пространства
- мерной сфере. Существует ли такое гомеоморфное отображение пространства  на единичную сферу
на единичную сферу  евклидова
евклидова  - мерного пространства, при котором группа
- мерного пространства, при котором группа  переходит в некоторую группу движений сферы
переходит в некоторую группу движений сферы  ?[33].
?[33].
- Алгебраические системы Существуют ли и каким условиям удовлетворяют в случае существования нетривиальные многообразия группоидов, колец и решеток, достижимых на классах всех группоидов, всех колец или решеток?.
- Алгебраические системы Существуют ли и каким условиям удовлетворяют в случае существования нетривиальные многообразия и квазимногообразия полугрупп c несколькими выделенными элементами, колец и решеток, достижимых на классе всех таких полугрупп.
- Существуют ли во множестве групп операции, отличные от операций прямого и свободного умножения и обладающие их основными свойствми?
- Будет ли множество всех неизоморфных абелевых групп данной мощности
 иметь мощность
иметь мощность  ?
?
- Проблема А. И. Мальцева Существует ли такая счетная группа, что всякая счетная группа изоморфна одной из ее подгрупп
Коуровская тетрадь
Представляет собой всемирно известный сборник нескольких тысяч нерешенных задач в области теории групп. Издается с 1965 года с периодичностью в 2-4 года. Выпускается на русском и английском языках.[38][39]
Днестровская тетрадь
Представляет собой сборник нескольких сотен нерешенных задач теории колец и модулей.
Свердловская тетрадь
Представляет собой сборник нерешенных задач теории полугрупп.
Анализ
- Гипотеза Римана. Все ли нетривиальные нули дзета-функции лежат на прямой
 ?
?
- Чему равна постоянная Миллса? Существующие методы вычисления опираются на еще недоказанную гипотезу Римана.
- До сих пор ничего не известно о нормальности таких чисел, как
 и
и  ; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа
; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа  бесконечное количество раз.
бесконечное количество раз.
- Является ли всякое иррациональное алгебраическое число нормальным?
- Является ли
 нормальным числом?
нормальным числом?
- Неизвестно ни одного числа, для которого было бы доказано, что среднее геометрическое членов его разложения в непрерывную дробь стремится к постоянной Хинчина (англ.), хотя и доказано, что этим свойством обладают почти все действительные числа. Предполагается, что этим свойством должны обладать числа
 ,Постоянная Эйлера — Маскерони, сама постоянная Хинчина и многие другие математические константы.
,Постоянная Эйлера — Маскерони, сама постоянная Хинчина и многие другие математические константы.
- Сходятся ли ряды
 и
и 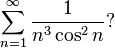
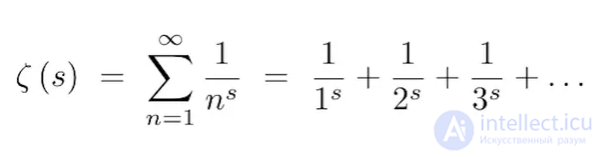
Гипотеза Римана
Если кратко, то Бернхард Риман предположил, что распределение простых чисел по множеству всех натуральных чисел не подчиняется каким-либо законам. Но их количество на заданном участке числового ряда коррелирует с распределением определенных значений на графике дзета-функции. Она расположена выше и для каждого s дает бесконечное количество слагаемых. Например, когда в качестве s подставляется 2, то в результате получается уже решенная “базельская задача” — ряд обратных квадратов (1 + 1/4 + 1/9 + 1/16 + …).
Вопросы иррациональности
- Неизвестна мера иррациональности ни для одного из следующих чисел: постоянная Эйлера — Маскерони, постоянная Каталана, постоянная Бруна, постоянная Миллса, постоянная Хинчина, числа
 Ни для одного из них не известно даже, является ли онорациональным числом, алгебраическим иррациональным или трансцендентным числом[44][45][46][47][48][49][50].
Ни для одного из них не известно даже, является ли онорациональным числом, алгебраическим иррациональным или трансцендентным числом[44][45][46][47][48][49][50].
- Неизвестно, являются ли
 и
и  алгебраически независимыми.
алгебраически независимыми.
- Неизвестно, являются ли
 или
или 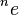 целыми числами при каком-либо положительном целом
целыми числами при каком-либо положительном целом  (см. тетрация). Неизвестно даже, является ли
(см. тетрация). Неизвестно даже, является ли  целым.
целым.
- Неизвестно, может ли
 быть целым, если
быть целым, если  — положительное целое число, а
— положительное целое число, а  — положительное рациональное, но не целое число (в частных случаях
— положительное рациональное, но не целое число (в частных случаях  ответ отрицателен).
ответ отрицателен).
- Неизвестно, является ли положительный корень уравнения
 алгебраическим или трансцендентным числом (хотя известно, что он иррационален).
алгебраическим или трансцендентным числом (хотя известно, что он иррационален).
- Неизвестно, является ли положительный корень уравнения
 рациональным, алгебраическим иррациональным или трансцендентным числом. Аналогичная проблема для тетрации любой большей высоты также открыта.
рациональным, алгебраическим иррациональным или трансцендентным числом. Аналогичная проблема для тетрации любой большей высоты также открыта.
- Неизвестна точная мера иррациональности для каждого из следующих иррациональных чисел:
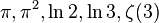 [52].
[52].
- Неизвестно, является ли первое число Скьюза
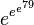 целым числом.
целым числом.
- Трансцендентны ли значения дзета-функции Римана
 для всех натуральных
для всех натуральных  ?
?
- Трансцендентны ли значения гамма-функции
 для всех целых
для всех целых 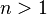 ?
?
- Трансцендентны ли постоянные Фейгенбаума?
- Трансцендентна ли постоянная Пелля?[53]
- Всякая ли бесконечная непериодическая непрерывная дробь с ограниченными членами — трансцендентна?
Комбинаторика
- Существование матрицы Адамара порядка, кратного 4.
- Существование конечной проективной плоскости натурального порядка, не являющегося степенью простого числа.
- Неизвестно количество незамкнутых маршрутов коня.
- Гипотеза Эрдеша - Реньи. Если
 - фиксированное целое число
- фиксированное целое число 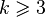 , то
, то 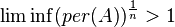 для
для  из
из  . Здесь
. Здесь 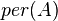 - перманент матрицы
- перманент матрицы  ,
,  - множество всех
- множество всех 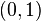 - матриц порядка
- матриц порядка  c
c  единицами в каждой строке и каждом столбце[54].
единицами в каждой строке и каждом столбце[54].
Теория графов
- Гипотеза Каццетты — Хаггвиста — ориентированный граф, имеющий n вершин, из каждой вершины которого выходит не менее m ребер, имеет замкнутый контур длиной не более
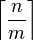 .[55]
.[55]
- Гипотеза Хадвигера — каждый n-хроматический граф стягиваем к полному графу
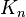 .
.
- Гипотеза Улама:
- а) всякий граф с более чем двумя вершинами однозначно определяется набором графов, где каждый граф из набора получен удалением одной из вершин исходного графа;
- б) всякий граф с более чем тремя вершинами однозначно определяется множеством графов, где каждый граф из множества получен удалением одной из вершин исходного графа.
- Гипотеза Харари (слабая форма гипотезы Улама) — если граф имеет более трех ребер, то его можно однозначно восстановить по подграфам, полученным удалением единственного ребра.
- В любом графе, не содержащем мостов (ребер, удаление которых увеличивает число компонент связности графа), можно выбрать множество простых циклов, такое, что каждое ребро принадлежит ровно двум из них.
- В любом кубическом графе можно выбрать 6 1-факторов так, чтобы каждое ребро принадлежало ровно двум из них.
Теория узлов
- Существует ли нетривиальный узел, полином Джонса которого является таким же, как и у тривиального узла?
- Чему равно количество простых узлов (англ.) с n двойными точками (англ.) для n > 16? Является ли эта последовательность строго возрастающей?[56] Значения дляn < 17 дает последовательность A002863 в OEIS.
Теория алгоритмов
Вопросы алгоритмической разрешимости
- Аналог 10-й проблемы Гильберта для уравнений степени 3: существует ли алгоритм, позволяющий по любому диофантовому уравнению степени 3 определить, имеет ли оно решения?
- Аналог 10-й проблемы Гильберта для уравнений в рациональных числах. Как узнать по произвольному диофантову уравнению, разрешимо ли оно в рациональных (не обязательно целых) числах и можно ли это узнать вообще (то есть возможен ли соответствующий алгоритм)?[57][58][59]
- Алгоритмическая разрешимость проблемы умирающей матрицы для матриц порядка 2. Существует ли алгоритм, позволяющий для данного конечного множества квадратных матриц
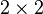 определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу.[60]
определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу.[60]
- Расширение класса выражений, для которых известен алгоритм, определяющий, равно ли выражение нулю (Проблема констант (англ.)). Для каких классов выражений эта задача алгоритмически неразрешима?
- Существует ли алгоритм, позволяющий узнать по целочисленной матрице, существует ли степень, имеющая нуль в правом верхнем углу?[59]
Теория сложности вычислений
- P = NP?
- Является ли задача изоморфизма графов NP-полной?[61]
- Принадлежит ли задача нахождения простого множителя натурального числа к классу P?
- Принадлежит ли задача распознавания тривиального узла (англ.) к классу P?
- Определить точную нижнюю границу сложности алгоритма умножения целых чисел. Из известных алгоритмов наименьшую сложность имеет алгоритм Мартина Фюрера, выполняющийся за
 , где
, где 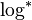 — итерированный логарифм (англ.).
— итерированный логарифм (англ.).
- Определить точную нижнюю границу сложности алгоритма умножения матриц. Из известных алгоритмов наименьшую сложность имеет алгоритм Копперсмита — Винограда, работающий за
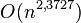 (однако с непрактично большим коэффициентом).
(однако с непрактично большим коэффициентом).
Другие проблемы теории алгоритмов
- Проблема «усердного бобра» (англ.)[62]. Сколько ходов может продержаться (незацикливающаяся) машина Тьюринга с
 состояниями и алфавитом
состояниями и алфавитом  на заполненной нулями ленте? Известно, что нет алгоритма (а значит, и рекурсивно аксиоматизируемой формальной теории), который может решить этот вопрос для всех
на заполненной нулями ленте? Известно, что нет алгоритма (а значит, и рекурсивно аксиоматизируемой формальной теории), который может решить этот вопрос для всех  , и пока известны только значения для
, и пока известны только значения для 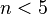 .[63]
.[63]
- Существует ли алгоритм, распознающий для любых двух трехмерных многообразий, заданных своими триангуляциями, гомеоморфны ли они?[59]
- Существует ли алгоритм, распознающий по произвольной позиции игры "Жизнь", "вымрет" ли она (станут ли в итоге все клетки пустыми)?[59]
- Существует ли теорема о полноте для решетки Мучника?[59]
- Существует ли алгоритм, определяющий разрешимость и арифметичность множества реализуемых и множества неопровержимых пропозициональных формул?[59]
- Существуют ли в обычных алгебраических системах алгебраически корректные массовые проблемы различной сложности?[59]
- Существует ли алгебраическая система, для которой равномерная эквивалентность отличается от программной или программная от проблемной?[59]
Аксиоматическая теория множеств
- В настоящее время наиболее распространенной аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для нее) остается нерешенным.
- Проблема Скулема. Рассмотрим множество
 функций одного натурального переменного
функций одного натурального переменного  , построенных из термов
, построенных из термов  и замкнутых относительно сложения,умножения и возведения в степень. Для функций
и замкнутых относительно сложения,умножения и возведения в степень. Для функций  из этого множества будем писать
из этого множества будем писать 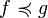 , если
, если 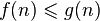 выполняется для всех достаточно больших
выполняется для всех достаточно больших  . Известно, что отношение
. Известно, что отношение  вполне упорядочивает множество
вполне упорядочивает множество  . Какой ординал соответствует этому упорядочению? (Известно, что он не меньше чем
. Какой ординал соответствует этому упорядочению? (Известно, что он не меньше чем  и не больше чем первый критический ординал
и не больше чем первый критический ординал  )[64][65] Аналогичные вопросы возникают при добавлении в множество разрешенных операторов дополненная тетрации,пентации и гипероператоров более высоких порядков (проблема Скулема, дополненная только тетрацией, была решена в 2010 году).[66][67]
)[64][65] Аналогичные вопросы возникают при добавлении в множество разрешенных операторов дополненная тетрации,пентации и гипероператоров более высоких порядков (проблема Скулема, дополненная только тетрацией, была решена в 2010 году).[66][67]
- Существует ли линейно упорядоченное множество с порядковым типом (англ.) α, удовлетворяющим условиям α ≠ α2 и α = α3?[68]
- В теории множеств Цермело-Френкеля без аксиомы выбора неизвестно, существуют ли регулярные кардиналы
 , большие
, большие  [69].
[69].
- Проблема сингулярных кардиналов. Для каких функций
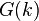 существует модель Цермело-Френкеля, в которой
существует модель Цермело-Френкеля, в которой 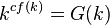 для всех кардиналов
для всех кардиналов  [70].
[70].
- Верно ли, что если непротиворечива система аксиом Цермело-Френкеля вместе с аксиомой выбора, то непротиворечива система аксиом Цермело-Френкеля, принцип зависимого выбора и каждое множество действительных чисел есть измеримое по Лебегу множество?[71]
- Не приведет ли к противоречию предположение существования таких кардинальных чисел
 , что декартово произведение m-компактных пространств всегда m-компактно. Неизвестно также, совпадало бы наименьшее из этих чисел с наименьшим измеримым числом или нет.
, что декартово произведение m-компактных пространств всегда m-компактно. Неизвестно также, совпадало бы наименьшее из этих чисел с наименьшим измеримым числом или нет.

Какая бесконечность самая большая? На первый взгляд бредовый вопрос, но так и есть — все бесконечности разные по размеру. А точнее, по мощности, ведь именно так различают множества чисел в математике. Под мощностью понимается общее количество элементов множества. Например, самая маленькая бесконечность — натуральные числа (1, 2, 3, ...), потому что она включает в себя только целые положительные числа. Ответа на этот вопрос пока нет и математики постоянно находят все более мощные множества.
Теория доказательств
- Какое самое короткое неразрешимое утверждение существует в арифметике Пеано?[73] Неразрешимое утверждение теории — это утверждение, которое невозможно ни доказать, ни опровергнуть в данной теории. Доказательства теорем Геделя демонстрируют, как можно строить такие утверждения, но получающиеся утверждения оказываются весьма значительного размера, будучи записанными на формальном языке арифметики.
Вычислительная математика
- Определить предельный уровень аппроксимации
 -стадийного метода Рунге — Кутты (одностадийный = метод Эйлера =
-стадийного метода Рунге — Кутты (одностадийный = метод Эйлера =  , двухстадийный =модифицированный метод Эйлера =
, двухстадийный =модифицированный метод Эйлера =  , четырехстадийный = классический метод Рунге — Кутты =
, четырехстадийный = классический метод Рунге — Кутты = 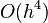 , пятистадийный = метод Фельберга (англ.) = тоже
, пятистадийный = метод Фельберга (англ.) = тоже 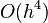 ).
).
Дифференциальные уравнения
- Неизвестно точное решение уравнения ван дер Поля (оно же осциллятор ван дер Поля):[74][75]
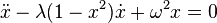
- Неизвестно точное решение уравнения Дуффинга [76]
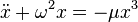
- Неизвестно точное решение уравнения Матье [77]
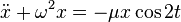
- Гипотеза Абловица-Рамани-Сегура Все обыкновенные дифференциальные уравнения, полученные из полностью интегрируемых дифференциальных уравнений в частных производных, обладают свойством Пенлеве (положение любой алгебраической, логарифмической или существенной особенности решений уравнения не зависит от начальных условий, от произвольных констант интегрирования зависит только положение полюсов)[78].
- Имеет ли гамильтонова система, интегрируемая по Лиувиллю, эквивалентную формулировку с помощью лаксовой пары, и если имеет, то как ее построить?[79]
Теория вероятностей
- Неизвестны необходимые и достаточные условия принадлежности безгранично делимого закона распределения случайной величины в одномерном и многомерном случаях к классу законов, не имеющих неразложимых компонент.[80]
Уравнения математической физики
- Отсутствует строгое математическое обоснование метода континуального интегрирования в квантовой теории поля[81].
- Континуальные интегралы удается вычислить только для случая гауссовых квадратур. В общем случае способ вычисления континуальных интегралов неизвестен[82].
- Неизвестно точное решение уравнения Шредингера для многоэлектронных атомов[83].
- В квантовой механике при решении задачи о рассеянии двух пучков на одном препятствии сечение рассеяния получается бесконечно большим[84]
- Уравнения Навье — Стокса
- В гидродинамике есть сотни нерешенных задач[85].
- Отсутствует законченная теория, объясняющая происхождение и эволюцию магнитного поля Земли[86].
Теория игр
- Отсутствует общая математическая теория игр, проводимых на пространстве функций (поскольку мощность множества действительных функций существенно превышает мощность континуума)[87].
- Отсутствует общая математическая теория псевдоигр (конфликтных ситуаций, не являющихся играми)[87].
- Отсутствует общая математическая теория некооперативных игр
 лиц для
лиц для  [87].
[87].
- Формулировки
 нерешенных проблем теории игр есть в книге [88].
нерешенных проблем теории игр есть в книге [88].
- Не решена задача построения алгоритмов обучения решению игр, когда элементы платежной матрицы не постоянны, а представляют собой случайные величины, либо неизвестны (игра вслепую)[89].
Теория представлений групп
- Гипотеза Ленглендса. Любое неприводимое представление вещественной полупростой группы Ли
 , входящее в дискретную часть разложения регулярного представления, реализуется в пространстве
, входящее в дискретную часть разложения регулярного представления, реализуется в пространстве  - когомологий подходящего пучка на пространстве
- когомологий подходящего пучка на пространстве  , где
, где  - компактная картановская подгруппа в
- компактная картановская подгруппа в  [90].
[90].
Общая топология
- Задача Даукера. Определить, является ли каждое нормальное хаусдорфово пространство счетно паракомпактным[91].
- Список из
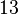 нерешенных проблем теоретико-множественной топологии есть в статье [92].
нерешенных проблем теоретико-множественной топологии есть в статье [92].
- Неизвестна мощность множеств, дополнительных к А-множествам, даже в одномерном случае[93].
Линейная алгебра
- Гипотеза Банаха. Всякое сепарабельное банахово пространство имеет счетный базис[94].
Теория случайных процессов
- Задача определения закона распределения
 числа выбросов случайного процесса в общем случае не имеет законченного и компактного решения[95].
числа выбросов случайного процесса в общем случае не имеет законченного и компактного решения[95].
- Задача определения закона распределения абсолютных максимумов случайного процесса решена только для марковских процессов. Для остальных процессов точное решение неизвестно[96].
Функциональный анализ
- Список из
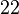 нерешенных задач теории операторов в банаховом пространстве есть в книге[97].
нерешенных задач теории операторов в банаховом пространстве есть в книге[97].
Теория динамических систем
- Неизвестно, является ли система из двух и более твердых биллиардных шаров К-потоком при несингулярных взаимодействиях[98].
Риманова геометрия
- Проблема Хопфа Существует ли на дифференцируемом многообразии
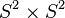 риманова метрика положительной кривизны?
риманова метрика положительной кривизны?
Исследование операций
- Не существует комбинаторного метода решения целочисленных задач линейного программирования с полиномиальной (в отличие от экспоненциальной) оценкой трудоемкости?
- Отсутствует общая теория алгоритмических методов оптимизации, позволяющая обеспечить ускорение сходимости и выбор шага итерации в общем случае многошаговых алгоритмов[101].
- Неизвестны условия сходимости почти наверное в область для многошаговых алгоритмов адаптации и обучения
- Неизвестны правила определения момента установления стационарности алгоритма адаптации и обучения
- Неизвестны оценки зависимости точности аппроксимации от числа функций и оценки времени обучения для алгоритмов опознавания
- Неизвестны общие способы получения несмещенных оценок при заданном критерии оптимальности в задачах идентификации
- Неизвестны общие правила выбора системы функций в задачах фильтрации.
- Неисследована связь между скоростью изменения внешних воздействий и длительностью процесса адаптации фильтра.
- Неизвестны способы использования априорной информации о распределениях случайных величин для построения адаптивных фильтров.
- Неизвестен способ применения адаптивного подхода при ускоренных испытаниях на надежность.
- Отсутствует общая теория сетевого планирования с применением адаптивного подхода при недостаточной априорной информации.
Известные проблемы, недавно решенные
- Проблема четырех красок
- Великая теорема Ферма
- Гипотеза Пуанкаре
- Гипотеза о раскраске дорог
- Гипотеза Ван дер Вардена о перманенте
- Гипотеза Такеути
- Гипотеза Бибербаха
- Проблема Серра
Вау!! 😲 Ты еще не читал? Это зря!
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про открытые математические проблемы Надеюсь, что теперь ты понял что такое открытые математические проблемы, нерешенные проблемы
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
введение в математику. основы
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
 — наименьшее
— наименьшее  такое, что уравнение
такое, что уравнение  разрешимо при
разрешимо при  . Значения этой функции известны только для
. Значения этой функции известны только для  равных 2 и 4.
равных 2 и 4. где
где 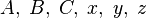 — натуральные и
— натуральные и  , то
, то  имеют общий простой делитель?
имеют общий простой делитель? на два подмножества хотя бы одно из них будет содержать арифметическую прогрессию длиной 7?
на два подмножества хотя бы одно из них будет содержать арифметическую прогрессию длиной 7? 

 , что любое множество точек на плоскости, имеющее площадь
, что любое множество точек на плоскости, имеющее площадь  , обязательно содержит вершины хотя бы одного треугольникаплощадью 1?
, обязательно содержит вершины хотя бы одного треугольникаплощадью 1?  . Какой наибольший и наименьший объем может иметь многогранник, площади граней которого равны этим числам?
. Какой наибольший и наименьший объем может иметь многогранник, площади граней которого равны этим числам?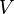 любое выпуклое тело единичного объема можно поместить внутри какой-либо треугольной пирамиды объема
любое выпуклое тело единичного объема можно поместить внутри какой-либо треугольной пирамиды объема  [11]
[11] -мерного евклидового пространства? Эта задача не решена даже для плоскости. Другими словами, неизвестно, какое минимальное количество цветов нужно, чтобы ими можно было раскрасить плоскость так, чтобы никакие две точки, находящиеся на единичном расстоянии друг от друга, не были выкрашены в один и тот же цвет (Проблема Нелсона — Эрдеша — Хадвигера).
-мерного евклидового пространства? Эта задача не решена даже для плоскости. Другими словами, неизвестно, какое минимальное количество цветов нужно, чтобы ими можно было раскрасить плоскость так, чтобы никакие две точки, находящиеся на единичном расстоянии друг от друга, не были выкрашены в один и тот же цвет (Проблема Нелсона — Эрдеша — Хадвигера). одинаковых заряженных точек на сфере, чтобы потенциальная энергия системы (то есть сумма попарных обратных расстояний между точками) была минимальна (задача строго решена только для
одинаковых заряженных точек на сфере, чтобы потенциальная энергия системы (то есть сумма попарных обратных расстояний между точками) была минимальна (задача строго решена только для 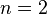 , 3, 4, 6 и 12).[12] Сколько состояний равновесия (локальных экстремумов) существует для системы из
, 3, 4, 6 и 12).[12] Сколько состояний равновесия (локальных экстремумов) существует для системы из  точек?
точек? точек на сфере, чтобы наименьшее из попарных расстояний между ними было максимальным?[13]
точек на сфере, чтобы наименьшее из попарных расстояний между ними было максимальным?[13] среди любых
среди любых  точек на плоскости, никакие 3 из которых не лежат на одной прямой, найдутся вершины некоторого выпуклого
точек на плоскости, никакие 3 из которых не лежат на одной прямой, найдутся вершины некоторого выпуклого  -угольника? Решение известно только для
-угольника? Решение известно только для  . Результат для
. Результат для 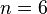 (который оказался равен 17) получен в 2006 году с помощью компьютерного анализа.
(который оказался равен 17) получен в 2006 году с помощью компьютерного анализа. ?[24]
?[24]

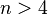 ? Эта задача решена лишь для
? Эта задача решена лишь для 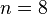 (240) и
(240) и 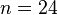 (196 560).[26][27]
(196 560).[26][27] -мерном евклидовом пространстве для
-мерном евклидовом пространстве для 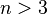 . Для трехмерного пространства эта задача была решена в 1998 году: было доказано, что гипотеза Кеплера справедлива. Однако, существующее доказательство чрезвычайно велико и сложно для проверки.[28]
. Для трехмерного пространства эта задача была решена в 1998 году: было доказано, что гипотеза Кеплера справедлива. Однако, существующее доказательство чрезвычайно велико и сложно для проверки.[28] существует поле алгебраических чисел
существует поле алгебраических чисел 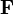 , такое что
, такое что  является расширением поля рациональных чисел
является расширением поля рациональных чисел  и
и  изоморфна
изоморфна  .
. - эффективная транзитивная бикомпактная группа преобразований пространства
- эффективная транзитивная бикомпактная группа преобразований пространства  , гомеоморфного
, гомеоморфного  - мерной сфере. Существует ли такое гомеоморфное отображение пространства
- мерной сфере. Существует ли такое гомеоморфное отображение пространства  на единичную сферу
на единичную сферу  евклидова
евклидова  - мерного пространства, при котором группа
- мерного пространства, при котором группа  переходит в некоторую группу движений сферы
переходит в некоторую группу движений сферы  ?[33].
?[33]. иметь мощность
иметь мощность  ?
? ?
? и
и  ; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа
; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа  бесконечное количество раз.
бесконечное количество раз. нормальным числом?
нормальным числом? ,Постоянная Эйлера — Маскерони, сама постоянная Хинчина и многие другие математические константы.
,Постоянная Эйлера — Маскерони, сама постоянная Хинчина и многие другие математические константы. и
и 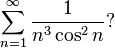
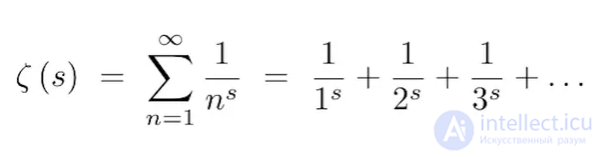
 Ни для одного из них не известно даже, является ли онорациональным числом, алгебраическим иррациональным или трансцендентным числом[44][45][46][47][48][49][50].
Ни для одного из них не известно даже, является ли онорациональным числом, алгебраическим иррациональным или трансцендентным числом[44][45][46][47][48][49][50]. и
и  алгебраически независимыми.
алгебраически независимыми. или
или 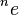 целыми числами при каком-либо положительном целом
целыми числами при каком-либо положительном целом  (см. тетрация). Неизвестно даже, является ли
(см. тетрация). Неизвестно даже, является ли  целым.
целым. быть целым, если
быть целым, если  — положительное целое число, а
— положительное целое число, а  — положительное рациональное, но не целое число (в частных случаях
— положительное рациональное, но не целое число (в частных случаях  ответ отрицателен).
ответ отрицателен). алгебраическим или трансцендентным числом (хотя известно, что он иррационален).
алгебраическим или трансцендентным числом (хотя известно, что он иррационален). рациональным, алгебраическим иррациональным или трансцендентным числом. Аналогичная проблема для тетрации любой большей высоты также открыта.
рациональным, алгебраическим иррациональным или трансцендентным числом. Аналогичная проблема для тетрации любой большей высоты также открыта.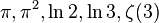 [52].
[52].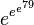 целым числом.
целым числом. для всех натуральных
для всех натуральных  ?
? для всех целых
для всех целых 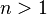 ?
? - фиксированное целое число
- фиксированное целое число 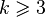 , то
, то 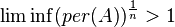 для
для  из
из  . Здесь
. Здесь 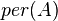 - перманент матрицы
- перманент матрицы  ,
,  - множество всех
- множество всех 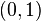 - матриц порядка
- матриц порядка  c
c  единицами в каждой строке и каждом столбце[54].
единицами в каждой строке и каждом столбце[54].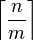 .[55]
.[55] .
.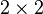 определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу.[60]
определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу.[60] , где
, где 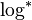 — итерированный логарифм (англ.).
— итерированный логарифм (англ.).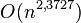 (однако с непрактично большим коэффициентом).
(однако с непрактично большим коэффициентом). состояниями и алфавитом
состояниями и алфавитом  на заполненной нулями ленте? Известно, что нет алгоритма (а значит, и рекурсивно аксиоматизируемой формальной теории), который может решить этот вопрос для всех
на заполненной нулями ленте? Известно, что нет алгоритма (а значит, и рекурсивно аксиоматизируемой формальной теории), который может решить этот вопрос для всех  , и пока известны только значения для
, и пока известны только значения для 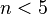 .[63]
.[63] функций одного натурального переменного
функций одного натурального переменного  , построенных из термов
, построенных из термов  и замкнутых относительно сложения,умножения и возведения в степень. Для функций
и замкнутых относительно сложения,умножения и возведения в степень. Для функций  из этого множества будем писать
из этого множества будем писать 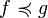 , если
, если 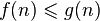 выполняется для всех достаточно больших
выполняется для всех достаточно больших  . Известно, что отношение
. Известно, что отношение  вполне упорядочивает множество
вполне упорядочивает множество  . Какой ординал соответствует этому упорядочению? (Известно, что он не меньше чем
. Какой ординал соответствует этому упорядочению? (Известно, что он не меньше чем  и не больше чем первый критический ординал
и не больше чем первый критический ординал  )[64][65] Аналогичные вопросы возникают при добавлении в множество разрешенных операторов дополненная тетрации,пентации и гипероператоров более высоких порядков (проблема Скулема, дополненная только тетрацией, была решена в 2010 году).[66][67]
)[64][65] Аналогичные вопросы возникают при добавлении в множество разрешенных операторов дополненная тетрации,пентации и гипероператоров более высоких порядков (проблема Скулема, дополненная только тетрацией, была решена в 2010 году).[66][67] , большие
, большие  [69].
[69].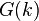 существует модель Цермело-Френкеля, в которой
существует модель Цермело-Френкеля, в которой 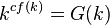 для всех кардиналов
для всех кардиналов  [70].
[70]. , что декартово произведение m-компактных пространств всегда m-компактно. Неизвестно также, совпадало бы наименьшее из этих чисел с наименьшим измеримым числом или нет.
, что декартово произведение m-компактных пространств всегда m-компактно. Неизвестно также, совпадало бы наименьшее из этих чисел с наименьшим измеримым числом или нет.
 -стадийного метода Рунге — Кутты (одностадийный = метод Эйлера =
-стадийного метода Рунге — Кутты (одностадийный = метод Эйлера =  , двухстадийный =модифицированный метод Эйлера =
, двухстадийный =модифицированный метод Эйлера =  , четырехстадийный = классический метод Рунге — Кутты =
, четырехстадийный = классический метод Рунге — Кутты = 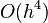 , пятистадийный = метод Фельберга (англ.) = тоже
, пятистадийный = метод Фельберга (англ.) = тоже 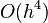 ).
).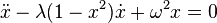
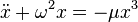
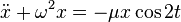
 лиц для
лиц для 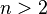 [87].
[87].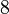 нерешенных проблем теории игр есть в книге [88].
нерешенных проблем теории игр есть в книге [88]. , входящее в дискретную часть разложения регулярного представления, реализуется в пространстве
, входящее в дискретную часть разложения регулярного представления, реализуется в пространстве  - когомологий подходящего пучка на пространстве
- когомологий подходящего пучка на пространстве  , где
, где  - компактная картановская подгруппа в
- компактная картановская подгруппа в  [90].
[90].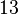 нерешенных проблем теоретико-множественной топологии есть в статье [92].
нерешенных проблем теоретико-множественной топологии есть в статье [92]. числа выбросов случайного процесса в общем случае не имеет законченного и компактного решения[95].
числа выбросов случайного процесса в общем случае не имеет законченного и компактного решения[95].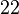 нерешенных задач теории операторов в банаховом пространстве есть в книге[97].
нерешенных задач теории операторов в банаховом пространстве есть в книге[97].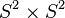 риманова метрика положительной кривизны?
риманова метрика положительной кривизны?
Комментарии
Оставить комментарий
введение в математику. основы
Термины: введение в математику. основы