Лекция
Сразу хочу сказать, что здесь никакой воды про операции в математике, и только нужная информация. Для того чтобы лучше понимать что такое операции в математике, сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, тетрация, пентация, радикал, звезда ходжа , настоятельно рекомендую прочитать все из категории введение в математику. основы.
Операция — отображение, ставящее в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Термин «операция» как правило применяется к арифметическим или логическим действиям, в отличие от термина «оператор», который чаще применяется к некоторым отображением множества на себя, имеющим замечательные свойства.

Операция  — отображение, областью определения которого является прямое произведение нескольких множеств. Математически операцию можно записать какотображение
— отображение, областью определения которого является прямое произведение нескольких множеств. Математически операцию можно записать какотображение  (
(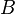 и
и 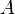 могут совпадать), где
могут совпадать), где  называется арностью операции.
называется арностью операции.
Арность
Операции различаются по количеству множеств, декартово произведение которых является ее областью определения. Например, операция может быть унарная, если она отображает один элемент множества на один элемент множества, или бинарная, если сопоставляет двум элементам множества один элемент.
Алгебраической операцией называется операция  , у которой
, у которой 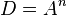 и
и 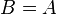 , где
, где  — арность, т.е.
— арность, т.е.  .
.
Операции могут обладать или не обладать различными свойствами. Например:
 », когда
», когда 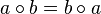 .
.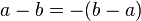 .
. », когда
», когда 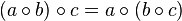 .
.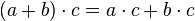 .
. » транзитивна, если из соотношений
» транзитивна, если из соотношений 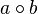 и
и 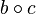 следует, что
следует, что  .
.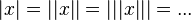 .
.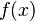 верно, что
верно, что 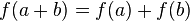 , то функция аддитивна.
, то функция аддитивна.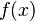 верно, что
верно, что 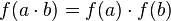 , то функция мультипликативна.
, то функция мультипликативна.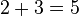 .
.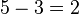 .
. .как крестик (×), точку (⋅) или звездочку (∗).
.как крестик (×), точку (⋅) или звездочку (∗).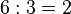 .Деление обозначается двоеточием
.Деление обозначается двоеточием 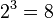 .
.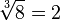 .
.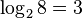 .
.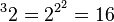 .
.Сложение и отрицание являются элементарными арифметическими операциями. Об этом говорит сайт https://intellect.icu . Все остальные, более сложные операции, получаются в результате гиперопераций. Так, сложение и вычитание относят к операциям первой ступени; умножение и деление — к операциям второй ступени; возведение в степень, извлечение корня и логарифмирование — к операциям третьей ступени; тетрация и ее обратные операции являются редко используемыми операциями четвертой ступени, однако такое гипероперирование можно продолжать бесконечно, вплоть до операций 5-й, 6-й и высших ступеней.
 .
.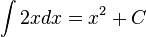 .
.Логические операции — операции над элементами из множества двух элементов: «истина» и «ложь», или «1» и «0».
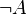 ) — унарная операция; преобразует «1» в «0», а «0» в «1».
) — унарная операция; преобразует «1» в «0», а «0» в «1». ) — бинарная операция; возвращает «1», только если оба аргумента «1».
) — бинарная операция; возвращает «1», только если оба аргумента «1». ) — бинарная операция; возвращает «0», только если оба аргумента «0».
) — бинарная операция; возвращает «0», только если оба аргумента «0».Мои читатели, знакомые с миром больших, нет нереально больших, чисел конечно знакомы с этой математической операцией, но остальные - навряд ли. Итак:
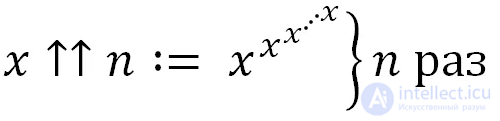
Операция придумана для записи чисел, когда привычное нам возведение в степень уже не может выразить их масштаба. Для понимания того, насколько огромные числа можно записать с помощью нотации Кнута, приведу пример:
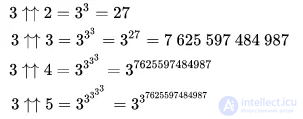
Числа возрастают не просто быстро, а невообразимо быстро!
Ах да! Стрелочек в нотации Кнута может быть и 3 и больше...намного больше.
Воскликните Вы: "Что же здесь нового?". Однако я больше чем уверен, что никому из Вас этот знак не встречался!

Да, все очень просто: одним знаком заменили знак равно и константу.
Аббревиатура из теории множеств (которую, кстати на своем канале пытаюсь рассказать доступно и с нуля). Пусть дано множество X, которое является подмножеством M, тогда
Cупремум - это наименьший элемент множества M, который больше любого элемента множества X. Пусть множество X= {1,2,3,4}, и оно входит в множество натуральных чисел N. Тогда супремумом множества X является 4 : действительно - это наименьшее из натуральных чисел, большее любого элемента из X. Обозначается sup(X).
Инфимум - это наибольший элемент множества M, который меньше любого элемента множества X. Пусть множество X= {3,4,5}, и оно входит в множество натуральных чисел R. Тогда инфимумом множества X является 3 : действительно - это наибольшее из натуральных чисел, меньшее любого элемента из X. Обозначается inf(X).
Естественно, что люди, знакомые с радиотехническими цепями очень часто используют эту аббревиатуру. Про остальных такого не скажу. Итак:

Сигнум - это кусочно-постоянная функция, принимающая всего лишь три значения. Например, sgn(5) = 1 , sgn (10!) = 1, sgn (-3,14) = -1 и только sgn(0)=0. Не кажется ли данная функция слишком простой и где она применяется, знаете?
Нет, это не знакомый всем со школьных времен корень. Это - нечто более интересное, но менее употребимое. По определению, радикалом числа является произведение его простых делителей. Обозначается rad(N).
Например, у числа 35 делители: 5 и 7, тогда rad(35) = 35. Возьмем число 504= 2^3 * 3^2 *7 - простые делители - это 2,3,7. Тогда rad(504) = 2*3*7=42.
Эта, казалось бы, простая математическая операция является одним из главных инструментов формулировки и доказательства ABC-гипотезы - чрезвычайно простой, но в тоже время пока недоказанной и важнейшей теоремой в области чисел, имеющей большое прикладное значение.
6. звезда ходжа — важный линейный оператор из пространства q-векторов в пространство (n − q)-форм. Метрический тензор задает канонический изоморфизм между пространствами q-форм и q-векторов, поэтому обычно звездой Ходжа называют оператор из пространства дифференциальных форм размерности q в пространство форм размерности n − q.
Этот оператор был введен Вильямом Ходжем.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про операции в математике Надеюсь, что теперь ты понял что такое операции в математике, сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, тетрация, пентация, радикал, звезда ходжа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы
Из статьи мы узнали кратко, но содержательно про операции в математике
Комментарии
Оставить комментарий
введение в математику. основы
Термины: введение в математику. основы