Гипероператор кратко

Привет, Вы узнаете о том , что такое гипероператор, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое гипероператор , настоятельно рекомендую прочитать все из категории Алгебра.

В математике гипероператор — это обобщение традиционных операторов (арифметических операций сложения, умножения и возведения в степень, рассматриваемых как гипероператоры 1-го, 2-го и 3-го порядка соответственно), на высшие порядки. В общем случае, из-за некоммутативности гипеоператор имеет две обратные функции — гиперкорень (например Суперкорень для 4-го порядка) и гиперлогарифм (Суперлогарифм).

Гипероператор — это общее понятие, которое охватывает ряд операций, являющихся обобщениями элементарных арифметических операций (сложение, умножение, возведение в степень и т.д.). Основная последовательность гипероператоров начинается со следующих операций:

1. h₁(a, b) = a + b (сложение),
2. h₂(a, b) = a × b (умножение),
3. h₃(a, b) = a^b (возведение в степень),
4. h₄(a, b) — это тетрация (повторное возведение в степень),
5. h₅(a, b) — пентация, и так далее.

Каждый следующий гипероператор можно рассматривать как повторение предыдущего. Например, пентация — это повторение тетрации, где в качестве показателя степени используется значение второго аргумента.

Эта последовательность позволяет определять более высокоуровневые операции, которые применяются в математике для работы с большими числами и исследований в области теории вычислений, рекурсивных функций и других дисциплин.

История

В 1928 году ученик Давида Гильберта, математик Вильгельм Аккерман опубликовал в качестве примера всюду определенной, не являющейся примитивно рекурсивной вычислимой функцию от трех аргументов , такую, что для она определяла операции сложения, умножения и возведения в степень соответственно:

;

;

.

С 1976 года, после публикации стрелочной нотации Кнута, оригинальную функцию Аккермана стало возможным записать в более удобном виде:

.

Помимо ее исторической роли как первой всюду определенной не примитивно рекурсивной вычислимой функции, оригинальная функция Аккермана расширяла основные арифметические операции за возведение в степень, хотя и не так хорошо, как специально предназначенные для этого функции вроде последовательности гипероператоров Гудстейна.

Определение

Гипероператор порядка с аргументами и (далее обозначаемый как ) рекурсивно определяется как результат многократного применения гипероператора порядка к последовательности из одинаковых аргументов, (начиная с умножения, каждый из которых равен ):

• сложение и — увеличение числа на количество единиц, равное

• умножение на — сложение числа с самим собой раз:
• возведение a в степень b — умножение числа на само себя раз
• 
• 

В последнем выражении операции выполняются справа налево, что является существенным, так как гипероператоры порядка {\displaystyle n>2} не являются ни коммутативными, ни ассоциативными. Об этом говорит сайт https://intellect.icu . Гипероператоры 4-го, 5-го и 6-го порядка называются «тетра́ция», «пента́ция» и «гекса́ция» соответственно.

В простейшем случае значения переменных , и {\displaystyle n} ограничиваются натуральными числами. Возможные обобщения гипероператоров на произвольные действительные или комплексные числа пока мало изучены.

Разные математики обозначают гипероператоры по-разному:

• Кнут использует стрелки ;
• Конвей использует стрелки .

В итоге получаем:

Обобщение первых трех операций (сложение, умножение, возведение в степень) в инфиксной форме имеет вид:

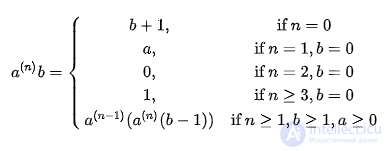
Тогда гипероператор определяется как

Распишем для первых натуральных четырех n:

Обратные операции

Как уже говорилось выше, в силу некоммутативности (в общем случае) гипероператор имеет две обратные функции — гиперкорень и гиперлогарифм.

В силу коммутативности, гиперкорень и гиперлогарифм сложения совпадают и образуют вместе обратную операцию сложения — вычитание.

Точно так же совпадают обратные операции умножения, образуя одну обратную операцию умножения — деление.

Уже для возведения в степень обратные функции становятся различными (корень и логарифм).

Обратные операции обобщаются для гипероператора любого порядка.

Альтернативные операции

Вычисление слева направо

Альтернативная операция может быть получена путем вычисления слева направо и в силу коммутативности и ассоциативности операций сложения и умножения эта операция совпадает с Гипероператором при :

• 
• 
• 

Для гипероператора вычисление слева направо (то есть альтернативная операция) отличается от гипероператора и проводит к другому результату, например, для получим гипероператор тетрацию: .

Но вычисление степенной башни слева направо приведет к неверному итогу: .

Применение

Практическое применение гипероператоров ограничено специфическими областями, поскольку операции уровня выше возведения в степень (например, тетрация, пентация) быстро дают очень большие числа, которые сложно обрабатывать. Однако в некоторых научных и инженерных сферах гипероператоры могут быть полезны:

1. Теория вычислений и сложность алгоритмов

Гипероператоры могут использоваться для анализа алгоритмов с очень высокой степенью вычислительной сложности. Например, некоторые задачи в области теоретической информатики, такие как вычисление больших чисел или построение вычислительных схем, требуют операций, которые можно описать с помощью гипероператоров.

2. Криптография

В криптографии используются большие числа для создания сложных ключей и шифров. Возведение в степень и другие гипероператоры могут играть роль в создании более сложных шифровальных схем и методов защиты данных.

3. Астрономия и физика

В моделях, где необходимо работать с очень большими числами (например, оценки размера вселенной или продолжительности времени существования объектов), гипероператоры могут быть полезны для удобного представления таких чисел.

4. Теоретическая математика

В математике гипероператоры используются в исследованиях больших чисел, таких как число Грэма, которое связано с проблемой Рамсея. Это число слишком велико для записи с помощью обычных степеней, и гипероператоры позволяют его описать.

5. Числовые теории и комбинаторика

В области числовых теорий, особенно когда речь идет о быстром росте последовательностей, гипероператоры могут использоваться для описания таких функций и их свойств.

Несмотря на ограниченное прямое применение в повседневных вычислениях, гипероператоры играют важную роль в теоретических исследованиях и решении задач, связанных с экстремально большими числами.

Вау!! 😲 Ты еще не читал? Это зря!

• гексация ,
• тетрация , пентация ,
• Функция Аккермана
• Функция Веблена
• Пси- функции Бухгольца
• Быстрорастущая иерархия
• Медленнорастущая иерархия
• Иерархия Харди

• Возведение в степень
• Суперкорень
• Суперлогарифм

Исследование, описанное в статье про гипероператор, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое гипероператор и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра

Из статьи мы узнали кратко, но содержательно про гипероператор