Лекция
Привет, Вы узнаете о том , что такое простое число, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое простое число, простые числа , настоятельно рекомендую прочитать все из категории Алгебра.
простое число — натуральное (целое положительное) число, имеющее ровно два различных натуральных делителя — единицу и самого себя . Другими словами, число является простым, если оно больше
и при этом делится без остатка только на
и на
. К примеру,
— простое число, а
не является простым числом, так как, помимо
и
, оно также делится на
и на
.
Основная теорема арифметики устанавливает центральную роль простых чисел в теории чисел: любое целое число, большее , либо является простым, либо может быть выражено как произведение простых чисел, причем это выражение единственно с точностью до порядка сомножителей. Именно чтобы обеспечить единственность в этой теореме, единица не считается простым числом (иначе можно включать произвольно много единиц в любое разложение , например,
и так далее).
Натуральные числа, которые больше единицы и не являются простыми, называются составными. Таким образом, все натуральные числа разбиваются на три класса: единицу (имеющую один натуральный делитель), простые числа (имеющие два натуральных делителя) и составные числа (имеющие больше двух натуральных делителей) . Изучением свойств простых чисел занимается теория чисел. Как простых, так и составных чисел бесконечно много.
Последовательность простых чисел начинается так:
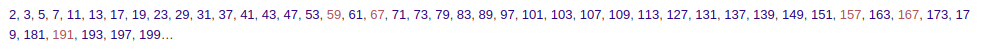
Свойство числа быть простым называется простотой. Простой, но медленный метод проверки простоты заданного числа n известен как перебор делителей; более эффективные алгоритмы описаны ниже.
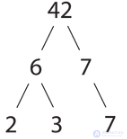
Разложение числа 42 на простые множители:
Многие проблемы, касающиеся простых чисел, остаются открытыми, смотри ниже.
Простые числа широко используются в математике и в смежных науках — например, во многих алгоритмах информационных технологий, таких как криптосистема с открытым ключом, которая использует такие свойства, как сложность разложения чисел на простые множители .
Существуют обобщения понятия простого числа для произвольных колец и других алгебраических структур, смотри ниже.

Неизвестно, когда было определено понятие простого числа, однако первые свидетельства понимания таких чисел относятся к верхнему палеолиту, что подтверждается костью Ишанго .
В сохранившихся записях древних египтян есть намеки на то, что у них были некоторые сведения о простых числах: например, папирус Райнда относящийся ко II тысячелетию до н. э. содержит в себе таблицу, выражающую дроби вида 2/n через сумму двух, трех или четырех дробей с числителями, равными единице, и различными знаменателями. Разложения дробей, знаменатели которых имеют общий делитель, похожи, что свидетельствует о том, что египтяне по крайней мере знали разницу между простым числом и составным .
Однако самые ранние сохранившиеся исследования простых чисел исходят от древних греков. Начала Евклида (около 300 г. до н. э.) содержат важные теоремы о простых числах, включая бесконечность простых чисел, лемму Евклида и основную теорему арифметики . В древней Греции также было придумано решето Эратосфена, простой алгоритм нахождения всех простых чисел от 1 до n.
После греков мало что произошло в изучении простых чисел до XVII века . В 1640 году Пьер де Ферма сформулировал (без доказательства) малую теорему Ферма (позже доказанную Лейбницем и Эйлером) и теорему о сумме двух квадратов. Ферма также высказал предположение, что все числа вида + 1 — простые (они были названы числами Ферма) и доказал это до n = 4 (или
+ 1). Однако Эйлер показал, что уже следующее число Ферма при n = 5 (или
+ 1) является составным (делится на число 641). На сегодняшний день нет других известных чисел Ферма, являющихся простыми. В то же время французский монах Марен Мерсенн обратил внимание на простые числа вида 2p — 1, где p — простое (не все числа такого вида являются простыми) . Их назвали простыми числами Мерсенна в его честь.
Работа Эйлера в теории чисел включала в себя множество сведений о простых числах. Он показал что бесконечный ряд 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + … является расходящимся. Также в 1747 году он показал, что четные совершенные числа — это целые числа вида , где второй множитель является простым Мерсенна. В переписке Эйлера с Христианом Гольдбахом последний сформулировал знаменитую гипотезу Гольдбаха о представлении любого четного числа, начиная с 4, в виде суммы двух простых, которая до сих пор не доказана[10].
С начала XIX века внимание многих математиков обратилось к изучению асимптотического распределения простых чисел[10]. Лежандр и Гаусс независимо друг от друга высказали предположение, что плотность простых чисел в среднем близка к величине, обратно пропорциональной натуральному логарифму[11].
Долгое время считалось, что простые числа имеют ограниченное применение за пределами чистой математики. Ситуация изменилась в 1970-е годы, когда появились концепции криптографии с открытым ключом, в них простые числа составляли основу первых алгоритмов, таких как алгоритм шифрования RSA[12].
Представление натурального числа в виде произведения простых называется разложением на простые или факторизацией числа. На настоящий момент неизвестны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует. На предполагаемой большой вычислительной сложности задачи факторизации базируется криптосистема RSA и некоторые другие. Факторизация с полиномиальной сложностью теоретически возможна на квантовом компьютере с помощью алгоритма Шора[13].
Основная теорема арифметики утверждает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причем единственным способом с точностью до порядка следования сомножителей[14]. Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел. Например:
Как было показано в этом примере, один и тот же простой делитель может появляться несколько раз. Разложение:
n = p1 · p2 · ... · pt
числа n на (конечное число) простых множителей p1, p2, … ,pt называется разложением на простые множители числа n. Основная теорема арифметики может быть перефразирована таким образом: любое разложение на простые числа будет тождественным с точностью до порядка делителей. На практике для большинства чисел есть много простых алгоритмов разложения на множители, все они дают один и тот же результат[13].
Большинство древних греков даже не считали числом, поэтому они не могли считать его простым[15]. К Средним векам и эпохе Возрождения многие математики включали
в качестве первого простого числа[16]. В середине XVIII века Христиан Гольдбах внес в список
в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером; однако сам Эйлер не считал
простым числом[17]. В XIX веке многие математики по-прежнему считали число
простым числом. Например, список простых цифр Деррика Нормана Лемера до
числа, переизданный 1956 году, начинался с
в качестве первого простого числа. Говорят, что Анри Лебег является последним математиком, который назвал
простым[18]. К началу XX века математики стали приходить к консенсусу о том, что
не является простым числом, а скорее формирует свою специальную категорию — «единицу»[16].
Если считать простым числом, то основная теорема Евклида об арифметике (упомянутая выше) не будет выполняться, как указано. Например, число
может быть разложено как 3 · 5 и 1 · 3 · 5. Если бы
являлась простым числом, эти два варианта считались бы разными факторизациями
, следовательно утверждение этой теоремы пришлось бы изменить[16]. Точно так же решето Эратосфена работало бы неправильно, если бы
считалась простым: модифицированная версия решета, которая предполагает, что
является простым числом, исключает все множители кратные
(то есть все остальные числа) и дает на выходе только одно число —
. Кроме того, простые числа имеют несколько свойств, которых нет у числа
, таких как отношение числа к его соответствующему значению функции тождества Эйлера или суммы функции делителей .
Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают решето Эратосфена, решето Сундарама и решето Аткина[19].
Однако, на практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым. Алгоритмы, решающие эту задачу, называются тестами простоты. Существует множество полиномиальных тестов простоты, но большинство их являются вероятностными (например, тест Миллера — Рабина) и используются для нужд криптографии[20]. В 2002 году было доказано, что задача проверки на простоту в общем виде полиномиально разрешима, но предложенный детерминированный тест Агравала — Каяла — Саксены имеет довольно большую вычислительную сложность, что затрудняет его практическое применение[21].
Для некоторых классов чисел существуют специализированные эффективные тесты простоты (см. ниже).
Тестом простоты (или проверкой простоты) называется алгоритм, который, приняв на входе число, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Задача теста простоты относится к классу сложности P, то есть время работы алгоритмов ее решения зависит от размера входных данных полиномиально, что было доказано в 2002 году[22]. Появление полиномиального алгоритма предсказывалось существованием полиномиальных сертификатов простоты и, как следствие, тем, что задача проверки числа на простоту принадлежала классам NP и co-NP одновременно.
Существующие алгоритмы проверки числа на простоту могут быть разделены на две категории: истинные тесты простоты и вероятностные тесты простоты. Результатом вычислений истинных тестов всегда является факт простоты либо составности числа. Вероятностный тест показывает, является ли число простым с некоторой вероятностью. Числа, удовлетворяющие вероятностному тесту простоты, но являющиеся составными, называются псевдопростыми[23]. Одним из примеров таких чисел являются числа Кармайкла[24].
Одним из примеров истинных тестов простоты является тест Люка-Лемера для чисел Мерсенна. Очевидный недостаток этого теста заключается в его применимости только к числам определенного вида. Среди других примеров можно привести основанные на малой теореме Ферма[25]
А также:
К вероятностным тестам простоты относят:
Уже в течение многих столетий поиск «больших» простых чисел вызывает интерес математиков. В последние десятилетия эти исследования приобрели прикладное значение из-за применения таких чисел в ряде алгоритмов шифрования, таких как RSA[12].
В семнадцатом столетии Марен Мерсенн предположил, что числа вида простые (при n ≤ 257) только для n равных 2, 3, 5, 7, 13, 19, 31, 67, 127 и 257.[11] Проверка верности предположения была намного выше возможностей того времени. Только в XX веке было обнаружено, что гипотеза была ложной и, вероятно, сделана «слепо», поскольку Мерсенн не учел три случая (для n = 61, 89 и 107); кроме того, оказалось, что числа, соответствующие n = 67 и n = 257 — составные[11].
В 1876 году Эдуард Люка доказал, что число M 127 (39-значное число) — простое, оно оставалось самым большим известным простым числом до 1951 года, когда были найдены (44 цифры) и, немного позднее,
(из 79 цифр) — последнее простое число, которое было найдено с помощью электронного калькулятора. С тех пор все последующие большие простые числа были обнаружены с помощью компьютера: с 1952 года (когда SWAC показал, что M 521 является простым), по 1996 год они были найдены суперкомпьютером, и все были простыми Мерсенна (найденные с использованием теста Люка-Лемера, специфического алгоритма для таких чисел), за исключением числа
, которое было рекордом между 1989 и 1992 годами[27].
Некоторые задачи математики с использованием факторизации требуют ряд очень больших простых чисел, выбранных случайным образом. Об этом говорит сайт https://intellect.icu . Алгоритм их получения, основанный на постулате Бертрана (Для любого натурального n ≥ 2 найдется простое число p в интервале n < p < 2n.)[28]:

Время решения задачи этим алгоритмом не определено, но есть большая вероятность, что оно всегда является полиномиальным, пока имеется достаточно простых чисел, и они распределены более-менее равномерно. Для простых случайных чисел эти условия выполняются[21].
Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма[26].
Пусть N, S — нечетные натуральные числа, N-1 = S*R, причем для каждого простого делителя q числа S существует целое число такое, что
,
Тогда каждый простой делитель p числа N удовлетворяет сравнению
Следствие. Если выполнены условия теоремы Ферма и , то N — простое число.[26]
Покажем теперь, как с помощью последнего утверждения, имея большое простое число , можно построить существенно большее простое число
. Выберем для этого случайным образом четное число
на промежутке
и положим
. Затем проверим число
на отсутствие малых простых делителей, разделив его на малые простые числа; испытаем
некоторое количество раз с помощью алгоритма Рабина. Если при этом выяснится, что
— составное число, следует выбрать новое значение
и опять повторить вычисления. Так следует делать до тех пор, пока не будет найдено число N, выдержавшее испытание алгоритмом Рабина достаточно много раз. В этом случае появляется надежда на то, что
— простое число, и следует попытаться доказать простоту с помощью тестов простоты[26].
Простых чисел бесконечно много. Это утверждение упоминается как теорема Евклида в честь древнегреческого математика Евклида, поскольку первое известное доказательство этого утверждения приписывается ему. Известно еще много доказательств бесконечности простых чисел, в том числе аналитическое доказательство Эйлера, доказательство Гольдбаха на основе чисел Ферма[29], доказательство Фурстенберга с использованием общей топологии и элегантное доказательство Куммера.
Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа[30]. Один из рекордов поставил в свое время Эйлер, найдя простое число 231 − 1 = 2 147 483 647.
Наибольшим известным простым числом по состоянию на январь 2019 года является число Мерсенна M82 589 933 = 282 589 933 − 1. Оно содержит 24 862 048 десятичных цифр; в книге с записью этого числа было бы около девяти тысяч страниц. Его нашли 7 декабря 2018 года в рамках проекта по распределенному поиску простых чисел Мерсенна GIMPS. Предыдущее самое большое известное простое число, открытое в декабре 2017 года, было на 1 612 623 знаков меньше[31].
Числа Мерсенна выгодно отличаются от остальных наличием эффективного теста простоты: теста Люка — Лемера. Благодаря ему простые числа Мерсенна давно удерживают рекорд как самые большие известные простые.
За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила[32] денежные призы соответственно в 150 000 и 250 000 долларов США[33]. Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр.
Существует ряд чисел, простота которых может быть установлена эффективно с использованием специализированных алгоритмов.
Для поиска простых чисел обозначенных типов в настоящее время используются проекты распределенных вычислений GIMPS, PrimeGrid, Ramsey@Home, Seventeen or Bust, Riesel Sieve, Wieferich@Home.
Простые числа являются фундаментальными компонентами во многих областях математики.
Арифметические функции, а именно функции, определенные на множестве натуральных чисел и принимающих значения во множестве комплексных чисел, играют решающую роль в теории чисел. В частности, среди них наиболее важными являются мультипликативные функции, то есть функции , обладающие следующим свойством: если пара
состоит из взаимно простых чисел, то имеет место равенство[59]
Примерами мультипликативных функций являются функция Эйлера , которая ставит в соответствие числу
количество натуральных чисел, меньших n и взаимно простых с ним и количество делителей числа n[60]. Значение этих функций от степени простого числа:
Арифметические функции можно легко вычислить, зная значения, которые они принимают для степеней простых чисел[59]. На самом деле из разложения натурального числа n на множители
мы имеем, что
и следовательно, возвращаясь к задаче вычисления получается что вычислить
от каждой степени простого делителя обычно проще, чем вычислить
по общей формуле.[61]
Например, чтобы узнать значение функции Эйлера от n = 450 = 2 × 3 2 × 5 2, достаточно вычислить
В модульной арифметике простые числа играют очень важную роль: кольцо вычетов является полем тогда и только тогда, когда n является простым.[48] Также существование первообразного корня кольца
привязано к простым числам: оно существует, только если n — простое число, 1, 2, 4 или число в форме
, где p нечетно.
Одной из важнейших теорем модульной арифметики является малая теорема Ферма[52]. Эта теорема утверждает, что для любого простого числа р и любого натурального числа a имеем:
или для любого простого р и любого натурального а не делящегося на р, справедливо:
Это свойство можно использовать для проверки того, что число не является простым. На самом деле, если n таково, что:
для некоторого натурального а, то n не может быть простым[52]. Однако это свойство не может быть использовано для проверки числа на простоту: есть некоторые числа, называемые числами Кармайкла (наименьшее — 561) для которых это будет неверно. Числом Кармайкла называется составное число, которое является псевдопростым числом по каждому основанию b, взаимно простому с n. В 1994 году Уильям Роберт Альфорд, Эндрю Гранвиль и Карл Померанс показали, что таких чисел бесконечно много[62].
Простые числа также играют основополагающую роль в алгебре. В теории групп, группа, в которой каждый элемент является степенью простого числа р называется р-группой[63]. P-группа является конечной, тогда и только тогда, когда порядок группы (число ее элементов) является степенью р. Примером бесконечной р-группы является p-группа Прюфера[64]. Известно, что p-группы имеют нетривиальный центр и, следовательно, не могут быть простыми (кроме группы с p элементами); если группа конечна, более того, все нормальные подгруппы пересекают центр нетривиальным образом.
Примером таких групп является циклическая группа умножения по модулю простого числа[65].
Все группы порядка p являются циклическими и поэтому абелевыми; также абелева каждая группа порядка p 2. Кроме того, любая конечная абелева группа изоморфна прямому произведению конечного числа циклических р-групп.
В теореме Коши утверждается, что если порядок конечной группы G делится на простое число p, то G содержит элементы порядка p. Эта теорема обобщается теоремами Силова[50].
Некоторые алгоритмы криптографии с открытым ключом, такие как RSA и обмен ключами Диффи-Хеллмана, основаны на больших простых числах (обычно 1024—2048 бит). RSA полагается на предположение, что намного проще (то есть более эффективно) выполнять умножение двух (больших) чисел x и y, чем вычислять взаимно простые x и y, если известно только их произведение . Обмен ключами Диффи-Хеллмана основан на том, что существуют эффективные алгоритмы возведения в степень по модулю, а обратная операция — дискретного логарифмирования считается сложной[66][67].
Трудность факторизации больших чисел привела к разработке первого эффективного метода криптографии с открытым ключом — RSA.[68] В этой криптографической системе, человек, который должен получить зашифрованное сообщение, генерирует ключ: выбираются два различных случайных простых числа и
заданного размера (обычно используются, 1024- или 2048-битные числа). Далее вычисляется их произведение
, называемое модулем. Вычисляется значение функции Эйлера от числа
:
. Выбирается целое число
(
), взаимно простое со значением функции
. Обычно в качестве
берут небольшие простые числа (например, простые числа Ферма). Число
называется открытой экспонентой (англ. public exponent). Вычисляется число
, называемое секретной экспонентой, мультипликативно обратное к числу e по модулю
. Пара
публикуется в качестве открытого ключа RSA (англ. RSA public key). Пара
играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете[12].
Теоретически можно получить закрытый ключ из общедоступной информации: в настоящее время для этого требуется факторизация числа , что делает передачу защищенного сообщения безопасной, если простые числа удовлетворяют определенным условиям и являются «достаточно большими». Пока не известно, существуют ли эффективные методы для расшифровки сообщения, не связанные с прямой атакой на факторизацию
, но было показано, что плохой выбор открытого ключа может сделать систему более уязвимой для таких атак.[69]
В 1991 году RSA Security опубликовала список полупростых чисел, предлагая денежные призы за разложение некоторых из них на множители, с целью подтверждения безопасности метода и поощрения исследования в этой области: инициатива называлась Challenge RSA Factoring.[70] На протяжении многих лет некоторые из этих чисел были разложены, а для других проблема факторизации все еще остается открытой; однако конкурс был завершен в 2007 году[70].
В разное время предпринимались попытки указать выражение, значениями которого при разных значениях входящих в него переменных были бы простые числа[54]. Л. Эйлер указал многочлен принимающий простые значения при n = 0, 1, 2, …, 40. Однако при n = 41 значение многочлена является составным числом. Можно доказать, что не существует многочлена от одной переменной n, который принимает простые значения при всех целых n[54]. П. Ферма предположил, что все числа вида 22k + 1 простые; однако Эйлер опроверг эту гипотезу, доказав, что число 225 + 1 = 4 294 967 297 — составное[54].
Тем не менее, существуют многочлены, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. Одним из примеров является многочлен
содержащий 26 переменных и имеющий степень 25. Наименьшая степень для известных многочленов такого типа — 5 при 42 переменных; наименьшее число переменных — 10 при степени около 1,6·1045[71][72]. Этот результат является частным случаем доказанной Юрием Матиясевичем диофантовости любого перечислимого множества.
Интересно, что приведенный выше многочлен, который порождает простые числа, сам разлагается на множители. Заметим, что второй множитель этого многочлена (в фигурных скобках) имеет форму: единица минус сумма квадратов. Таким образом, многочлен может принимать положительные значения (при положительных ) только если, каждый из этих квадратов (то есть каждый многочлен в квадратных скобках) равен нулю. В этом случае выражение в фигурных скобках будет равно 1[73].
До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау на Пятом Международном математическом конгрессе[74]:
Открытой проблемой является также существование бесконечного количества простых чисел во многих целочисленных последовательностях, включая числа Мерсенна[54], числа Фибоначчи, числа Ферма и др.
В начале статьи было дано определение простого числа: натуральное число называется простым, если у него ровно два делителя — единица и само число. Аналогичное понятие можно ввести и в других алгебраических структурах; чаще всего рассматривается коммутативные кольца без делителей нуля (области целостности)[78][79]. У таких колец, однако, могут быть делители единицы, образующие мультипликативную группу. Например, в кольце целых чисел существуют два делителя единицы: и
Поэтому все целые числа, кроме делителей единицы, имеют не два, а по меньшей мере четыре делителя; например, у числа 7 делителями являются
Это означает, что обобщение понятия простого числа должно опираться на иные его свойства.
Аналогом простого числа для области целостности является неприводимый элемент. который определяется следующим образом[80].
|
Ненулевой элемент |
Для целых чисел это определение означает, что неприводимыми элементами являются простые натуральные числа, а также противоположные им.
Из определения следует, что множество делителей неприводимого элемента состоит из двух частей: все делители единицы и произведения
на все делители единицы (эти произведения называются ассоциированными с
злементами). То есть количество делителей неприводимого
если оно конечно, вдвое больше количества делителей единицы в кольце.
Важное значение имеет аналог основной теоремы арифметики, который в обобщенном виде формулируется следующим образом[81]:
|
Кольцо называется факториальным, если в нем каждый ненулевой элемент, не являющийся делителем единицы, может быть представлен в виде произведения неприводимых элементов, причем это представление единственно с точностью до перестановки сомножителей и их ассоциированности (умножения на делители единицы). |
Не всякая область целостности факториальна, см. контрпример. Евклидово кольцо всегда факториально[82].
Существует другое, более узкое обобщение понятия простого числа, называемое простым элементом[80].
|
Ненулевой элемент |
Простой элемент всегда неприводим. В самом деле, если элемент простой и
то по определению простого элемента один из сомножителей, пусть это будет
делится на
то есть
Тогда
или, сокращая на
(в области целостности сокращение ненулевого множителя всегда возможно):
то есть
является делителем единицы. ■
Обратное, вообще говоря, неверно, неприводимый элемент может не быть простым, если кольцо не является факториальным. Пример[83]: рассмотрим кольцо чисел вида где
— целые числа. Число 3 в нем неприводимо, так как у него только 4 делителя:
. Однако оно не является простым элементом, в чем убеждает равенство:
Число 3 делит правую часть равенства, но не делит ни одного из сомножителей. Можно из этого факта сделать вывод, что рассмотренное кольцо не факториально; и в самом деле, равенство показывает, что разложение на неприводимые множители в этом кольце не однозначно.
Кольцо целых чисел факториально. В нем, как уже упоминалось выше, два делителя единицы.
Кольцо гауссовых чисел состоит из комплексных чисел вида где
— целые числа. Делителей единицы четыре:
Это кольцо факториально, неприводимыми элементами являются часть обычных простых чисел и «простые гауссовы» (например,
). См. критерий простоты гауссова числа.
Пример разложения для числа 2, которое в кольце гауссовых чисел не является простым: — неединственность разложения здесь кажущаяся, поскольку
ассоциирована с
, согласно равенству:
Кольцо целых чисел Эйзенштейна состоит из комплексных чисел следующего вида[84]:
где
— целые числа,
(кубический корень из единицы),
В этом кольце шесть делителей единицы: (±1, ±ω, ±ω2), оно евклидово и поэтому факториально. Неприводимые элементы (они же простые элементы) кольца называются простыми числами Эйзенштейна.
Критерий простоты: целое число Эйзенштейна является простым числом Эйзенштейна тогда и только тогда, когда выполняется одно из следующих взаимоисключающих условий:
Отсюда следует, что норма любого целого числа Эйзенштейна является либо простым натуральным числом, либо квадратом простого натурального числа[84].
Числа, ассоциированные или комплексно-сопряженные с простыми числами Эйзенштейна, также являются простыми числами Эйзенштейна.
Большое значение в алгебре имеет кольцо многочленов , образованное многочленами с коэффициентами из некоторого кольца
Делителями единицы являются здесь ненулевые константы (как многочлены нулевой степени). Кольцо многочленов евклидово и поэтому факториально. Если в качестве
взять поле вещественных чисел, то неприводимыми будут все многочлены 1-й степени и те многочлены 2-й степени, у которых нет вещественных корней (то есть их дискриминант отрицателен)[85].
Исследование, описанное в статье про простое число, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое простое число, простые числа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгебра
Термины: Алгебра