Бикватернион

Сразу хочу сказать, что здесь никакой воды про бикватернион, и только нужная информация. Для того чтобы лучше понимать что такое бикватернион , настоятельно рекомендую прочитать все из категории Алгебра.

бикватернион ы — комплексификация (расширение) обычных (вещественных) кватернионов.

Определение

Бикватернионы можно описать как множества чисел вида «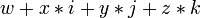»,   где w, x, y, z — есть те или иные «специальные  комплексные числа ». Альтернативный способ введения — Процедура Кэли — Диксона: это  гиперкомплексные числа  вида «»,  где a, b — любые кватернионы, а I — « мнимая единица  расширения». Об этом говорит сайт https://intellect.icu . Известны три разных вида бикватернионов, в зависимости от того, какого типа «комплексные» числа положены в основу этого представления (иначе говоря, каковы свойства расширяемой операции умножения для числа «I»):

• эллиптические (ординарные) (если  );
• параболические (дуальные) (если );
• гиперболические (двойные) (если )

История и применения

Об ординарных бикватернионах написал Гамильтон в 1844г. (см. Труды Ирландской Королевской Академии 1844 и 1850 стр.388). В число наиболее видных сторонников этих бикватернионов следует включить Александра Макфарлейна (en:Alexander Macfarlane), Артура У. Конвея, Людвика Зильберштейна (en:Ludwik Silberstein) иКорнелиуса Ланцоша. Единичная квази- сфера бикватернионов обеспечивает представление группы Лоренца, на которой основана  специальная теория относительности .

Двойные кватернионы изучал Клиффорд, Уильям. Дуальные кватернионы инструментально обеспечивают нестандартный анализ  обычных кватернионов. Далее, если не оговорено, речь идет об ординарных бикватернионах.

Свойства

«Алгебра бикватернионов» есть тензорное произведение алгебр C⊗H (взятое над вещественными числами), где C --- та или иная алгебра комплексных чисел, а H --- алгебра обычных (вещественных) кватернионов. Как C-алгебра бикватернионы изоморфны алгебре комплексных матриц 2x2 M₂(C).

...

Матричное представление

Есть три комплексные матрицы, для которых: 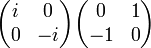 =  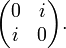 Притом квадрат каждой из этих матриц есть «минус единичная матрица », а если произведению этих матриц сопоставить произведение чисел i*j = k; j*i = -k. Получаем, что порождаемая этим матрицами подгруппа матричной группы изоморфна группе кватернионов. Следовательно, если сопоставить матрице  бикватернион q == u*1 + v*i + w*j + x*k, то для данной 2×2 комплексной матрицы, всегда существуют комплексные величины u, v, w, x в этой форме. Иначе говоря, кольцо комплексных матриц изоморфно^[1] кольцу (ординарных) бикватернионов.

Подалгебры

При рассмотрении (ординарных) бикватернионов как алгебры над полем вещественных чисел R, набор {1, I, i, Ii, j, Ij, k, Ik} образует базис, эта алгебра имеет вещественную размерность пространства восемь. Притом квадраты всех элементов Ii, Ij, Ik =«+1». Значит, вещественная подалгебра, образуемая  изоморфна кольцу, которое образуют двойные числа (с алгебраической структурой аналогичной строящейся над единичной гиперболой). Элементы Ij, Ik определяют такие же подалгебры.

Элементы  образуют подалгебру изоморфную бикомплексным числам (tessarine).

Третий вид подалгебры, т.н. «кокватернионы», порождается Ij, Ik, т.к. вещественное линейное подпространство с базисом {1, i, Ij, Ik} замкнуто по умножению (ведь Ij*Ik=-i). Указанный базис образует диэдрическую группу квадрата, а кокватернионы изоморфны алгебре вещественных матриц 2х2.

Квантовая механика и спинорная  алгебра , трактуют бикватернионы Ii, Ij, Ik (или их отрицание), рассматривая их в преставлении M(2,C), как матрицы Паули.

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про бикватернион Надеюсь, что теперь ты понял что такое бикватернион и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра