логарифмические уравнения кратко

Привет, Вы узнаете о том , что такое логарифмические уравнения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое логарифмические уравнения , настоятельно рекомендую прочитать все из категории Алгебра.

логарифмические уравнения - это уравнения, в которых логарифмические функции (например, натуральный логарифм или логарифм по другому основанию) играют важную роль.

Например: log₂(3x − 2) = 7.

Решение логарифмических уравнений основывается на определении логарифма, свойствах логарифмической функции и свойствах логарифма.

Они могут выглядеть следующим образом:

1. Простое логарифмическое уравнение:

   Это уравнение имеет вид log(base_a)(x) = b, где "log" - это логарифм, "a" - основание логарифма, "x" - переменная, и "b" - константа.

   Пример: log(x) = 3. В этом случае мы ищем значение "x", которое удовлетворяет уравнению logарифмическое уравнение с основанием 10.

2. Логарифмическое уравнение с переменными внутри логарифма:

   Это уравнение имеет вид log(base_a)(f(x)) = b, где "log" - логарифм, "a" - основание логарифма, "f(x)" - функция от переменной "x", и "b" - константа.

   Пример: log(2x + 1) = 4. Здесь мы ищем значение "x", которое удовлетворяет логарифмическому уравнению, где переменная "x" находится внутри логарифма с основанием 10.

Для решения логарифмических уравнений используются различные методы, включая:

1. Изоляция логарифма: Перемещение логарифма на одну сторону уравнения и применение обратной функции (возведение в степень) для выражения переменной.

2. Использование свойств логарифмов: Использование свойств логарифмов, таких как свойство перемножения и свойство деления, для упрощения уравнения.

3. Замена переменной: Иногда замена переменной может сделать уравнение более простым для решения.

4. Графический метод: Построение графиков функций и логарифмов может помочь в определении точек их пересечения.

5. Логарифмические и экспоненциальные тождества: Использование логарифмических и экспоненциальных тождеств, таких как тождество a^log(base_a)(x) = x, для упрощения уравнения.

Решение логарифмических уравнений может потребовать некоторых математических навыков и творческого подхода в зависимости от их сложности и формы.

Применение - логарифмических уравнений

Логарифмические уравнения находят применение в различных областях науки, инженерии, экономике и других дисциплинах. Вот некоторые примеры, где логарифмические уравнения могут быть полезными:

1. Экономика и финансы: Логарифмические уравнения могут использоваться для моделирования экономических процессов, таких как рост инвестиций или расчет будущей стоимости инвестиций на основе процентной ставки.

2. Биология: В биологии логарифмические уравнения могут применяться для моделирования роста населения организмов, распределения видов в экосистемах и других биологических явлений.

3. Инженерия: Логарифмические уравнения используются в различных инженерных расчетах, таких как определение звукоизоляции, анализ электрических цепей с логарифмической шкалой частот и расчет утечек в трубопроводах.

4. Медицина: В медицине логарифмические уравнения могут использоваться для анализа роста популяции бактерий, расчета времени полувыведения лекарств из организма и других медицинских приложений.

5. Геология: В геологии логарифмические уравнения могут применяться для оценки времени, прошедшего с момента формирования горных пород, или для анализа распределения элементов в геологических образцах.

6. Компьютерные науки: Логарифмические уравнения могут возникать при анализе алгоритмов и сложности вычислений, особенно в контексте алгоритмов сортировки и поиска.

7. Физика: В физике логарифмические уравнения используются для описания процессов деградации радиоактивных веществ, изменения давления в атмосфере с высотой и других явлений.

8. Экология: Логарифмические уравнения могут быть полезными при анализе динамики популяций животных и растений, оценке экологических балансов и других экологических исследованиях.

Эти примеры показывают, что логарифмические уравнения имеют широкий спектр приложений и могут быть мощным инструментом для анализа и моделирования различных процессов и явлений в разных областях знаний.

Примеры решения логарифмических уравнений

1.Решите уравнение:

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Мы «убираем логарифмы» не просто так, а пользуясь свойством монотонности логарифмической функции.

Получаем:

Решая логарифмические уравнения, не слудует учитывать область допустимых значений логарифма. Помним, что выражение определено при .

Найдя корень уравнения, подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи.

2. Решите уравнение: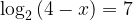

В левой части уравнения – логарифм, в правой – число 7. Об этом говорит сайт https://intellect.icu . Используя основное логарифмическое тождество, представим число 7 в виде .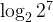

Ответ: -124

3. Решите уравнение: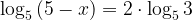

Обратите внимание на 2 перед логарифмом в правой части уравнения. Сейчас оно мешает вам «убрать логарифмы». Что можно сделать с ним, чтобы в левой и правой частях были просто логарифмы по основанию 5? Для этого поможет формула для логарифма степени.

;

;

;

4. Решите уравнение: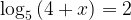

ОДЗ (Область допустимых значений): Значит,

Представим 2 в правой части уравнения как .

Функция 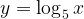монотонно возрастает и каждое свое значение принимает ровно один раз.

Логарифмы равны, их основания равны. «Уберем» логарифмы.

Плучим .

.

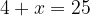
Ответ: 21.

5. Решите уравнение:

Испольуя равнозначные преобразования . Записываем ОДЗ и «скрываем» логарифмы:

Ответ: –4.

Решения логарифмических уравнений лучше всего записывать в виде цепочки равнозначных преобразований

6.Решите уравнение: .

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2.

Используя формулу перехода к другому основанию:

Запишем решение как цепочку разнозначных переходов.

Ответ: 19.

7.Решите уравнение: .

Следует помнить, что основание логарифма должно быть положительно и не равно 1.

Облать допустимых значений:

Теперь можно избавиться от логарифмов.

— корений не входит в ОДЗ, нарушая .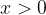

Ответ: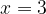

8. Решите уравнение .

ОДЗ уравнения: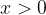

Используя замену .

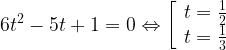
Вернемся к переменной х:

9.Решите уравнение:

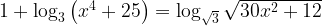
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25.

Выражение под корнем в правой части также положительно.

Значит, х ОДЗ - любое действительное число.

Используя формулу сумм логарифмов в левой части как логарифм произведения.

В правой части – перейдем к логарифму по основанию 3.

Применяя формулу логарифма степени.

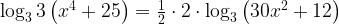
«скроем» логарифмы.

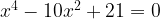
это биквадратное уравнение. Сделаем замену

Вернемся к переменной х. Получим:

.

Ответ: .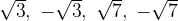

Вау!! 😲 Ты еще не читал? Это зря!

• логарифм
• уравнения , неравенства , переменные , выражения ,
• Логарифмические неравенства

Исследование, описанное в статье про логарифмические уравнения, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое логарифмические уравнения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра

Из статьи мы узнали кратко, но содержательно про логарифмические уравнения