Логарифмы определения и свойства, история и применение

Привет, сегодня поговорим про логарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое логарифм, применение логарифма, история логарифма , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.

Определение: логарифм ом положительного числа b по основанию 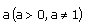называется показатель степени с, в которую надо возвести число а, чтобы получить число b.

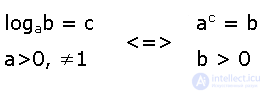
Основное логарифмическое тождество:

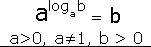
Свойства логарифмов:

Основное логарифмическое тождество

Из определения логарифма следует основное логарифмическое тождество[7]:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если

, то , откуда, согласно основному тождеству: .

Основное логарифмическое тождество

Из определения логарифма следует основное логарифмическое тождество[7]:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если , то , откуда, согласно основному тождеству: .

Исторический очерк

Предшественники

Идейным источником и стимулом применения логарифмов послужил тот факт (известный еще Архимеду[26]), что при перемножении степеней их показатели складываются[27]: . Индийский математик VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4[28].

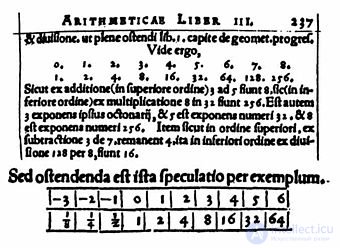
Логарифмическая таблица М. Штифеля, «Arithmetica integra», 1544

Решающий шаг был сделан в средневековой Европе. Потребность в сложных расчетах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоемкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной[26]. Тогда и деление автоматически заменяется на неизмеримо более простое и надежное вычитание, упростятся также возведение в степень и извлечение корня.

Первым эту идею опубликовал в своей книге «Arithmetica integra» (1544) Михаэль Штифель, который, впрочем, не приложил серьезных усилий для практической реализации своей идеи[29][30]. Главной заслугой Штифеля является переход от целых показателей степени к произвольным рациональным[31] (первые шаги в этом направлении сделали Николай Орем в XIV веке и Никола Шюке в XV веке).

Джон Непер и его «удивительная таблица логарифмов»

Джон Непер

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Descriptio). В нем было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Constructio), изданной посмертно в 1619 году его сыном Робертом.

Судя по документам, техникой логарифмирования Непер владел уже к 1594 году[32]. Непосредственной целью ее разработки было облегчить Неперу сложные астрологические расчеты[33]; именно поэтому в таблицы были включены только логарифмы тригонометрических функций.

Понятия функции тогда еще не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение; например, логарифм синуса он определил следующим образом[34]:

Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать.

В современных обозначениях кинематическую модель Непера можно изобразить дифференциальным уравнением[35]:

,

где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда еще не нашли широкого применения). Непер взял M = 10 000 000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию , то она связана с натуральным логарифмом следующим образом[35]:

Очевидно, , то есть логарифм «полного синуса» (соответствующего 90°) есть нуль — этого и добивался Непер своим определением. Также он хотел, чтобы все логарифмы были положительны; нетрудно убедиться, что это условие для выполняется. .

Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма, например:

Дальнейшее развитие

Как вскоре обнаружилось, из-за ошибки в алгоритме все значения таблицы Непера содержали неверные цифры после шестого знака[36]. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики. Кеплер в изданный им астрономический справочник 1620 года вставил восторженное посвящение Неперу (не зная, что изобретатель логарифмов уже скончался). В 1624 году Кеплер опубликовал свой собственный вариант логарифмических таблиц (лат. Chilias Logarithmorum ad totidem numeros rotundos)[37]. Использование логарифмов позволило Кеплеру относительно быстро завершить многолетний труд по составлению Рудольфинских таблиц, которые закрепили успех гелиоцентрической астрономии.

Спустя несколько лет после книги Непера появились логарифмические таблицы, использующие более близкое к современному понимание логарифма. Об этом говорит сайт https://intellect.icu . Лондонский профессор Генри Бригс издал 14-значные таблицы десятичных логарифмов (1617), причем не для тригонометрических функций, а для произвольных целых чисел до 1000 (7 лет спустя Бригс увеличил количество чисел до 20000). В 1619 году лондонский учитель математики Джон Спайделл (англ. John Speidell) переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов. У Спайделла тоже были и логарифмы самих чисел до 1000 (причем логарифм единицы, как и у Бригса, был равен нулю) — хотя масштабирование до целых чисел Спайделл сохранил[38][39].

Вскоре выяснилось, что место логарифмов в математике не ограничивается расчетными удобствами. В 1629 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой меняется по логарифмическому закону[40]. В 1668 году немецкий математик Николас Меркатор (Кауфман) открыл и опубликовал в своей книге Logarithmotechnia разложение логарифма в бесконечный ряд[41]. По мнению многих историков, появление логарифмов оказало сильное влияние на многие математические концепции, в том числе:

1. Формирование и признание общего понятия иррациональных и трансцендентных чисел[42].
2. Появление показательной функции и общего понятия числовой функции, числа Эйлера, развитие теории разностных уравнений[43].
3. Начало работы с бесконечными рядами[41].
4. Общие методы решения дифференциальных уравнений различных типов.
5. Существенное развитие теории численных методов, требуемых для вычисления точных логарифмических таблиц.

До конца XIX века общепринятого обозначения логарифма не было, основание a указывалось то левее и выше символа log, то над ним. В конечном счете математики пришли к выводу, что наиболее удобное место для основания — ниже строки, после символа log: . Краткие обозначения наиболее употребительных видов логарифма — для десятичного и натурального — появились намного раньше сразу у нескольких авторов и закрепились окончательно также к концу XIX века[44].

Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса (1685) и Иоганна Бернулли (1694), а окончательно было узаконено Эйлером[36]. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привел разложение их в степенные ряды, особо отметил роль натурального логарифма[45]. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Расширение логарифма на комплексную область

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда еще не было ясно определено само понятие логарифма[46]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить , в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число[46]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной[47]. Хотя спор продолжался (Д’Аламбер отстаивал свою точку зрения и подробно аргументировал ее в статье своей «Энциклопедии» и в других трудах), подход Эйлера к концу XVIII века получил всеобщее признание.

В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[48], определяемой как интеграл от . Риман, опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей.

Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая еще до открытия логарифмов (1550), может быть описана как комплексный логарифм[49].

Некоторые практические применения

Логарифмические зависимости в науке и природе

Логарифмические функции распространены чрезвычайно широко как в математике, так и в естественных науках. Часто логарифмы появляются там, где проявляется самоподобие, то есть некоторый объект последовательно воспроизводится в уменьшенном или увеличенном масштабе; см. ниже такие примеры, как рекурсивные алгоритмы, фракталы или раковины моллюсков. Приведем несколько примеров использования логарифмов в разнообразных науках.

Теория чисел

Распределение простых чисел асимптотически подчиняется простым законам[50]:

1. Число простых чисел в интервале от 1 до приблизительно равно .
2. k-е простое число приблизительно равно .

Еще более точные оценки используют интегральный логарифм.

Нередко возникает задача грубо оценить очень большое число — например, факториал или число Мерсенна с большим номером. Для этого было бы удобно приближенно записать число в экспоненциальном формате, то есть в виде мантиссы и десятичного порядка.

Задача легко решается с применением логарифмов. Рассмотрим для примера 44-е число Мерсенна .

Следовательно, мантисса результата равна { Окончательно получим:

Математический анализ

Вау!! 😲 Ты еще не читал? Это зря!: Список интегралов от логарифмических функций

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:

Теория вероятностей и статистика

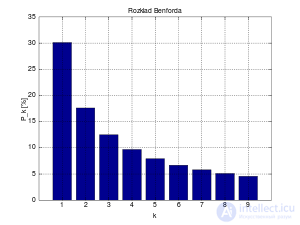
Распределение Бенфорда. По горизонтали — первые значащие цифры, по вертикали — вероятность их появления.

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение[51] используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных[52].

Закон Бенфорда (« закон первой цифры ») описывает вероятность появления определенной первой значащей цифры при измерении реальных величин.

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия[53].

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова.

Информатика и вычислительная математика

В информатике: единица измерения информации ( бит ). Например, для хранения в компьютере натурального числа (в обычном для компьютера двоичном формате) понадобится битов.

Информационная энтропия — мера количества информации.

Оценка асимптотической сложности рекурсивных алгоритмов, основанных на принципе «разделяй и властвуй»[54] — таких как быстрая сортировка , быстрое преобразование Фурье и т. п.

Обычно числовые значения хранятся в памяти компьютера или специализированного процессора в формате с плавающей запятой. Если, однако, сложение и вычитание для группы данных выполняются редко, а умножение, деление, возведение в степень и извлечение корня — гораздо чаще, тогда имеет смысл рассмотреть возможность хранения таких данных в логарифмическом формате. В этом случае вместо числа хранится логарифм его модуля и знак, и скорость вычислений благодаря свойствам логарифма значительно повышается[55]. Логарифмический формат хранения был использован в нескольких системах, где доказал свою эффективность[56][57].

Фракталы и размерность

Треугольник Серпинского (справа)

Логарифмы помогают выразить размерность Хаусдорфа для фрактала[58]. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

Механика и физика

Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень ее хаотичности.

Формула Циолковского применяется для расчета скорости ракеты.

Химия и физическая химия

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Теория музыки

Чтобы решить вопрос о том, на сколько частей делить октаву, требуется отыскать рациональное приближение для . Если разложить это число в непрерывную дробь, то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов[59].

Психология и физиология

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула[60] — громкости звука[61], яркости света.

Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется[62].

Время на принятие решения при наличии выбора можно оценить по закону Хика[en][63].

Биология

Ряд биологических форм хорошо соответствует логарифмической спирали[64] — кривой, у которой касательная в каждой точке образует с радиус-вектором в этой точке один и тот же угол , то есть прирост радиуса на единицу длины окружности постоянен:

Раковина наутилуса

Расположение семян на подсолнечнике

Цветная капуста Романеско

Разное

Число кругов игры по олимпийской системе равно двоичному логарифму от числа участников соревнований, округленному до ближайшего большего целого[65].

Логарифмическая шкала

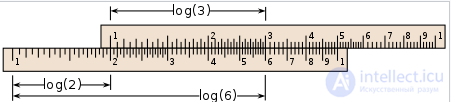
Логарифмическая шкала

Неравномерная шкала десятичных логарифмов используется во многих областях науки. Для обеспечения вычислений она наносится на логарифмические линейки. Другие примеры:

• Акустика — уровень звукового давления и интенсивность звука (децибелы)[66].
• Отношение сигнал /шум в радиотехнике и электросвязи[67].
• Астрономия — шкала яркости звезд[68].
• Химия — активность водородных ионов (pH)[69].
• Сейсмология — шкала Рихтера[70].
• Оптическая плотность — мера поглощения света прозрачными объектами или отражения света непрозрачными объектами[71].
• Фотографическая широта — характеристика светочувствительного материала[72].
• Шкала выдержек и диафрагм в фотографии[73].
• Теория музыки — нотная шкала, по отношению к частотам нотных звуков[59].
• Сельское хозяйство — основная гидрофизическая характеристика почвы[74].
• Теория управления — логарифмическая амплитудно-фазовая частотная характеристика [75].

Логарифмическая шкала особенно удобна в тех случаях, когда уровни измеряемой величины образуют геометрическую прогрессию, поскольку тогда их логарифмы распределены с постоянным шагом. Например, 12 полутонов классической октавы образуют (приближенно) такую прогрессию[59] со знаменателем . Аналогично, каждый уровень шкалы Рихтера соответствует в 10 раз большей энергии, чем предыдущий уровень. Даже при отсутствии геометрической прогрессии логарифмическая шкала может пригодиться для компактного представления широкого диапазона значений измеряемой величины.

Логарифмическая шкала также широко применяется для оценки показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой , более простой для исследования.

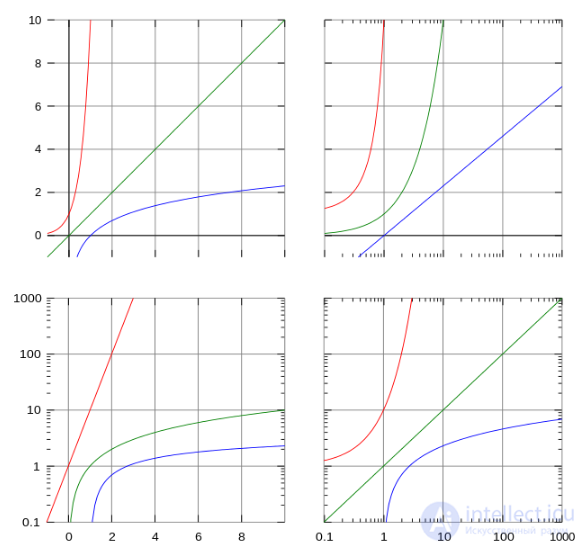
Графики трех функций при различном выборе шкал по осям координат:
Верхний ряд - 1) обе линейные ; 2) логарифмическая (x) и линейная (y);
Нижний ряд - 1) линейная (x) и логарифмическая (y); 2) обе логарифмические.

Логарифмические таблицы

Логарифмические таблицы

Из свойств логарифма следует, что вместо трудоемкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам (раздел «Антилогарифмы») выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются.

Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причем с ошибками. Независимо от него свои таблицы опубликовал Йост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки . Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера)[76].

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[77]. В СССР выпускались несколько сборников таблиц логарифмов[78]:

1. Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчетах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчетные инструменты.
2. Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
3. Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Классические шестизначные таблицы, удобные для расчетов с тригонометрическими функциями.
4. Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
5. Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука , 1971.
6. Десятизначные таблицы логарифмов комплексных чисел. М., 1952.

Логарифмическая линейка

Логарифмическая линейка

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов служившую незаменимым расчетным орудием инженера[79]. С помощью этого компактного инструмента можно быстро производить все алгебраические операции, в том числе с участием тригонометрических функций[80]. Точность расчетов — около 3 значащих цифр.

Логарифмическая линейка. Умножение 1,3 × 2 или деление 2,6 / 2 (см. шкалы C и D).

Вариации и обобщения

Логарифм как решение уравнения можно определить не только для вещественных и комплексных чисел.

• Можно ввести логарифмическую функцию для кватернионов (см. функции кватернионного переменного). Однако большинство алгебраических свойств логарифма при этом теряется[81] — например, логарифм произведения не равен сумме логарифмов, и это снижает практическую ценность такого обобщения .
• Если — элементы конечной абелевой мультипликативной группы, то логарифм в указанном смысле (если он существует) называется дискретным. Чаще всего он рассматривается для конечной группы кольца вычетов по некоторому модулю, где называется индексом по этому модулю[82] и играет важную роль в криптографии. В циклических группах логарифм существует, если его основание является первообразным корнем этой группы.
• Матричный логарифм[en]: можно определить логарифмы также для матриц[83].
• Можно определить p-адический логарифм[en] для некоторых p-адических чисел[84].
• Для работы с очень большими числами вводится понятие суперлогарифма, связанное не с возведением в степень, а с операцией более высокого порядка: тетрацией.

Я что-то не договорил про логарифм, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое логарифм, применение логарифма, история логарифма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА