Формулы сокращенного умножения кратко

формулы сокращенного умножения — это набор алгебраических тождеств, позволяющих упрощать вычисления и преобразовывать выражения без непосредственного выполнения умножения в полной форме. Эти формулы широко используются в алгебре для упрощения выражений, факторизации и решения уравнений.

Вот основные формулы сокращенного умножения:

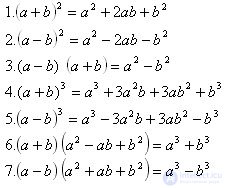
Эти формулы помогают быстрее и точнее решать задачи, особенно при упрощении выражений или подготовке к факторизации.

История формул сокращенного умножения

Формулы сокращенного умножения имеют древние корни и уходят в глубокую древность, когда математика только формировалась как наука.

Античные и классические времена:
Вавилон и Индия — более 2000 лет назад математики использовали примитивные формы этих тождеств, особенно квадрат суммы и разность квадратов, при работе с геометрическими задачами и площадями.

Евклид (ок. 300 г. до н. э.) — в своих «Началах» он описывает геометрические доказательства аналогов этих формул: например, (a + b)² как площади большого квадрата.

Индийский математик Брахмагупта (VII в.) использовал алгебраические тождества для упрощения вычислений.

Средние века и эпоха Возрождения:
Арабские математики (Аль-Хорезми и др.) активно использовали формулы при разработке алгебры.

В Европе, благодаря переводу арабских текстов на латынь, эти формулы вошли в университетское преподавание в XIII–XIV вв.

Современное время:
Систематический вид формулы получили в XVII–XVIII вв., когда алгебра стала строго формализованной наукой.

Рене Декарт и Исаак Ньютон использовали их в аналитической геометрии и при разработке математического анализа.

Применение формул сокращенного умножения

Эти формулы широко используются во многих областях математики и прикладных дисциплинах:

1. Школьная и университетская математика
Упрощение выражений.

Решение уравнений.

Факторизация многочленов.

2. Алгебра и математический анализ
Быстрое преобразование выражений в доказательствах.

Работа с пределами, производными и интегралами.

3. Геометрия и тригонометрия
Вычисления длин, площадей и объемов.

Использование площадей в формулах, особенно при работе с квадратами и кубами.

4. Физика и инженерия
Вычисления кинетической энергии, моментов инерции и других физических величин.

Упрощение формул при моделировании процессов.

5. Информатика
Символьные вычислительные алгоритмы.

Оптимизация кода, особенно в численных методах.

6. Экономика и статистика
Модели прогнозирования.

Анализ вариации и дисперсии (формулы типа (a − b)² встречаются в формулах расчета дисперсии).

6. Логика и развитие
развитие логического и модульного мышления.