Лекция
Привет, Вы узнаете о том , что такое тригонометрические функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое тригонометрические функции, синус, косинус, тангенс, котангенс , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.
тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
прямые тригонометрические функции:
производные тригонометрические функции:
обратные тригонометрические функции:
В типографике литературы на разных языках сокращенное обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются ,
,
. До Второй мировой войны в Германии и во Франции эти функции обозначались так же, как принято в русскоязычных текстах , но потом в литературе на языках этих стран был принят англоязычный вариант записи тригонометрических функций.
Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счетного числа разрывов второго рода: у тангенса и секанса в точках , а у котангенса и косеканса — в точках
.
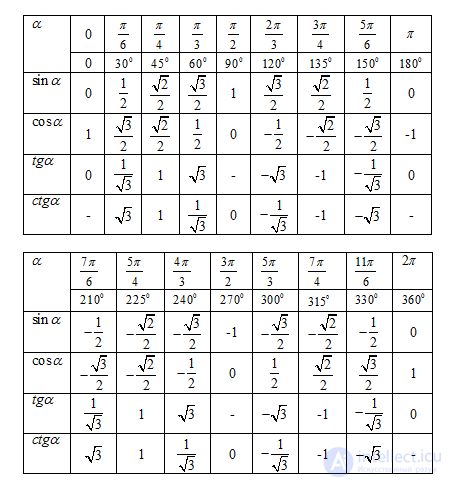
Графики тригонометрических функций показаны на рис. 1.

Косинусоида
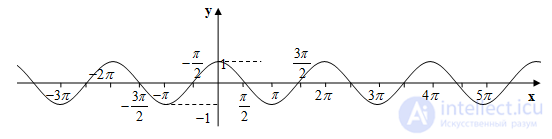
Синусоида

Тангенсоида
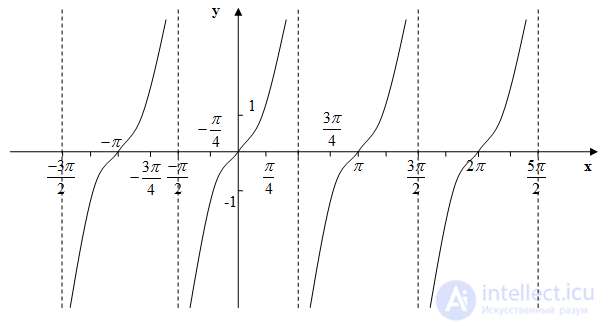
Котангенсоида
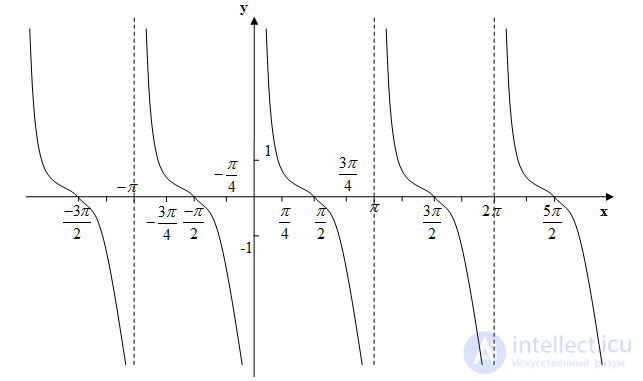
Изобретение способа измерения углов в градусах относится к III - II тысячелетиям до н.э. Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Об этом говорит сайт https://intellect.icu . Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Древнегреческие ученые не знали современных обозначений тригонометрических функций, вместо синуса они пользовались хордой. Греческое слова "хорда", означает "тетива лука". Первые таблицы хорд дошли до нас в книге Птолемея "Альмагест" (II в. н.э.)
В Индии, в трактате математики Ариабхата, в 499 г. встречаются функции синус, косинус и синусверсус. Они рассматривались только для острого угла.
Новые тригонометрические функции, которыми мы пользуемся и сейчас, были введены учеными стран Среднего и Ближнего Востока в IX - X вв. Понтяие "тангенс" и "котангенс", как и первые таблицы этих новых тригонометрических величин, родились из учения о солнечных часах (гномоники). Солнечные часы представляли собой шест, вертикально воткнутый в землю. Время отсчитывалось по длине и направлению тени, отбрасываемой шестом. Циферблатом служила площадка с колышками, вбитыми в землю.
Всего тригонометрических величин шесть: синус, косинус, тангенс, котангенс, секанс, косеканс.
В Европе первым трудом, в котором тригонометрия рассматривалась как самостоятельная ветвь математики, была работа немецкого астронома и математика Региомонтана "Пять книг о треугольниках всех видов", написанная в 1462 - 1466 гг. В ней автор систематизировал и изложил все известные к этому времени знания по тригонометрии.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
В1770 г. появилось и удерживается до наших дней название Тригонометрические функции. Его ввел Г. С. Клюгель в работе “Аналитическая тригонометрия”.
Наиболее значимые исследования по тригонометрии связаны с именами Насирэддина Туси (1201 - 1274), Джона Валлиса (1616 - 1703), Джеймса Грегори (1638 - 1675), Исаака Барроу (1630 - 1677), Роджера Котеса (1682 - 1716), Исаака Ньютона (1643 - 1727), Леонарда Эйлера (1707 - 1783).
Линия синуса (линия на рис. 2) у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды данной дуги, поскольку дуга с хордой напоминает лук с тетивой). Затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские математики, переводя индийские книги с санскрита, не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали его арабскими буквами и стали называть линию синуса «джиба» (جيب). Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса как «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus — «синус», имеющим то же значение (именно в этом значении оно применяется как анатомический термин синус). Термин «косинус» (лат. cosinus) — это сокращение от лат. complementi sinus — дополнительный синус.
Современные краткие обозначения ,
введены Уильямом Отредом и Бонавентурой Кавальери и закреплены в трудах Леонарда Эйлера.
Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введен Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчетов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.
Геодезия
Древняя астрономия
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» дает подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.

Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест),
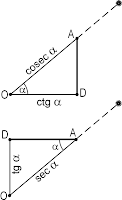
Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчета солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Архитектура
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось
Ситуация меняется , так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу
Медицина и биология.
Модель боритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея "измерения углов" не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс
вновь позабыли.
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму
Измерительные работы
С=180-а-b, sinC=sin(180-a-b)=sin(a+b)
Затем с помощью теоремы синусов находим d.
Вычислительный интеллект и машинное обучение
Использование активационной функции в виде линейного порога расширяет область значений выхода нейрона, но при этом он все еще остается линейным преобразователем, что значительно снижает аппроксимирующие возможности сети. Кроме этого, наличие двух точек разрыва, где функция не дифференцируема, делает невозможным использование линейного порога в градиентных алгоритмах обучения, где используется производная активационной функции.
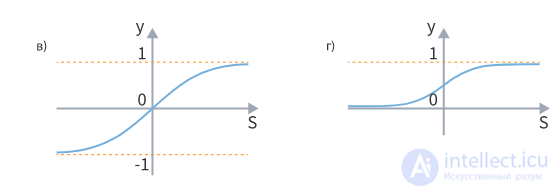
Поэтому при обучении многослойных нейронных сетей наиболее часто используются сигмоидальные активационные функции, названные так за их характерную S-образную форму. Примерами таких функций являются гиперболический тангенс (график (в) на рисунке) и логистическая функция (график (г)), задаваемые соответствующими формулами:
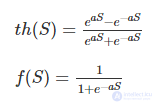
Это монотонно возрастающие функции, дифференцируемые на всей области определения, что делает их применимыми в алгоритмах обучения, использующих производные активационной функции. Обычно все нейроны сети имеют одинаковую активационную функцию.
Исследование, описанное в статье про тригонометрические функции, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое тригонометрические функции, синус, косинус, тангенс, котангенс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Комментарии
Оставить комментарий
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Термины: СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА