Лекция
Сразу хочу сказать, что здесь никакой воды про тригонометрия, и только нужная информация. Для того чтобы лучше понимать что такое тригонометрия, синус, косинус, тангенс, котангенс, арксинус, арукосинус, арктангенс, арккотангенс , настоятельно рекомендую прочитать все из категории Алгебра.
тригонометрия (от греческого trigōnon , «треугольника» и Metron , «меры» ) является разделом математики , которая изучает взаимосвязь между длинами сторон и углами зрения треугольников . Эта область возникла в эллинистическом мире в 3 веке до н.э. из приложений геометрии к астрономическим исследованиям . Греки сосредоточились на вычислении хорд , в то время как математики в Индии создали самые ранние известные таблицы значений для тригонометрических соотношений (также называемых тригонометрическими функциями ), такие как синус .
На протяжении всей истории тригонометрия применялась в таких областях, как геодезия , геодезия , небесная механика и навигация .
Тригонометрия известна своими многочисленных идентичностей , , которые представляют собой уравнение , используемое для перезаписи тригонометрических выражений для решения уравнений, чтобы найти более полезное выражение, или открыть для себя новые отношений.

Гиппарх , которому приписывают составление первой тригонометрической таблицы , был описан как «отец тригонометрии».
Шумерские астрономы изучали измерение углов, используя разделение окружностей на 360 градусов. Они, а позже и вавилоняне , изучили отношения сторон подобных треугольников и обнаружили некоторые свойства этих соотношений, но не превратили это в систематический метод нахождения сторон и углов треугольников. В древних нубийцев использовали подобный метод.
В III веке до нашей эры эллинистические математики, такие как Евклид и Архимед, изучали свойства хорд и вписанных углов в окружности, и они доказали теоремы, эквивалентные современным тригонометрическим формулам, хотя они представили их геометрически, а не алгебраически. В 140 г. до н.э. Гиппарх (из Никеи , Малая Азия) дал первые таблицы аккордов, аналогичные современным таблицам значений синусов , и использовал их для решения задач тригонометрии и сферической тригонометрии . Во 2 веке нашей эры греко-египетский астроном Птолемей(из Александрии, Египет) построил подробные тригонометрические таблицы ( таблица аккордов Птолемея ) в Книге 1, главе 11 своего Альмагеста . Птолемей использовал длину хорды для определения своих тригонометрических функций, что незначительно отличается от синусоидального соглашения, которое мы используем сегодня. (Значение, которое мы называем sin (θ), можно найти, посмотрев длину хорды для удвоенного угла интереса (2θ) в таблице Птолемея, а затем разделив это значение на два.) Прошли столетия, прежде чем были составлены более подробные таблицы. и трактат Птолемея продолжал использоваться для выполнения тригонометрических вычислений в астрономии в течение следующих 1200 лет в средневековой византийской , исламской, а затем и западноевропейские миры.
Современное синусоидальное соглашение впервые засвидетельствовано в Сурья-сиддханте , а его свойства были дополнительно задокументированы индийским математиком и астрономом 5-го века (н.э.) Арьябхатой . Эти греческие и индийские труды были переведены и дополнены средневековыми исламскими математиками . К 10 веку исламские математики использовали все шесть тригонометрических функций, составили таблицы своих значений и применяли их к задачам сферической геометрии . персидский эрудит Насир ад-Дин ат-Туси был описан как создатель тригонометрии как математической дисциплины в своем собственном праве. Насир ад-Дин ат-Туси был первым, кто стал рассматривать тригонометрию как математическую дисциплину, независимую от астрономии, и развил сферическую тригонометрию в ее нынешней форме. Он перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии, а в своей работе « О секторном рисунке» сформулировал закон синусов для плоских и сферических треугольников, открыл закон касательных для сферических треугольников и представил доказательства обоих этих законов. Знания о тригонометрических функциях и методах достигли Западной Европы через латинский перевод греческого Альмагеста Птолемея.а также работы персидских и арабских астрономов, таких как Аль Баттани и Насир ад-Дин ат-Туси . Одна из самых ранних работ по тригонометрии по северной европейской математике является De Triangulis в 15 - м веке немецкого математик Regiomontanus , который поощрял к записи, и снабженная копией Альмагеста , по византийскому греческому ученому кардиналу Виссарион Никейского с которым он прожил несколько лет. В то же время критяне завершили еще один перевод Альмагеста с греческого на латынь.Георгий Трапезундский . Тригонометрия была еще так мало известна в Северной Европе 16-го века, что Николай Коперник посвятил две главы De Revolutionibus orbium coelestium объяснению ее основных понятий.
Из-за требований навигации и растущей потребности в точных картах больших географических областей тригонометрия превратилась в важную отрасль математики. Варфоломей Питискус был первым, кто использовал это слово, опубликовав свою « Тригонометрию» в 1595 году. Джемма Фризиус впервые описала метод триангуляции, который до сих пор используется в геодезической съемке. Это был Leonhard Euler , которые полностью включены в комплексные числа в тригонометрии. Работы шотландских математиков Джеймса Грегори в 17 веке и Колина Маклоренав 18 веке оказали влияние на развитие тригонометрических рядов Также в 18 веке Брук Тейлор определил общий ряд Тейлора .

Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии» .
Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на нее хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме. Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sinα/sinβ < α/β < tgα/tgβ, где 0° < β < α < 90°, совместно с другими теоремами.
Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свел в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.
Менелай Александрийский (100 н. э.) написал «Сферику» в трех книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».
Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырехугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93-е предложение «Данных» Евклида.
Теорема Птолемея влечет за собой эквивалентность четырех формул суммы и разности для синуса и косинус а. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха.
Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
Индийцы также знали формулы для кратных углов где
Тригонометрия необходима для астрономических расчетов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее ученые составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.
Южноиндийские математики в XVI веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арк тангенс а в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати[en]» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенс а был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.
С VIII века ученые стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX века среднеазиатский ученый аль-Хорезми написал сочинение «Об индийском счете». После того как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки.

В этом прямоугольном треугольнике: sin A = a / c ; cos A = b / c ; загар А = а / б .
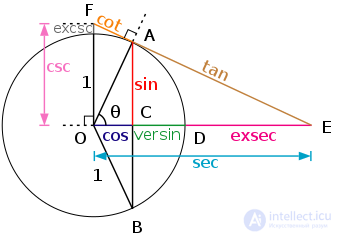
Тригонометрические функции угла θ внутри единичной окружности
Тригонометрические отношения - это отношения между сторонами прямоугольного треугольника. Эти соотношения задаются следующими тригонометрическими функциями известного угла A , где a , b и c относятся к длинам сторон на прилагаемом рисунке:
Гипотенузой является стороной , противоположной углом 90 градусов в прямоугольном треугольнике; это самая длинная сторона треугольника и одна из двух сторон , примыкающих к углу А . Смежно нога другая сторона , которая находится рядом с углом А . Сторона , противоположная сторона , которая находится напротив угла А . Термины « перпендикуляр» и « основание» иногда используются для обозначения противоположных и смежных сторон соответственно. См. Ниже в разделе « Мнемоника» .
Так как любые два прямоугольных треугольников с одинаковым углом острого A являются подобны , значение тригонометрического соотношения зависит только от угла A .
В обратных этих функциях названы косеканс (CSC), секущие (сек) и котангенс (раскладушка), соответственно:
Косинус, котангенс и косеканс названы так, потому что они, соответственно, являются синусом, тангенсом и секансом дополнительного угла, сокращенного до «со-».
С помощью этих функций можно ответить практически на все вопросы о произвольных треугольниках, используя закон синусов и закон косинусов Эти законы могут быть использованы для вычисления оставшихся углов и сторон любого треугольника, если известны две стороны и их угол или два угла, а также сторона или три стороны.
Мнемоника в тригонометрии
Обычно мнемоника используется для запоминания фактов и взаимосвязей в тригонометрии. Например, отношения синуса , косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их и их соответствующие стороны в виде цепочек букв. Об этом говорит сайт https://intellect.icu . Например, мнемоника SOH-CAH-TOA:
S ине = O pposite ÷ Н ypotenuse
C osine = A djacent ÷ H ypotenuse
Т angent = O pposite ÷ djacent
Один из способов запомнить буквы, чтобы звук их фонетически (т.е. SOH-CAH-TOA , которое произносится «так KÀ- носком -uh» / s oʊ к æ т oʊ ə / ). Другой способ заключается в расширении буквы в предложении, такие как « S OMe O LD Н ippie С нечто ругой Н ippie Т rippin' О п ИДС».

Рис. 1a - Синус и косинус угла θ, определенного с помощью единичной окружности.
Тригонометрические отношения также могут быть представлены с помощью единичной окружности , которая представляет собой окружность радиуса 1 с центром в начале координат на плоскости. В этой настройке конечная сторона угла A, помещенного в стандартное положение, будет пересекать единичный круг в точке (x, y), где а также
. Это представление позволяет вычислять часто встречающиеся тригонометрические значения, например, в следующей таблице:
| Функция | 0 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| синус | 0 | 1 | 0 | ||||||
| косинус | 1 | 0 | -1 | ||||||
| касательная | 0 | неопределенный | 0 | ||||||
| секущий | 1 | неопределенный | -1 | ||||||
| косеканс | неопределенный | 1 | неопределенный | ||||||
| котангенс | неопределенный | 0 | неопределенный |
Используя единичный круг , можно расширить определения тригонометрических отношений на все положительные и отрицательные аргументы (см. Тригонометрическую функцию ).
В следующей таблице приведены свойства графиков шести основных тригонометрических функций: [37] [38]
| Функция | Период | Домен | Диапазон | График |
|---|---|---|---|---|
| синус |  |
|||
| косинус |  |
|||
| касательная |  |
|||
| секущий |  |
|||
| косеканс |  |
|||
| котангенс |  |
Поскольку шесть основных тригонометрических функций периодичны, они не инъективны (или 1 к 1) и, следовательно, не обратимы. Однако, ограничив область определения тригонометрической функции, их можно сделать обратимыми.
Имена обратных тригонометрических функций вместе с их областями определения и диапазоном можно найти в следующей таблице:
| имя | Обычное обозначение | Определение | Домен x для реального результата | Диапазон обычного главного значения ( радианы ) |
Диапазон обычного главного значения ( градусы ) |
|---|---|---|---|---|---|
| арксинус | у = arcsin ( х ) | х = грех ( у ) | −1 ≤ х ≤ 1 | -π/2≤ y ≤π/2 | −90 ° ≤ y ≤ 90 ° |
| арккозин | у = arccos ( х ) | х = соз ( у ) | -1 ≤ х ≤ 1 | 0 ≤ у ≤ π | 0 ° ≤ y ≤ 180 ° |
| арктангенс | у = арктангенс ( х ) | х = загар ( у ) | все реальные числа | -π/2< у <π/2 | -90 ° < у <90 ° |
| арккотангенс | y = arccot ( x ) | x = детская кроватка ( y ) | все реальные числа | 0 < у < π | 0 ° < у <180 ° |
| арксеканс | y = arcsec ( x ) | х = сек ( у ) | x ≤ −1 или 1 ≤ x | 0 ≤ у <π/2 или π/2< у ≤ π | 0 ° ≤ y <90 ° или 90 ° < y ≤ 180 ° |
| аркосеканс | у = arccsc ( х ) | х = csc ( y ) | x ≤ −1 или 1 ≤ x | -π/2≤ y <0 или 0 < y ≤π/2 | −90 ° ≤ y <0 ° или 0 ° < y ≤ 90 ° |
Если рассматривать тригонометрические отношения как функции действительной переменной, их можно представить бесконечным рядом . Например, синус и косинус имеют следующие представления: [41]
С помощью этих определений тригонометрические функции могут быть определены для комплексных чисел . При расширении функции действительных или комплексных переменных для комплексной экспоненты справедлива следующая формула :
Эта сложная экспоненциальная функция, записанная в терминах тригонометрических функций, особенно полезна.
Тригонометрические функции были одними из первых применений математических таблиц . Такие таблицы были включены в учебники математики, и студентов учили искать значения и как интерполировать между перечисленными значениями, чтобы получить более высокую точность. У правил скольжения были специальные шкалы для тригонометрических функций.
В научных калькуляторах есть кнопки для вычисления основных тригонометрических функций (sin, cos, tan, а иногда и cis и их обратные). Большинство из них позволяют выбирать методы измерения углов: градусы , радианы, а иногда и градиенты . Большинство языков программирования предоставляют библиотеки функций, которые включают тригонометрические функции. модуль с плавающей запятой аппаратных средств включены в микропроцессорных чипов , используемых в большинстве персональных компьютеров имеет встроенные инструкции для вычисления тригонометрических функций.
В дополнение к шести коэффициентам, перечисленным ранее, существуют дополнительные тригонометрические функции, которые имели историческое значение, хотя сегодня редко используются. К ним относятся аккорд ( crd ( θ ) = 2 sin (θ/2) ) версина ( versin ( θ ) = 1 - cos ( θ ) = 2 sin 2 (θ/2) ) (который появился в самых ранних таблицах [51] ), покрывающая синусоида ( охватывает ( θ ) = 1 - sin ( θ ) = versin (π/2- θ ) ), гаверсинус ( haversin ( θ ) =1/2versin ( θ ) = sin 2 (θ/2) ) exsecant ( exsec ( θ ) = с ( θ ) - 1 ), а также excosecant ( excsc ( θ ) = exsec (π/2- θ ) = csc ( θ ) - 1 ). См. Список тригонометрических тождеств для получения дополнительных сведений о взаимосвязях между этими функциями.

Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C
В следующих тождествах, A, B и C являются углами треугольника; a, b, c — длины сторон треугольника, лежащие напротив соответствующих углов.
Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника
где — радиус окружности, описанной вокруг треугольника.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
или:
Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство:
где — основание натурального логарифма,
— мнимая единица. Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера:
с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением.
Если — вещественных решений нет.
Если — решением является число вида
Если — вещественных решений нет.
Если — решением является число вида
Решением является число вида
Решением является число вида
Важным частным разделом тригонометрии, используемым в астрономии, геодезии, навигации и других отраслях, является сферическая тригонометрия, рассматривающая свойства углов между большими кругами на сфере и дуг этих больших кругов. Геометрия сферы существенно отличается от евклидовой планиметрии; так, сумма углов сферического треугольника, вообще говоря, отличается от 180°, треугольник может состоять из трех прямых углов. В сферической тригонометрии длины сторон треугольника (дуги больших кругов сферы) выражаются посредством центральных углов, соответствующих этим дугам. Поэтому, например, сферическая теорема синусов выражается в виде
и существуют две теоремы косинусов, двойственные друг другу.
На протяжении веков сферическая тригонометрия использовалась для определения положения Солнца, Луны и звезд [53], предсказания затмений и описания орбит планет.
В наше время метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд [55], а также в системах спутниковой навигации . [16]

Секстанты используются для измерения угла солнца или звезд по отношению к горизонту. Используя тригонометрию и морской хронометр , можно определить положение корабля по таким измерениям.
Исторически тригонометрия использовалась для определения широты и долготы парусных судов, построения курсов и расчета расстояний во время навигации.
Тригонометрия по-прежнему используется в навигации с помощью таких средств, как глобальная система позиционирования и искусственный интеллект для автономных транспортных средств .
В земельной съемке , тригонометрия используется при расчете длины, площади и относительных углов между объектами. [58]
В более крупном масштабе тригонометрия используется в географии для измерения расстояний между ориентирами [59]


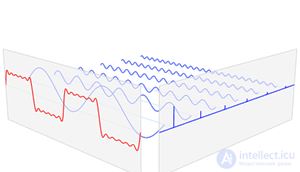
Функция (красный) - это сумма шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье,
(синим цветом), который отображает зависимость амплитуды от частоты, показывает 6 частот ( в нечетных гармониках ) и их амплитуды ( 1 / нечетное число ).
Функции синус и косинус имеют основополагающее значение для теории периодических функций , таких , как те , которые описывают звук и световые волны. Фурье обнаружил , что каждая непрерывная , периодическая функция может быть описана как бесконечная сумма тригонометрических функций.
Даже непериодические функции могут быть представлены как интеграл синусов и косинусов с помощью преобразования Фурье . Это имеет приложения , помимо других областей, в квантовой механике и коммуникации .
Основные статьи: Оптика и акустика
Тригонометрия полезно во многих физических науках , в том числе акустика и оптика . В этих областях они используются для описания звуковых и световых волн , а также для решения проблем, связанных с границами и передачей.
Другие области, которые используют тригонометрию или тригонометрические функции, включают теорию музыки , геодезию , синтез звука , архитектуру , электронику , биологию , медицинскую визуализацию ( компьютерная томография и ультразвук ), химия , теория чисел (и, следовательно, криптология ), сейсмология , метеорология , океанография , сжатие изображений , фонетика , экономика , электротехника , машиностроение , гражданское строительство , компьютерная графика , картография , кристаллография и разработка игр .

Треугольник со сторонами a , b , c и соответственно противоположными углами A , B , C
Тригонометрия известна своими многочисленными идентичностями, то есть уравнениями, которые верны для всех возможных входных данных. [80]
Тождества, включающие только углы, известны как тригонометрические тождества . Другие уравнения, известные как тождества треугольников , [81] связывают как стороны, так и углы данного треугольника.
В следующих тождествах A , B и C - углы треугольника, а a , b и c - длины сторон треугольника, противоположные соответствующим углам (как показано на диаграмме). [82]
Закон синусов
Закон синусов (также известный как «синус правила») для произвольного треугольника состояний: [83]
где - площадь треугольника, а R - радиус описанной окружности треугольника:
Закон косинусов
Закон косинусов (известно как формула косинуса, или «совы правило») является продолжением теоремы Пифагора на произвольные треугольниках: [83]
или эквивалентно:
Закон касательных
Закон касательных , разработанный Вьют , является альтернативой косинусов при решении по неизвестным краям треугольника, обеспечивая простые вычисления при использовании тригонометрических таблиц. [84] Это дает:
Площадь
Учитывая две стороны a и b и угол между сторонами C , площадь треугольника определяется как половина произведения длин двух сторон и синуса угла между двумя сторонами:
Формула Герона - еще один метод, который можно использовать для вычисления площади треугольника. Эта формула утверждает, что если треугольник имеет стороны длиной a , b и c , и если полупериметр равен
тогда площадь треугольника равна: [85]
,
где R - радиус описанной окружности треугольника.
Пифагорейские тождества
Следующие тригонометрические тождества связаны с теоремой Пифагора и верны для любого значения: [86]
Формула Эйлера
Формула Эйлера , которая утверждает, что, дает следующие аналитические тождества для синуса, косинуса и тангенса через e и мнимую единицу i :
Другие тригонометрические тождества
Другие часто используемые тригонометрические тождества включают тождества половинного угла, тождества суммы углов и разностей, а также тождества произведения к сумме. [29]
А как ты думаешь, при улучшении тригонометрия, будет лучше нам? Надеюсь, что теперь ты понял что такое тригонометрия, синус, косинус, тангенс, котангенс, арксинус, арукосинус, арктангенс, арккотангенс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгебра
Термины: Алгебра