Лекция
Привет, Вы узнаете о том , что такое обратные тригонометрические функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обратные тригонометрические функции, арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.
обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую ее хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика Карла Шерфера (нем. Karl Scherffer; 1716—1783) и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: но они не прижились . Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п. , — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.
Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, означает множество углов
, синус которых равен
. Из множества значений каждой аркфункции выделяют ее главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.
В общем случае при условии все решения уравнения {\displaystyle \sin x=\alpha }
можно представить в виде
Тригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и других.Евклида Архимеда В последующий период математика долгое время наиболее активно развивалась индийскими и арабскими учеными. В трудах по астрономии Ариабхаты появляется термин «ардхаджива». Позднее привилось более краткое название «джива», а при переводе математических терминов в XII в. Это слово было заменено латинским «sinus». Принципиальное значение имело составление Птолемеем первой таблицы синасов(долгое время она называлась таблицей хорд): появилось практическое средство решения ряда прикладных задач, и в первую очередь задач астрономии. Слово косинас –это сокращение латинского выражения «complementy sinus»(синас). Тататангенсы возникли в связи с решением задачи об определении длины тени.Тататангенс (а также котататангенс, сеганс и косеганс) введен в X веке Абу-л-Вафой, который составил и первые таблицы для нахождения тататангенсов и котататангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тататангенсы были заново открыты в XIV в. Т. Бравердином, а позже астрономом Региомонтаном. Первым автором, который использовал специальные символы для обратных тригонометрических функций был, Бернулли. В 1729 и в 1736 годах он писал as и at соответственно вместо arcsin и arctg.Современные обозначения arcsin и arctg появляются в 1772 г. в работах венского математика Шерфера известного французского ученого Лагранжа.Приставка «arc» происходит от латинского «arcus»(лук, дуга), что вполне согласуется со смыслом понятия: arcsin x, например,- это угол (а можно сказать и дуга) синас которого равен x
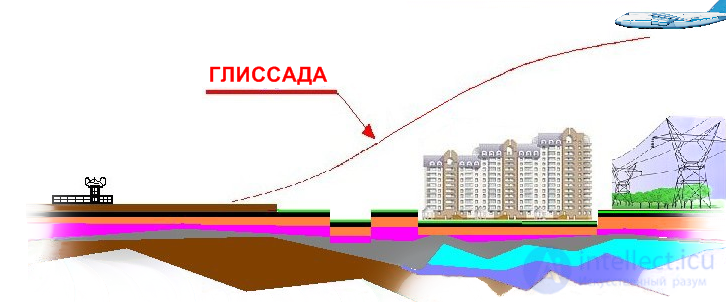

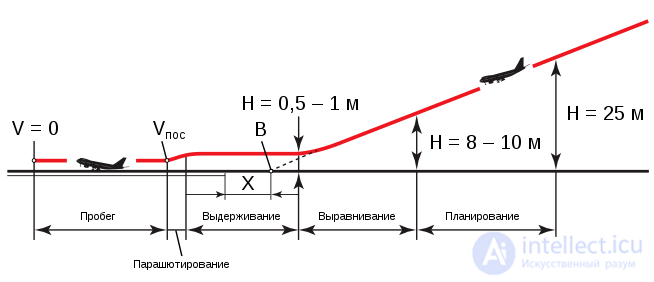
В первом приближении глиссада похожа на обратную тригонометрическую функцию типа арксинус или арктангенс( глиссада - траектория полета летательного аппарата (самолета, вертолета, планера, парашутиста), по которой он снижается, в том числе — непосредственно перед посадкой. ) конечно, для описания полета БЛА составляется более сложная пространственная математическая модель
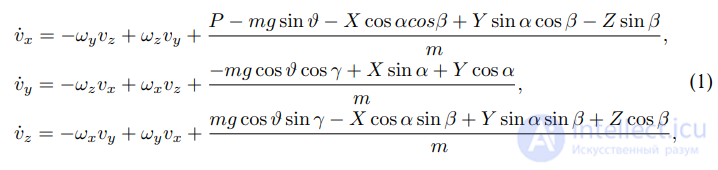
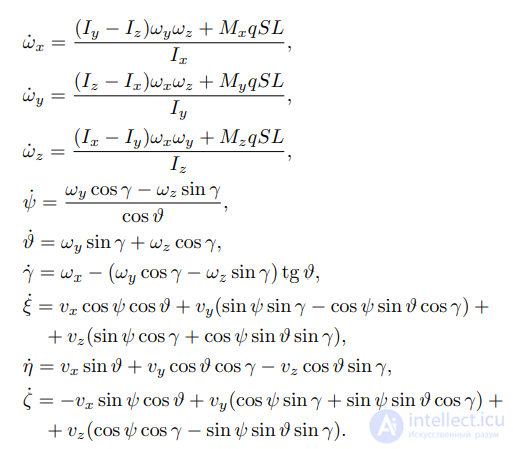
Здесь vx, vy, vz — проекции вектора скорости центра масс аппарата на оси связанной системы координат; ωx, ωy, ωz — проекции вектора угловой скорости БЛА на оси связанной системы координат; ξ, η, ζ — координаты центра масс беспилотника в локальной системе координат; α, β — углы атаки и скольжения БЛА. X, Y , Z — проекции вектора полной аэродинамической силы, действующей на БЛА, на оси воздушной системы координат: X — лобовое сопротивление, Y — подъемная сила, Z — боковая сила. g — ускорение свободного падения в районе ВПП, P — тяга, развиваемая пропеллером. Ix, Iy, Iz — главные моменты инерции БЛА (тензор инерции предполагается диагональным), q — скоростной напор набегающего потока, S — площадь крыльев, L — раз мах крыльев, bA — средняя аэродинамическая хорда; Mx, My, Mz — безразмерные коэффициенты моментов крена, рыскания и тангажа соответственно. К представленным дифференциальным уравнениям добавляются алгебраические соотношения


где v — воздушная скорость БЛА, Cx, Cy, Cz — безразмерные коэффициенты аэродинамических сил; δT S — угол отклонения руля высоты, δdir — угол отклонения руля направления, δflap — угол отклонения флаперонов (в симметричном режиме), δail — угол отклонения элеронов (в дифференциальном режиме).
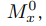
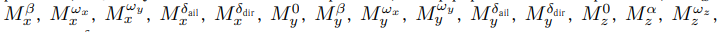
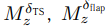 — заданные постоянные производные моментов крена, рыскания и тангажа.
— заданные постоянные производные моментов крена, рыскания и тангажа.
 — заданные постоянные коэффициенты аэродинамических сил.
— заданные постоянные коэффициенты аэродинамических сил.
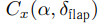 — некоторая заданная функция, которую будем считать линейной по δflap. Выпишем уравнения, которые моделируют поведение рулей высоты, направления и элеронов с запаздыванием, характеризующимся постоянной времени
— некоторая заданная функция, которую будем считать линейной по δflap. Выпишем уравнения, которые моделируют поведение рулей высоты, направления и элеронов с запаздыванием, характеризующимся постоянной времени
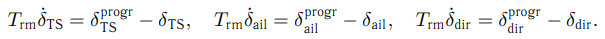 (15)
(15)
Полученная система (1), (15), дополненная соотношениями (2)—(14) и законами управления отклонением рулей, элеронов и флаперонов, будет полной и замкнутой.
Также При обучении многослойных нейронных сетей наиболее часто используются сигмоидальные активационные функции, названные так за их характерную S-образную форму. Примерами таких функций являются гиперболический тангенс (график (в) на рисунке) и логистическая функция (график (г)),
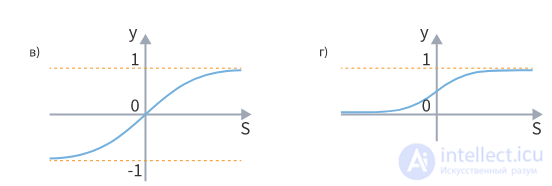
также визуально напоминающие обратные тригонометрические функции

График функции
Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений —
. Так как для функции
на интервале
каждое значение функции достигается при единственном значении аргумента, то на этом отрезке существует обратная функция
график которой симметричен графику функции
на отрезке
относительно прямой
(графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости
)
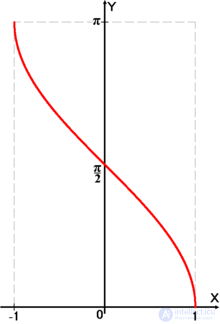
График функции
Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения —
На этом отрезке
строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке
существует обратная функция {\displaystyle y=\arccos x,}
график которой симметричен графику
на отрезке
относительно прямой {\displaystyle y=x.}

График функции
Аркта́нгенсом числа x называется такое значение угла выраженное в радианах, для которого
Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
функцией не является (так как нарушается требование однозначности). Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —
На этом отрезке {\displaystyle y=\operatorname
строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале
существует обратная
, график которой симметричен графику
на отрезке
относительно прямой

График функции
Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого
Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Об этом говорит сайт https://intellect.icu . Она является строго убывающей и всюду положительной.
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
функцией не является. Поэтому рассмотрим промежуток, на котором она строго убывает и принимает все свои значения только один раз —
. На этом отрезке
строго убывает и принимает все свои значения только один раз, следовательно, на интервале
существует обратная функция
, график которой симметричен графику {\displaystyle y=\operatorname
на отрезке
относительно прямой
График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, ) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы
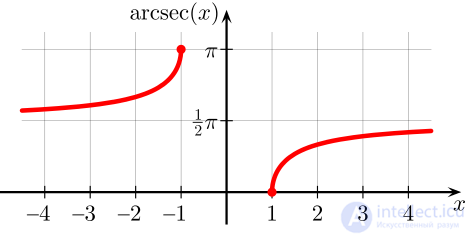
График функции
Арксекансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.
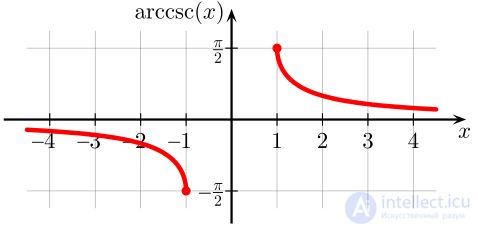
График функци
Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.
Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:

производные обратных тригонометрических функций
| Функция {\displaystyle f(x)} |
Производная {\displaystyle f'(x)} |
Примечание |
|---|---|---|
|
Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. |
||
| { |
Доказательство Найти производную арккосинуса можно при помощи данного тождества: |
|
|
Доказательство Найти производную арктангенса можно при помощи взаимнообратной функии: |
||
|
Доказательство Найти производную арккотангенса можно при помощи данного тождества: |
||
|
Доказательство Найти производную арксеканса можно при помощи тождества: Теперь находим производную обеих частей этого тождества. Получается. |
||
|
Доказательство Найти производную арккосеканса можна при помощи данного тождества: |
Для действительных и комплексных x:
Для действительных x ≥ 1:
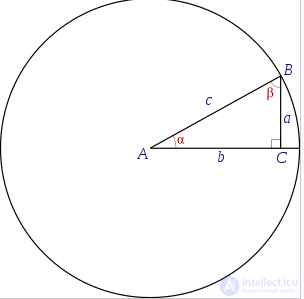
Прямоугольный треугольник ABC
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол. Так, если катет длины является противолежащим для угла
, то
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
Обратные тригонометрические функции полезны при попытке определить оставшиеся два угла прямоугольного треугольника, когда известны длины сторон треугольника. Вспоминая определения синуса и косинуса в прямоугольном треугольнике, следует, что
Часто гипотенуза неизвестна, и ее необходимо вычислить перед использованием арксинуса или арккосинуса с использованием теоремы Пифагора : куда
- длина гипотенузы. В этой ситуации может пригодиться арктангенс, поскольку длина гипотенузы не нужна.
Например, предположим, что крыша опускается на 8 футов, когда заканчивается на 20 футов. Крыша образует угол θ с горизонтом, где θ можно вычислить следующим образом:
Функция atan2 с двумя аргументами вычисляет арктангенс y / x с учетом y и x , но с диапазоном (- π , π ]. Другими словами, atan2 ( y , x ) - это угол между положительной осью x плоскость и точка ( x , y ) на ней, с положительным знаком для углов против часовой стрелки (верхняя полуплоскость, y > 0) и отрицательным знаком для углов по часовой стрелке (нижняя полуплоскость, y <0). Впервые он был представлен на многих языках программирования, но теперь он также широко используется в других областях науки и техники.
С точки зрения стандартной функции arctan , то есть с диапазоном (-π/2, π/2), его можно выразить следующим образом:
Оно также равно главное значение этого аргумента в комплексное число х + я у .
Эта функция также может быть определена с использованием следующих формул касательного полуугла :
при условии, что либо x > 0, либо y ≠ 0. Однако это не удается, если задано x ≤ 0 и y = 0, поэтому выражение непригодно для вычислительного использования.
Приведенный выше порядок аргументов ( y , x ) кажется наиболее распространенным и, в частности, используется в стандартах ISO, таких как язык программирования C , но некоторые авторы могут использовать противоположное соглашение ( x , y ), поэтому требуется некоторая осторожность. . Эти варианты подробно описаны на сайте atan2 .
Во многих приложениях [20] решение уравнения
должно быть как можно ближе к заданному значению
. Адекватное решение получается с помощью функции арктангенса с измененным параметром
Функция округляет до ближайшего целого числа.
Для углов, близких к 0 и π , арккосинус плохо обусловлен и, таким образом, будет вычислять угол с пониженной точностью в компьютерной реализации (из-за ограниченного количества цифр). [21] Аналогичным образом, арксинус неточен для углов, близких к - π / 2 и π / 2.
Традиционные способы решения уравнений с обратными тригонометрическими функциями (аркфункциями) сводятся к вычислению какой-нибудь тригонометрической функции от обеих частей с последующим преобразованием полученных суперпозиций по известным тригонометрическим формулам и формулам приведенных ниже:
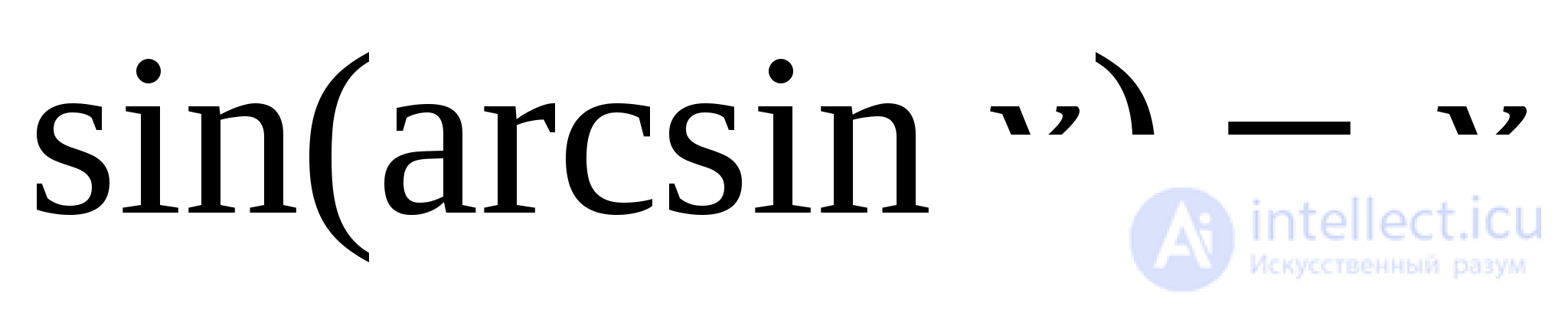
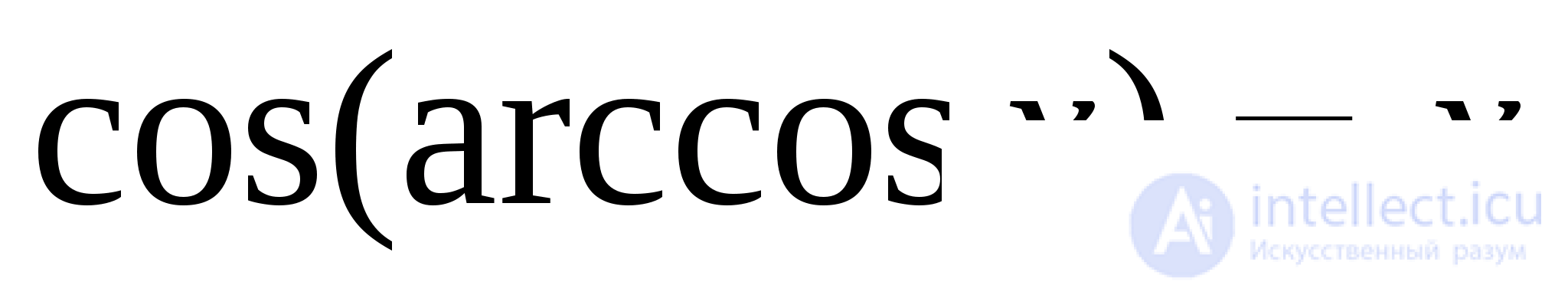
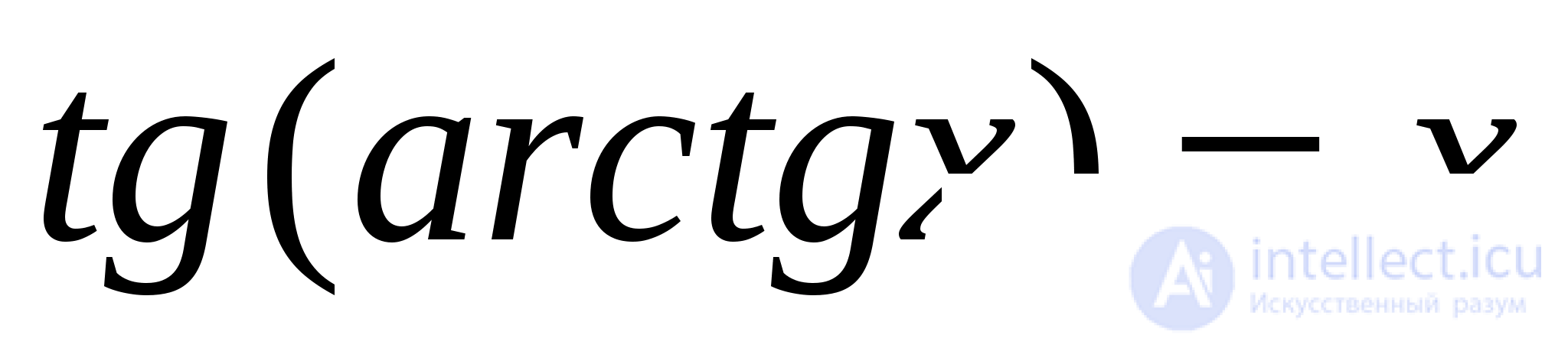


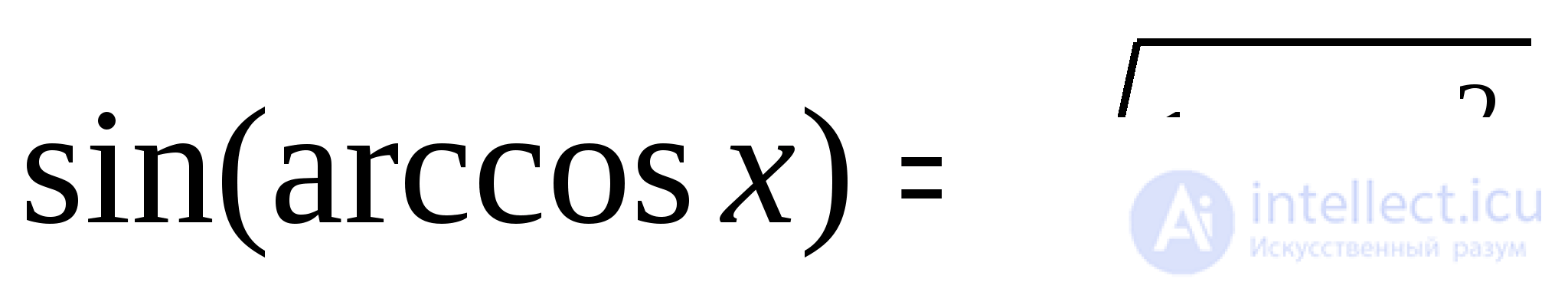
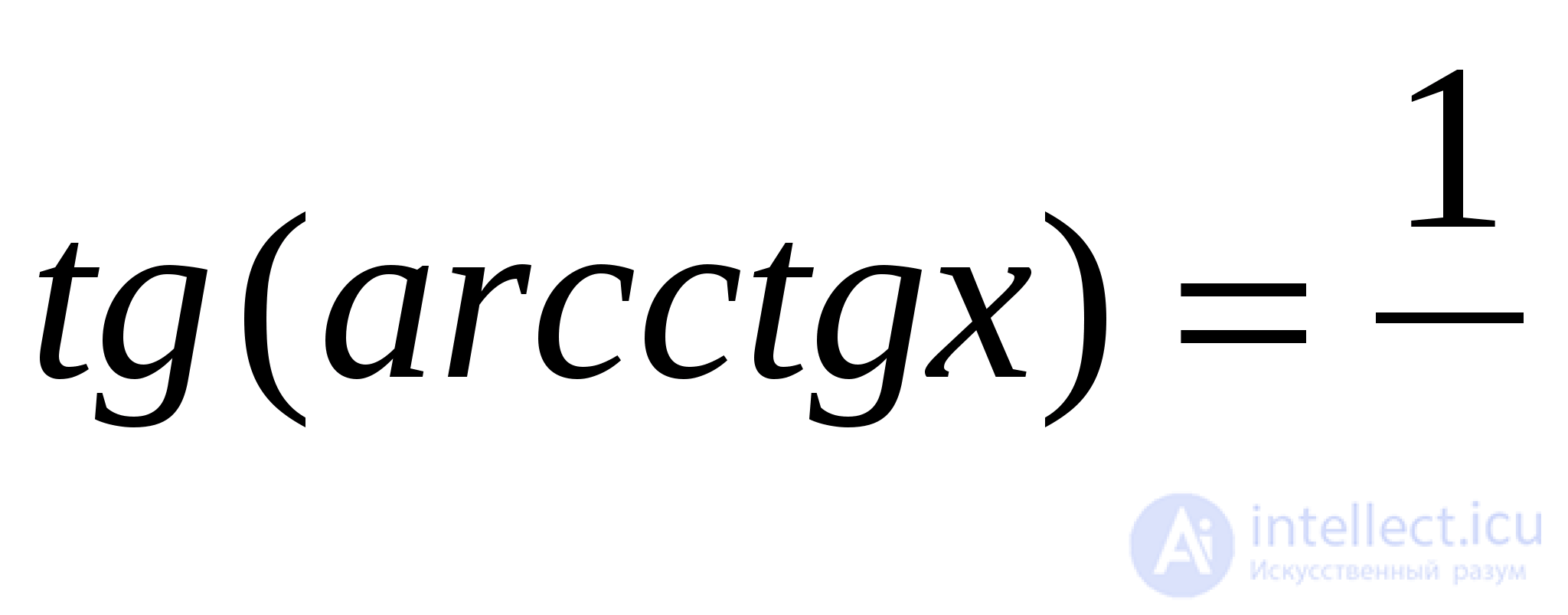 (13)
(13)

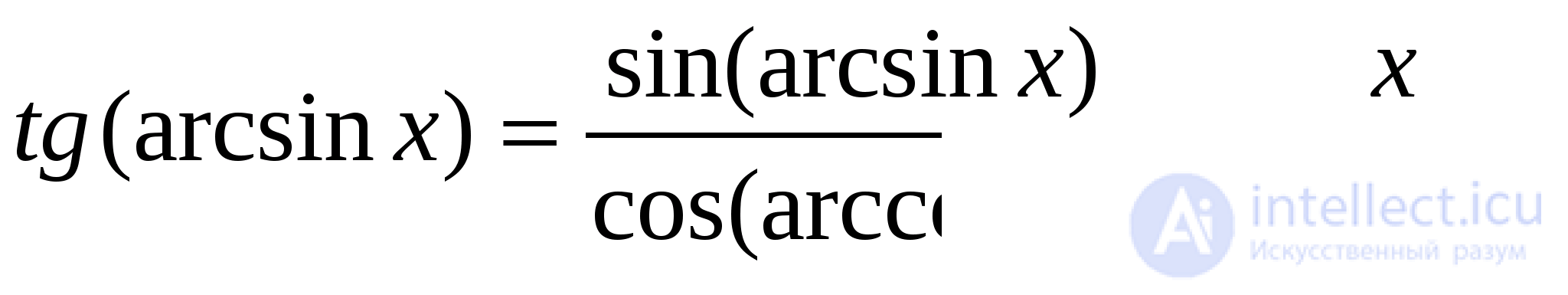
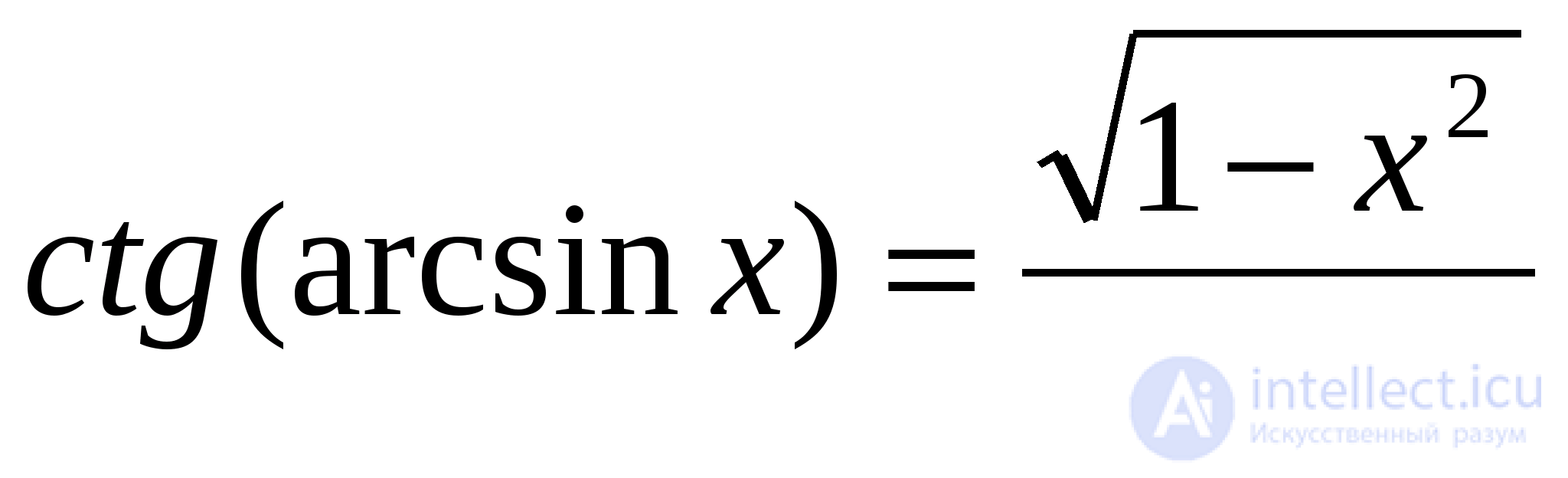
Формулы (13) легко выводятся из определений аркфункций и основных тригонометрических тождеств. Приведенные формулы можно дополнить подобными им формулами, полученными на основе двух тождеств
(14)
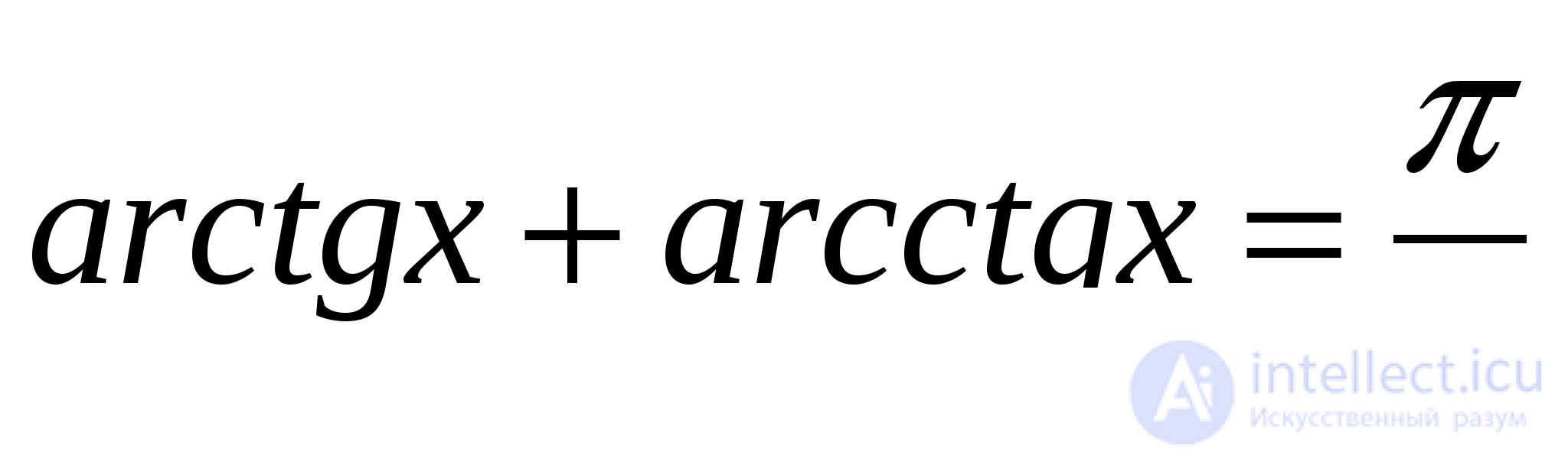
и формул приведения.
Основным недостатком упомянутых способов решения является нарушение равносильности уравнения в процессе его преобразования, вследствие чего можно ожидать появления “лишних” корней. Выявление лишних решений путем подстановки в исходное уравнение зачастую вызывает большие трудности либо а) из-за сложности вычислений не табличных значений аркфункций, либо б) в связи с тем, что полученное множество решений бесконечно.
Существует метод решения уравнения с аркфункциями, в процессе которого “лишние” корни вообще не возникают. Метод реализуется в трех приводимых ниже подходах, которые различаются в зависимости от числа аркфункций, участвующих в уравнении.
Подход(I): Исходное уравнение содержит две аркфункции. Разнесем их в разные части уравнения. Зададим двумя неравенствами области изменения левой и правой части уравнения. Ввиду монотонности аркфункций эти неравенства легко разрешаются относительно аргументов указанных функций. Решение последней системы неравенств и определяет тот промежуток, которому принадлежат корни исходного уравнения.
Задача 1. Решить уравнение

Решение: Для сравнения воспользуемся сначала традиционной схемой решения.
ОДЗ: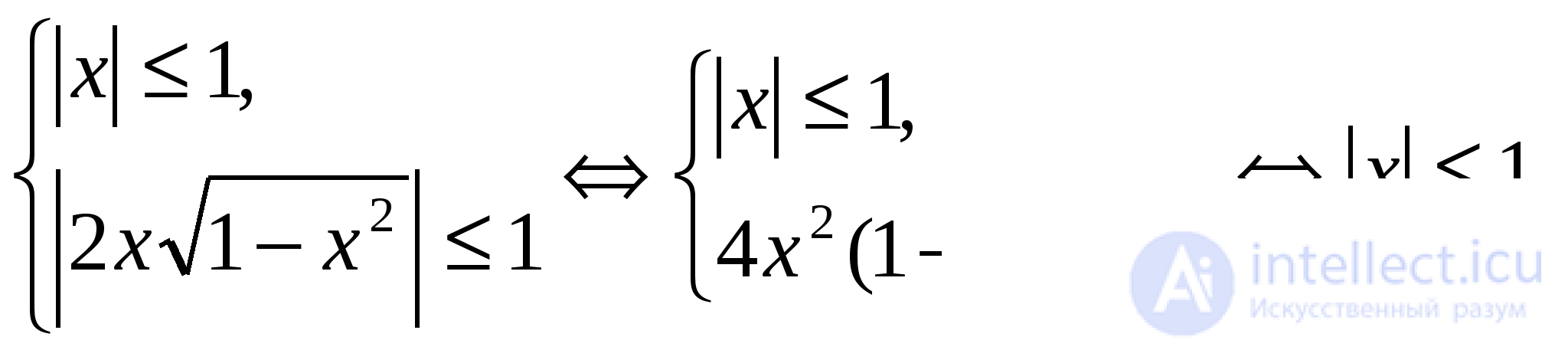
Далее,

С учетом ОДЗ, 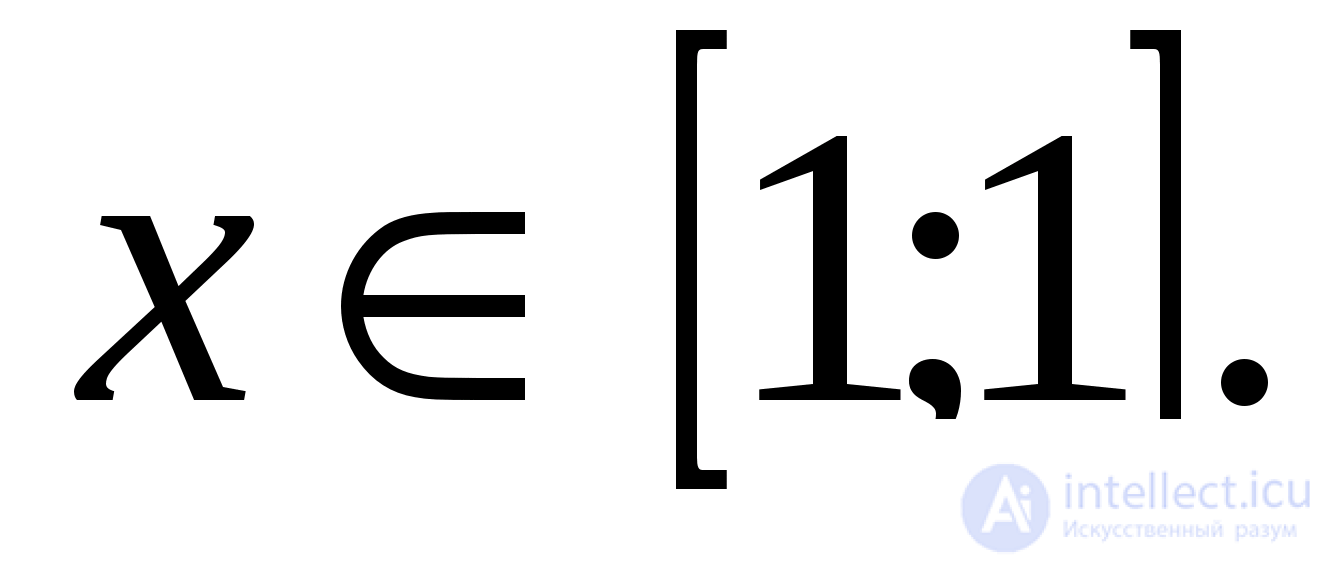
В полученном интервале содержится бесконечное множество “лишних” решений, удаление которых превращается здесь в отдельную задачу.
Альтернативное решение, использующее метод (I):
Положим 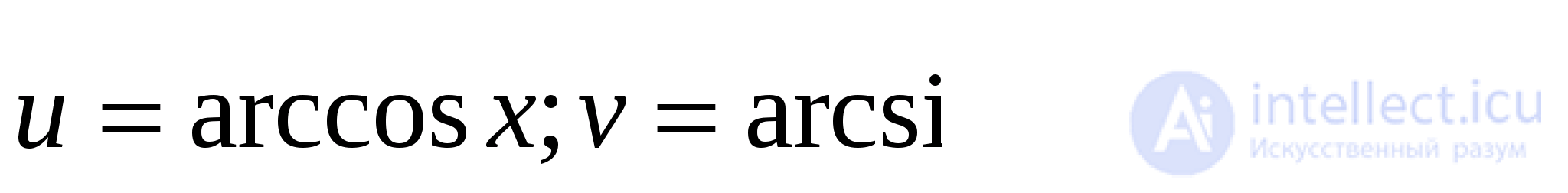 Так как
Так как  и
и  то исходное уравнение равносильно следующей системе:
то исходное уравнение равносильно следующей системе:
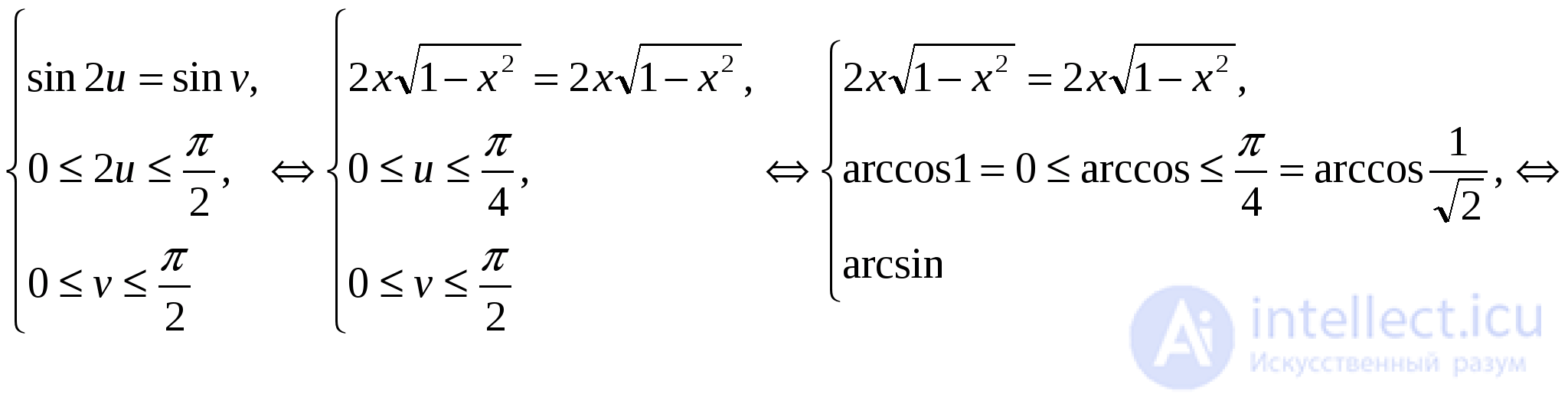
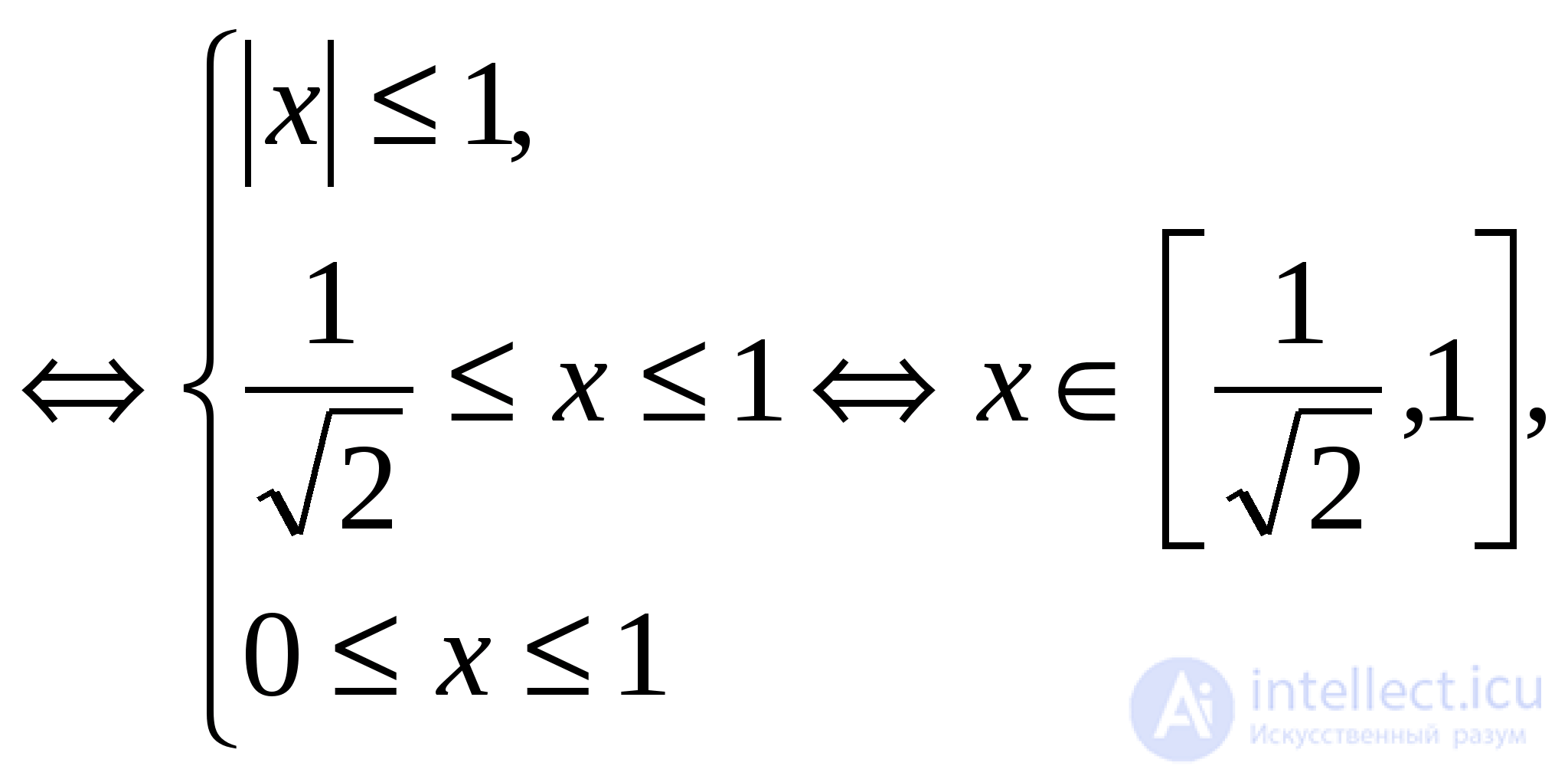
Ответ: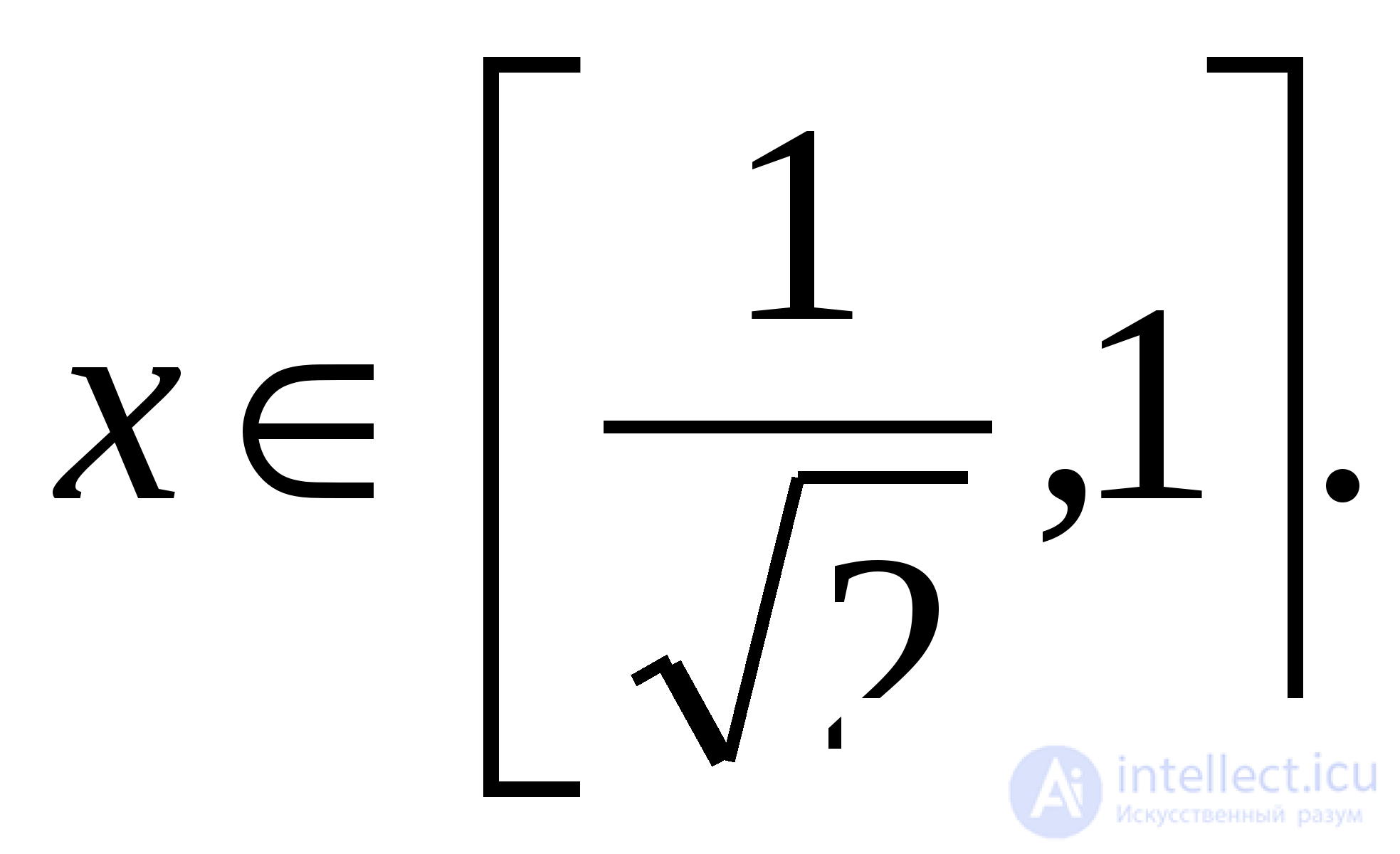
Задача 2. Решить уравнение
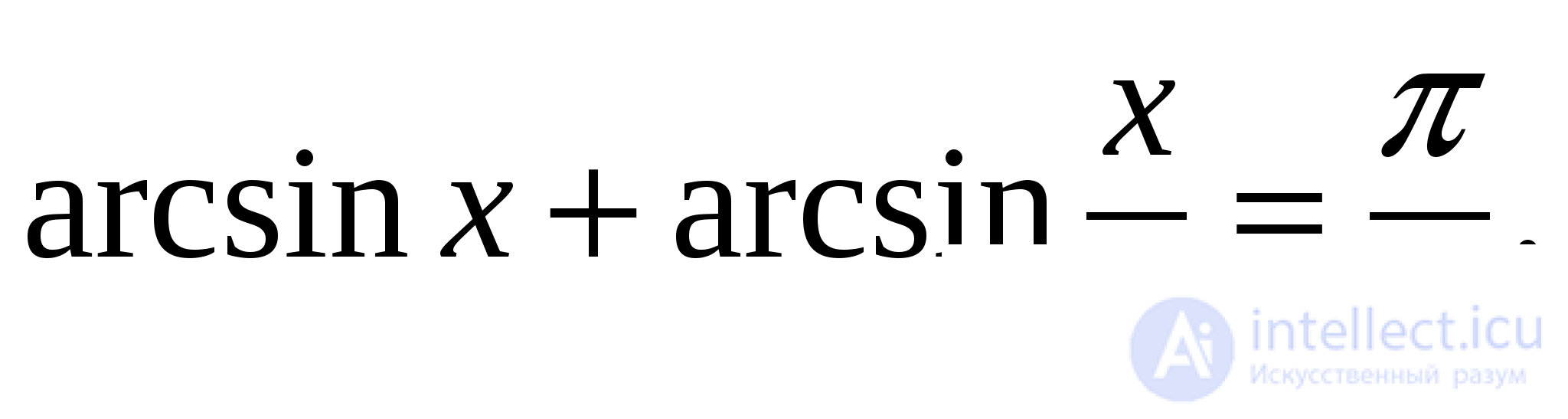
Решение: Положим  Перепишем уравнение в виде:
Перепишем уравнение в виде:
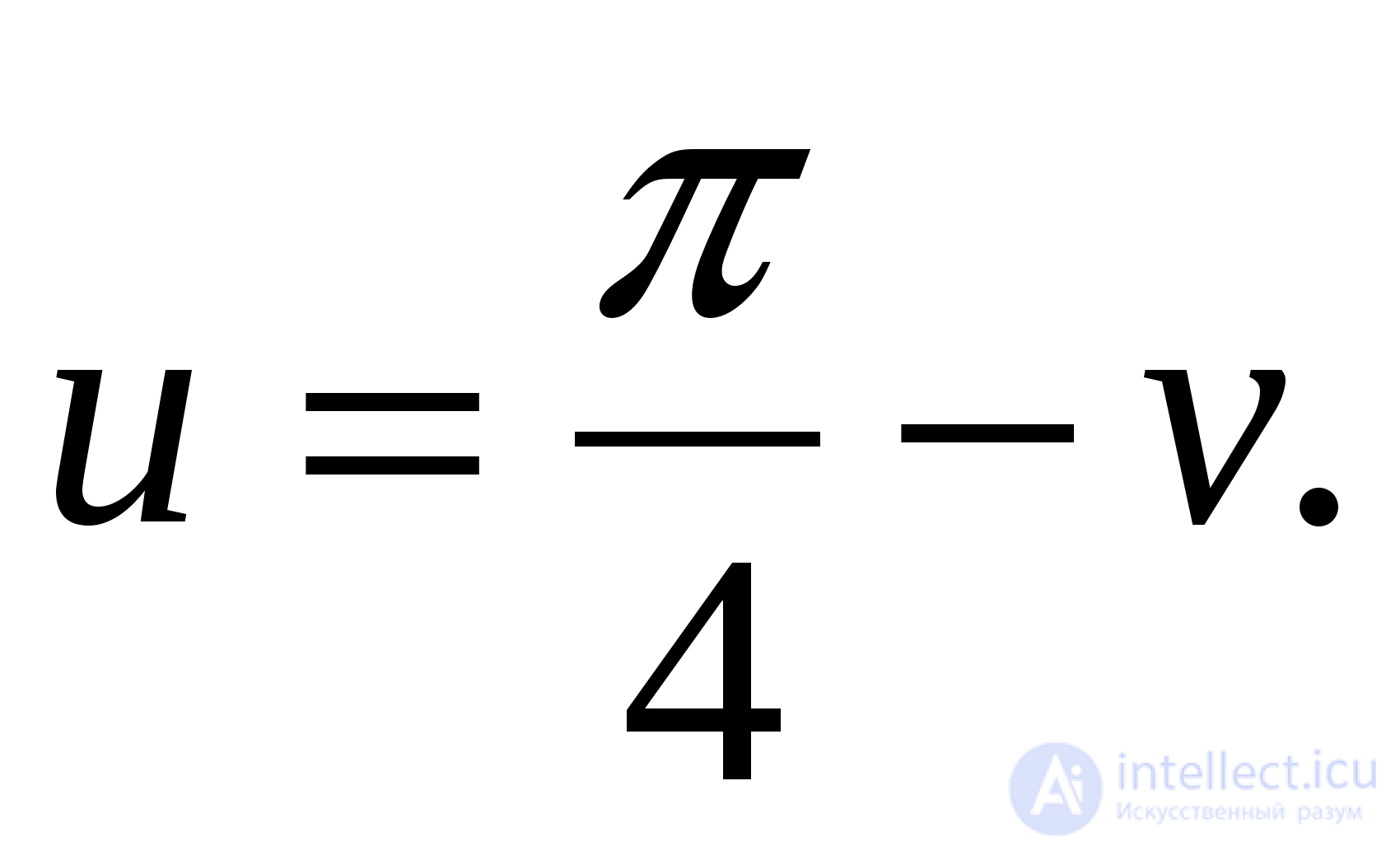
Так как 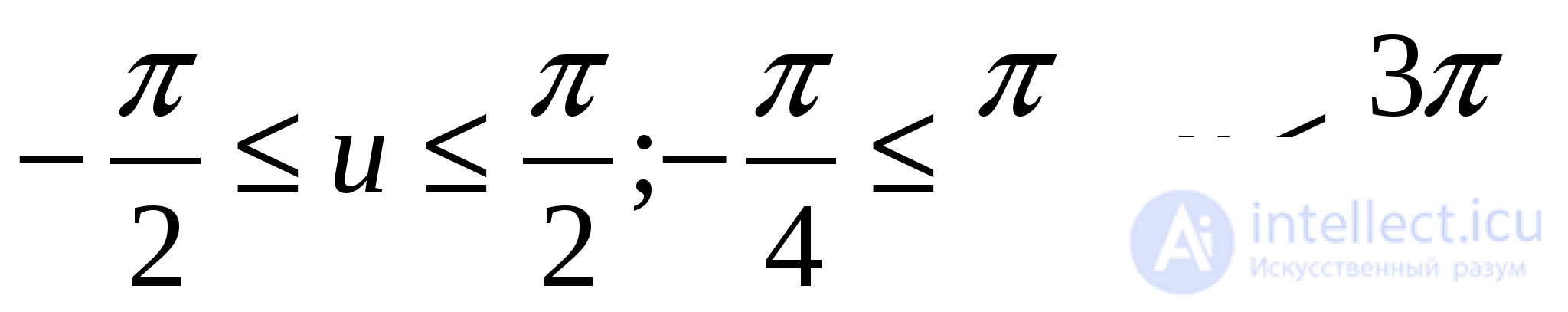 то исходное уравнение равносильно системе:
то исходное уравнение равносильно системе:

Задача 3. Решить уравнение

Решение: Обозначим
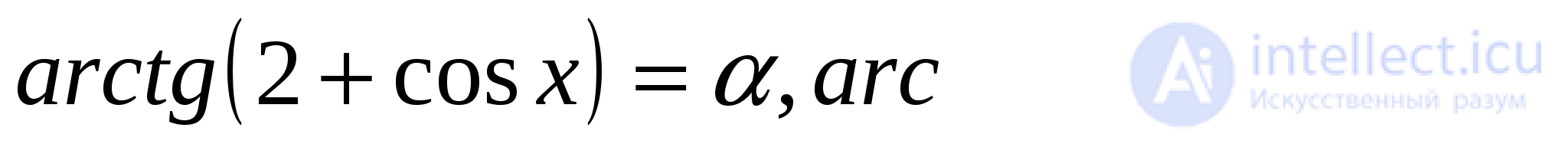
Так как и 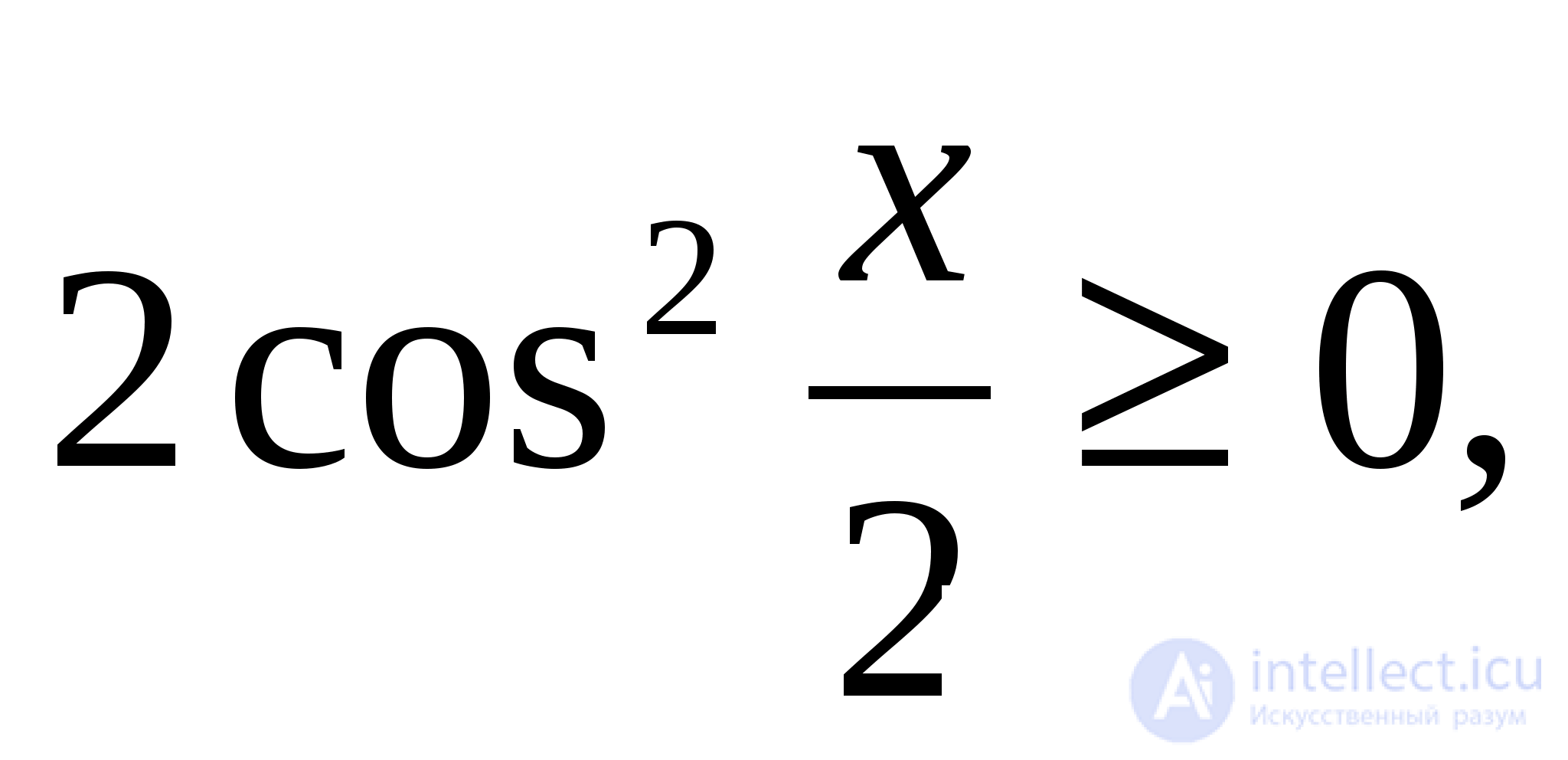 то
то  и
и 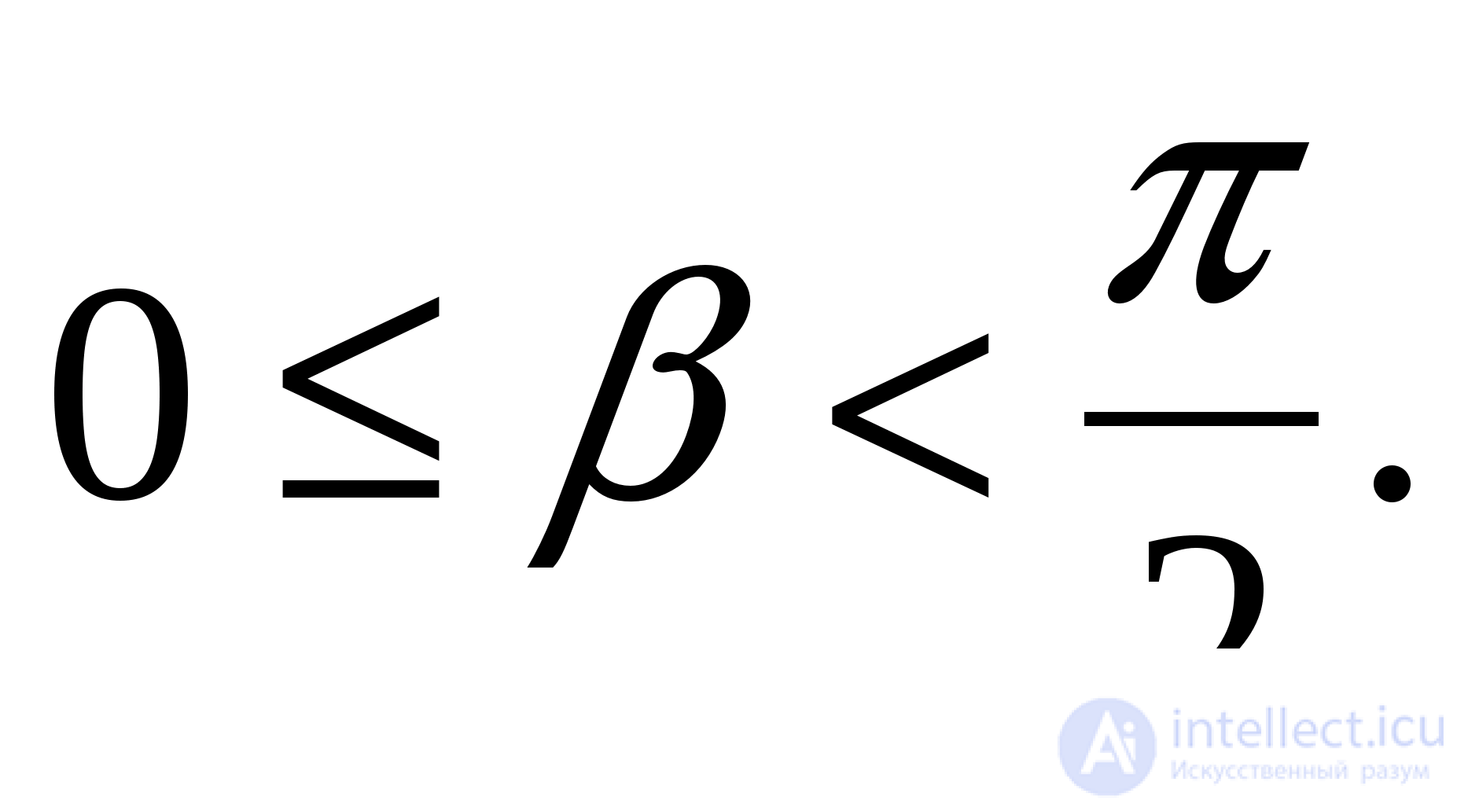
Уравнение принимает вид 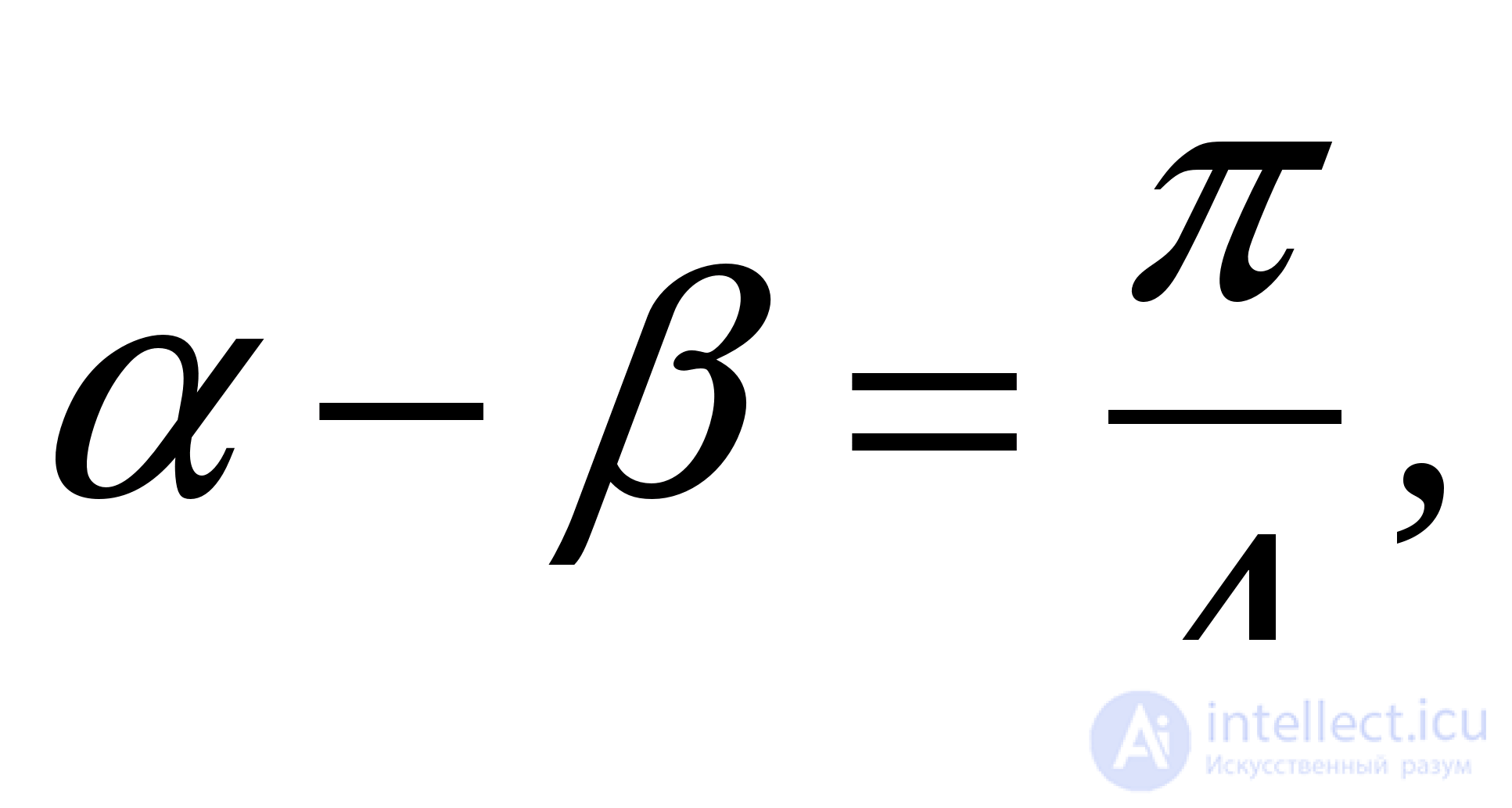 причем
причем
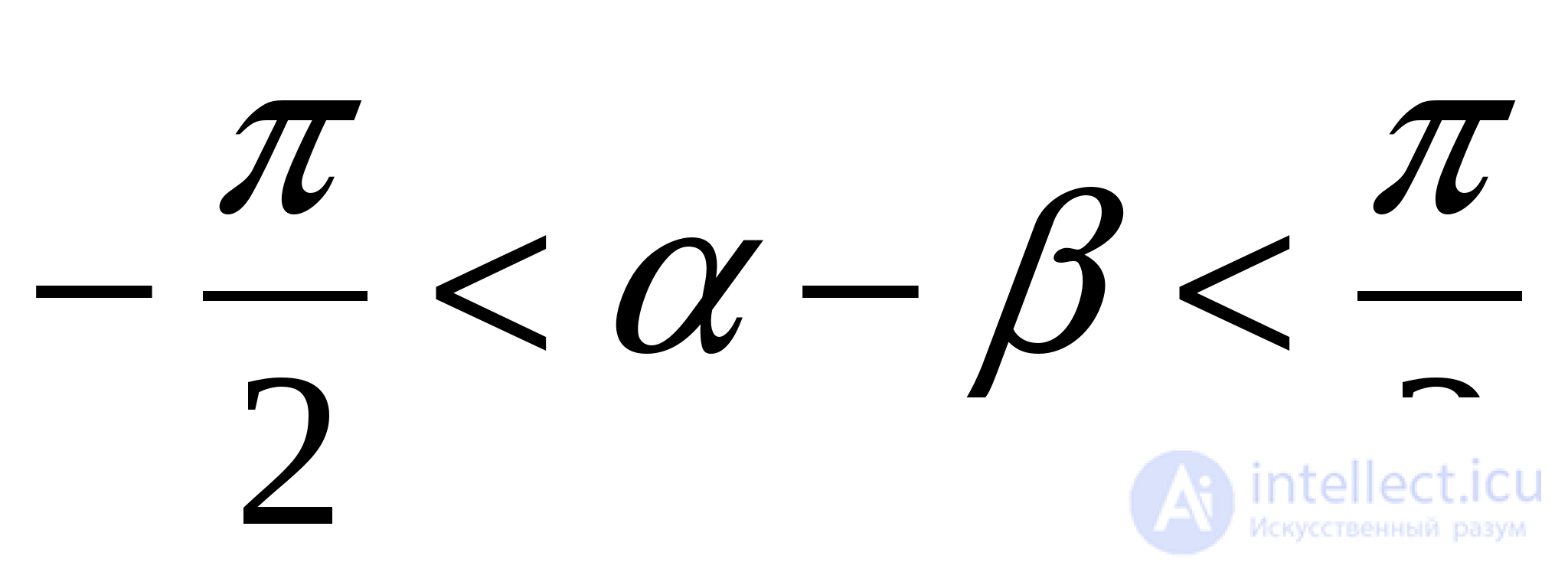 и
и
Так как  - интервал монотонности тангенса, то уравнение равносильно уравнению
- интервал монотонности тангенса, то уравнение равносильно уравнению 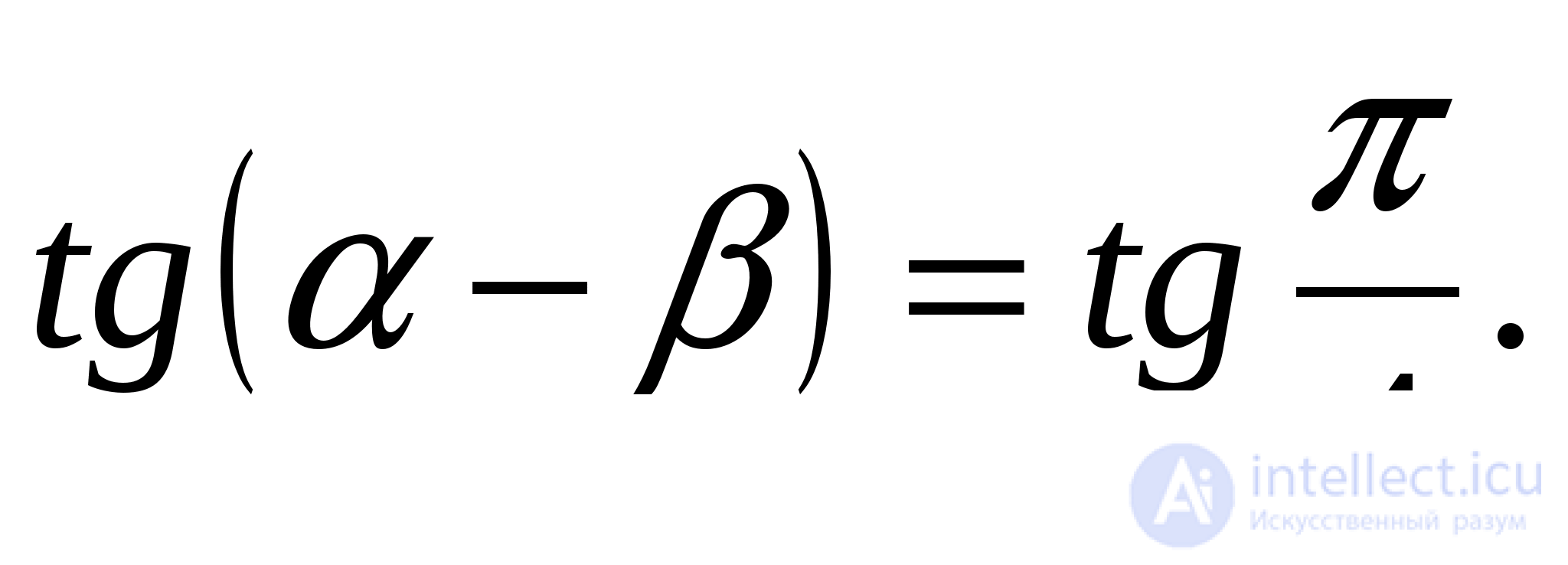
Переходя к уравнению
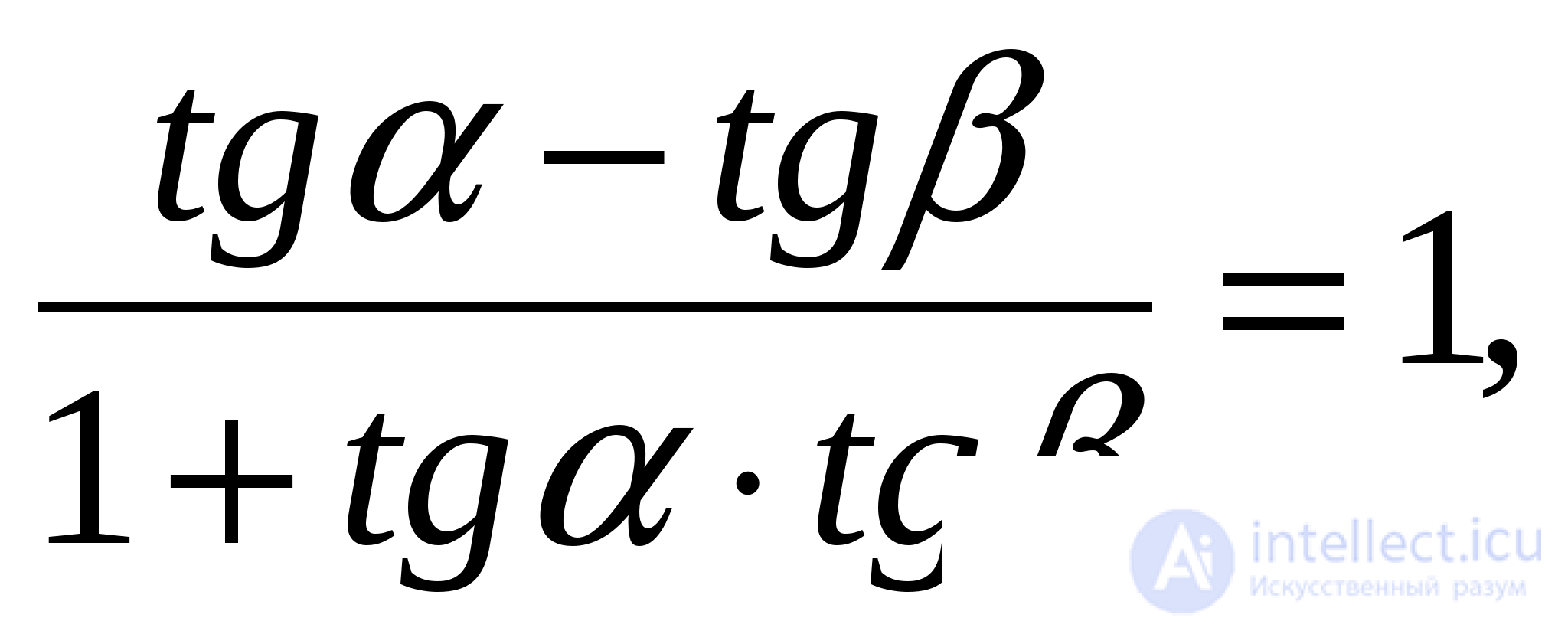
можно потерять те корни, для которых 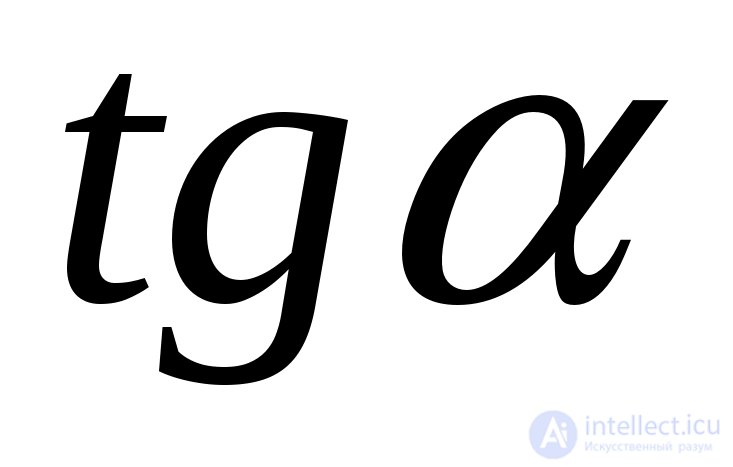 и
и 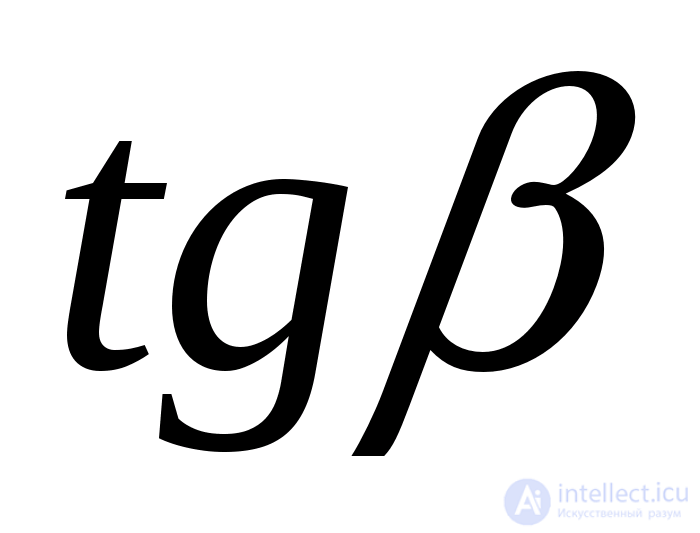 не существует. В данном случае этого не произойдет, поскольку
не существует. В данном случае этого не произойдет, поскольку
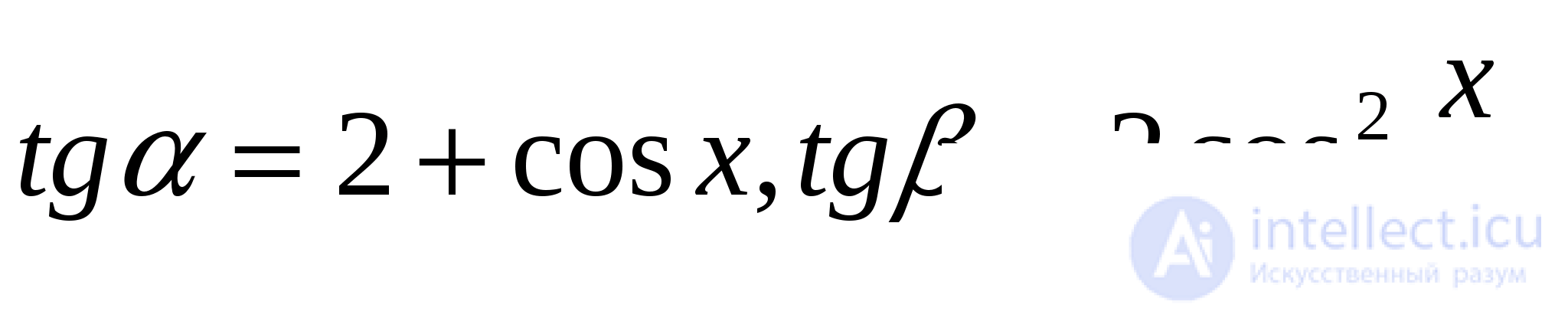
А правые части существуют всегда. Получаем уравнение
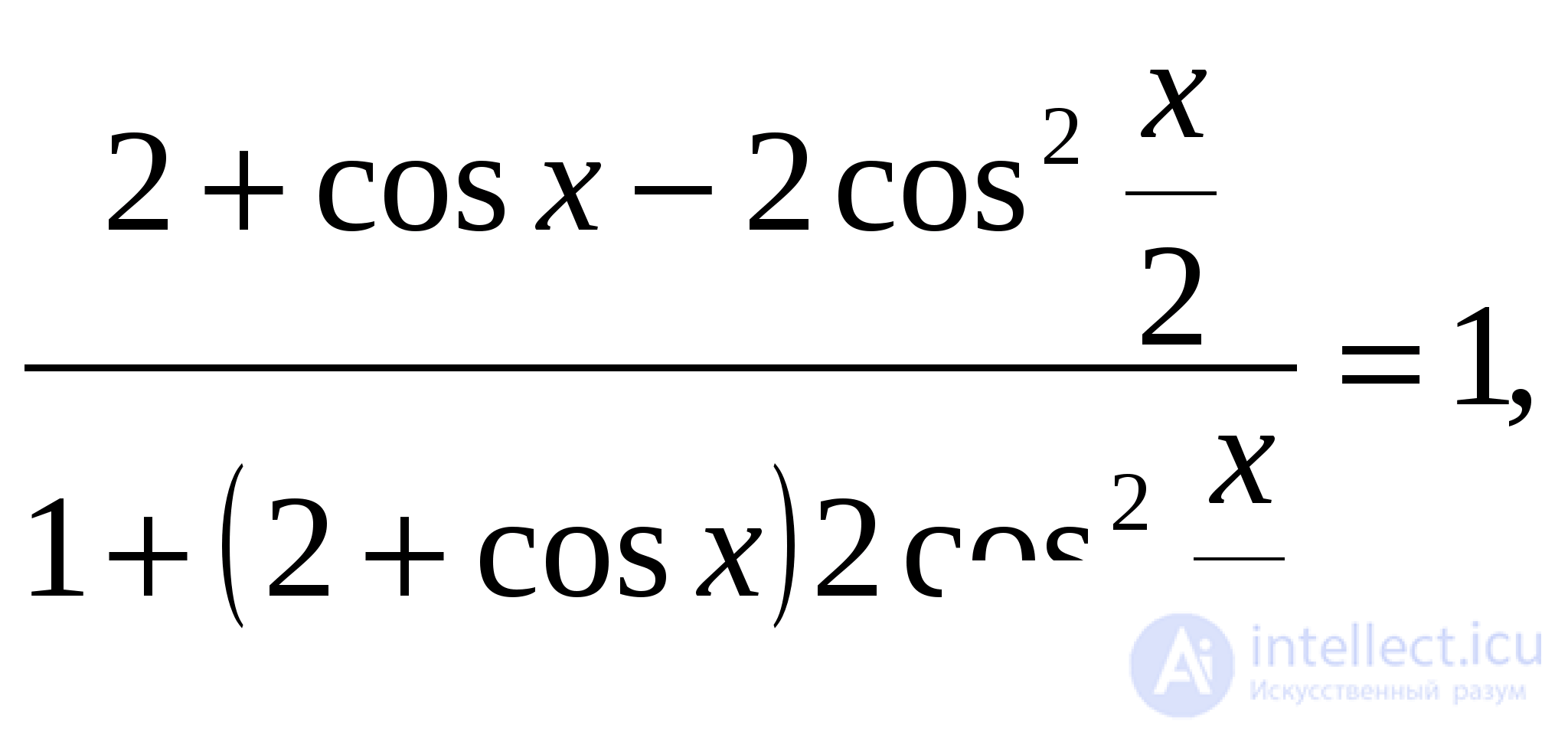
которое после преобразований принимает вид
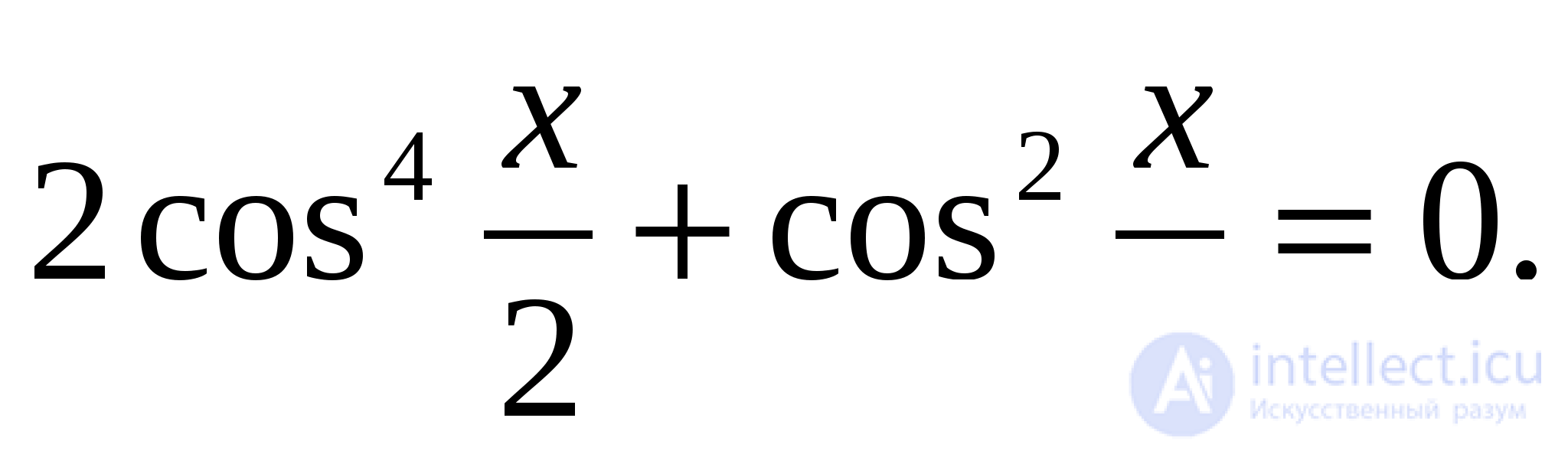
Так как уравнение  не имеет решений, то остается
не имеет решений, то остается 
Ответ: 
Подход (II): Пусть исходное уравнение содержит более двух аркфункций. В этом случае равносильность преобразований сохраняется при использовании следующих схем решения:
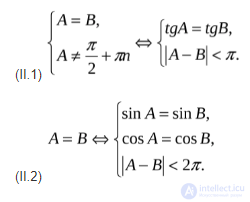
При решении задач проверка неравенств 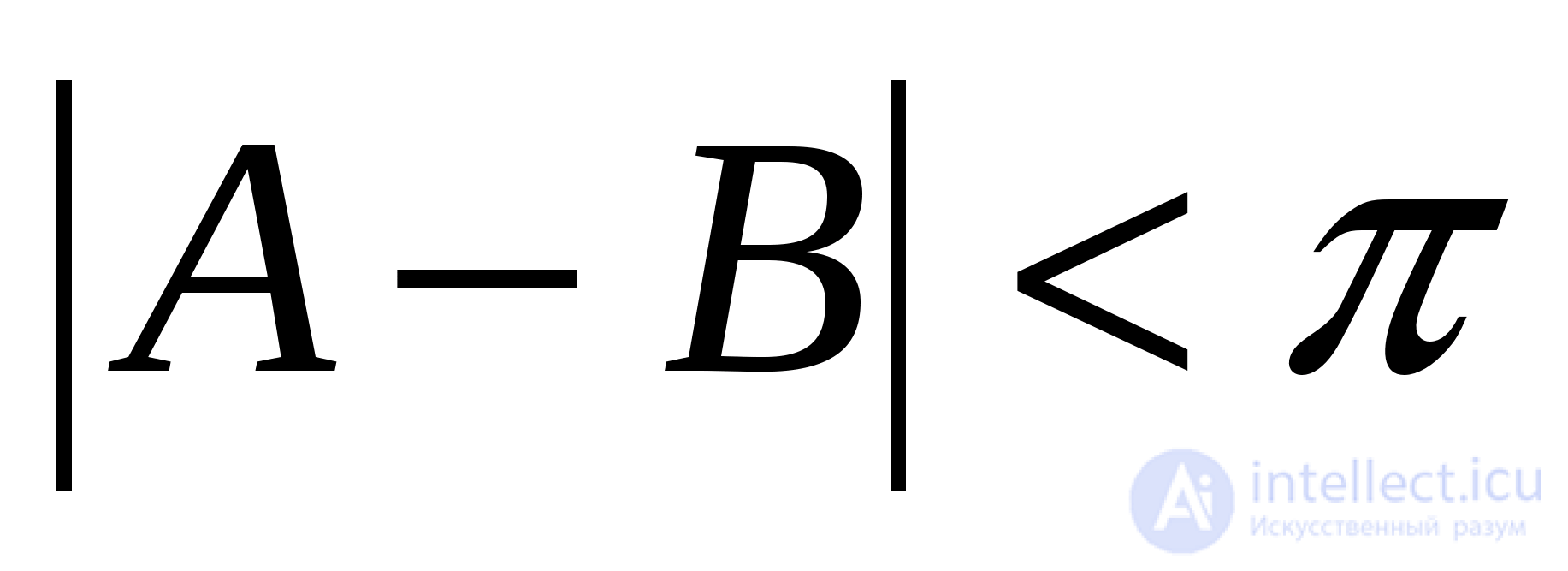 или
или 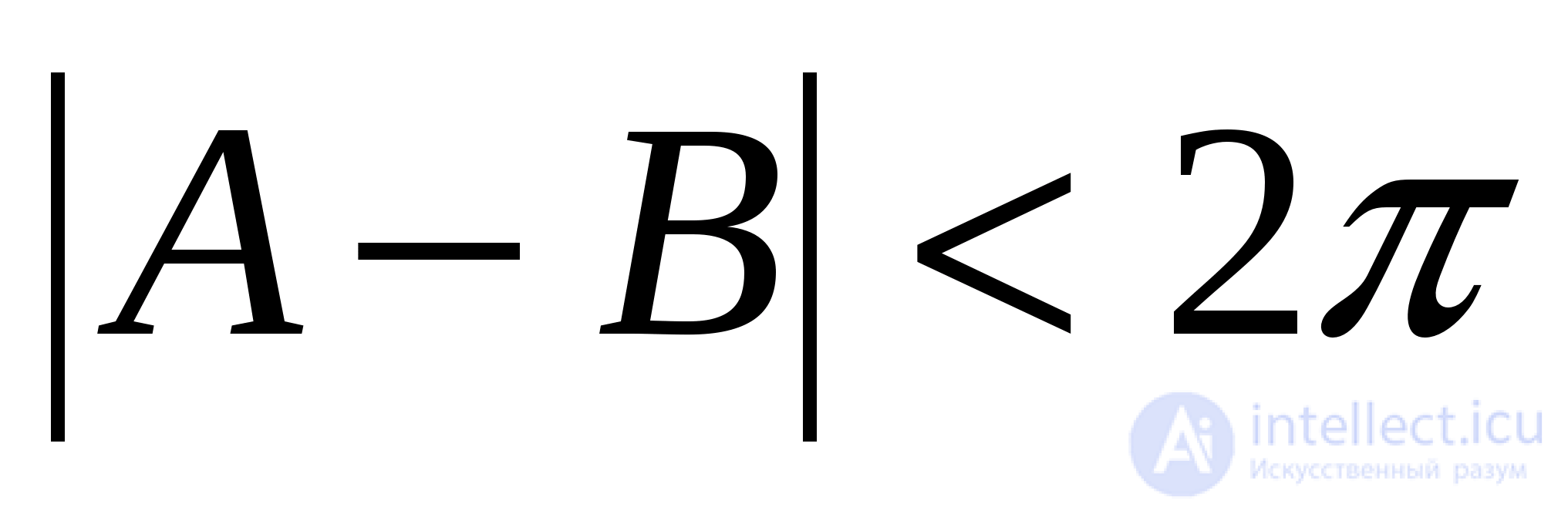 не вызывает сложностей и сводится к сопоставлению областей изменения входящих в уравнение аркфункций.
не вызывает сложностей и сводится к сопоставлению областей изменения входящих в уравнение аркфункций.
Задача 4. Решить уравнение: 
Решение: Положим 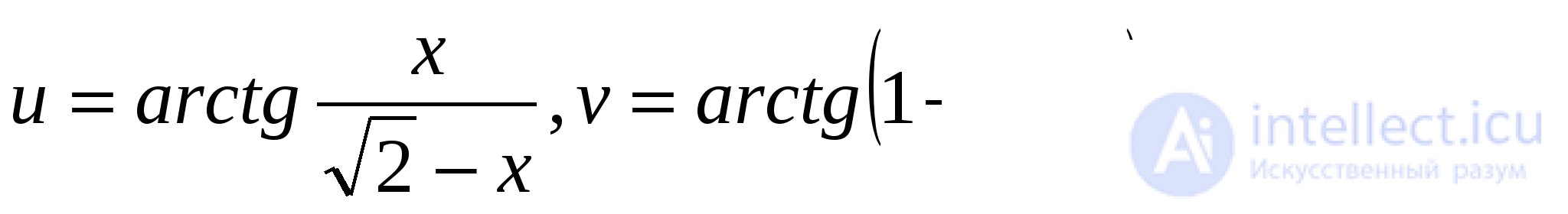 Исходное уравнение равносильно системе:
Исходное уравнение равносильно системе:
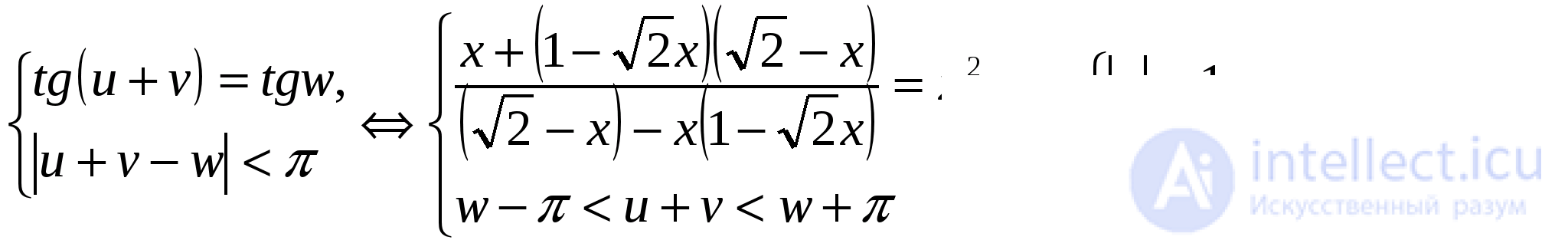
Так как  то достаточно убедиться, что
то достаточно убедиться, что 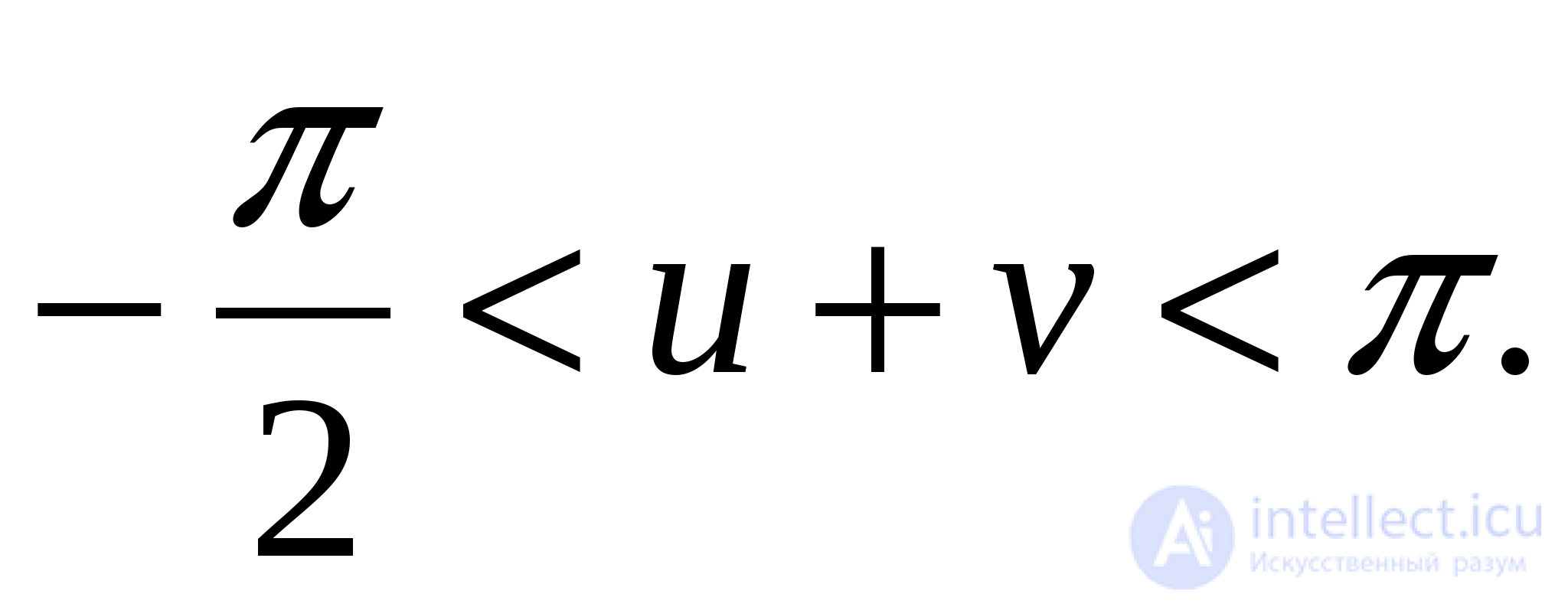
Правое неравенство верно в силу границ изменения арктангенса. Левая часть неравенства следует из того, что  при
при 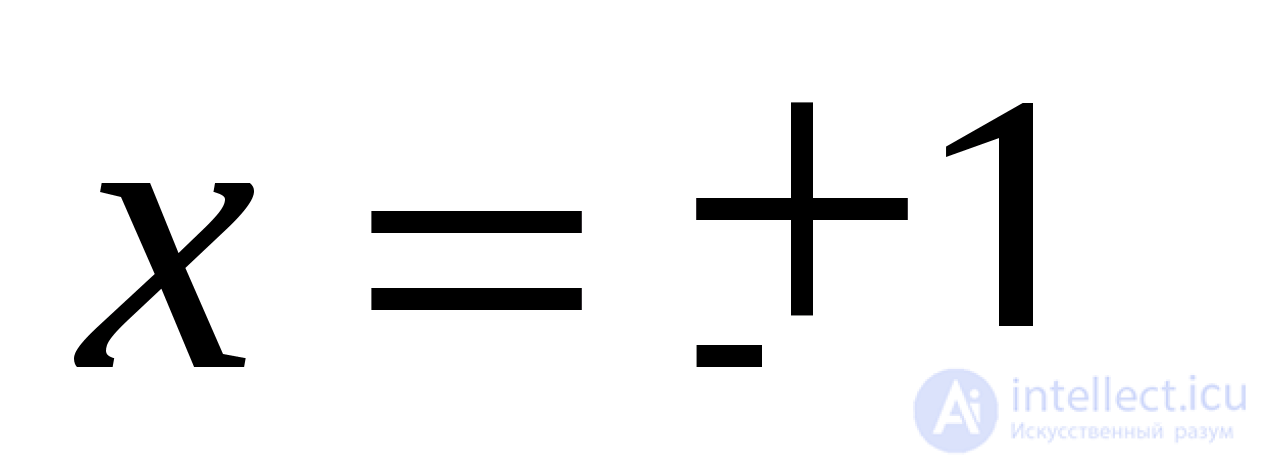
Ответ: 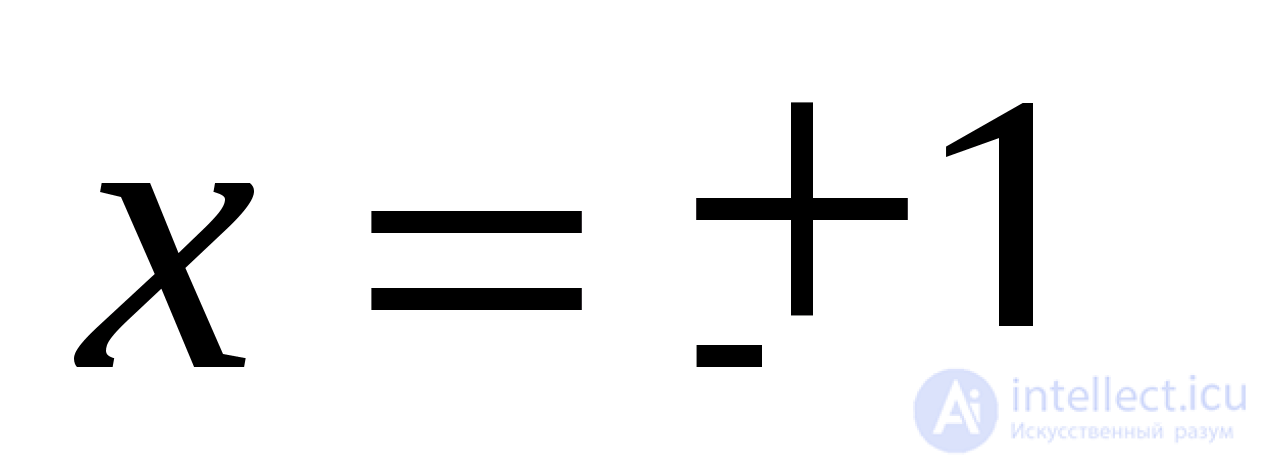
Задача 5. Решить уравнение: 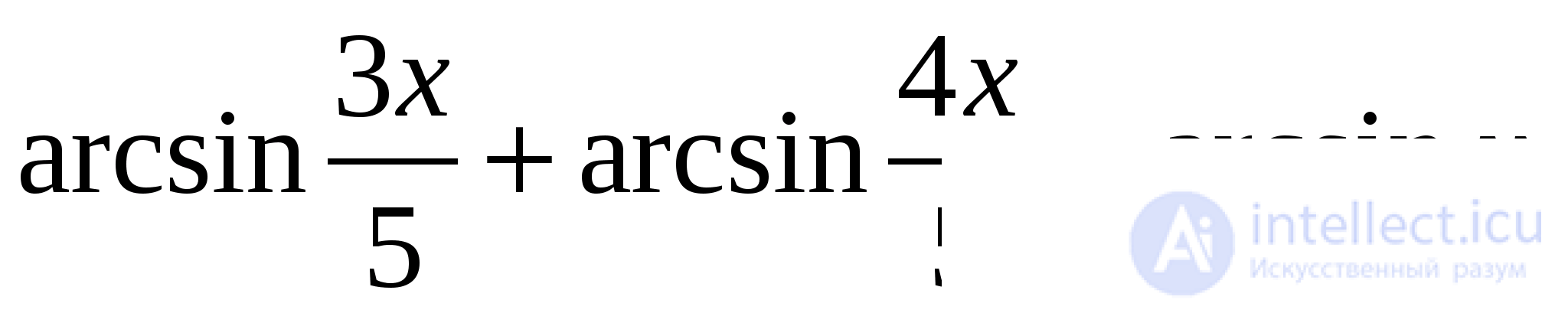
Решение: Положим  Тогда исходное уравнение равносильно системе:
Тогда исходное уравнение равносильно системе:
(*)
Последнее неравенство с очевидностью следует из неравенств  задающих промежутки изменения переменных. Поэтому система (*) равносильна следующей системе:
задающих промежутки изменения переменных. Поэтому система (*) равносильна следующей системе: 
Корень первого уравнения системы 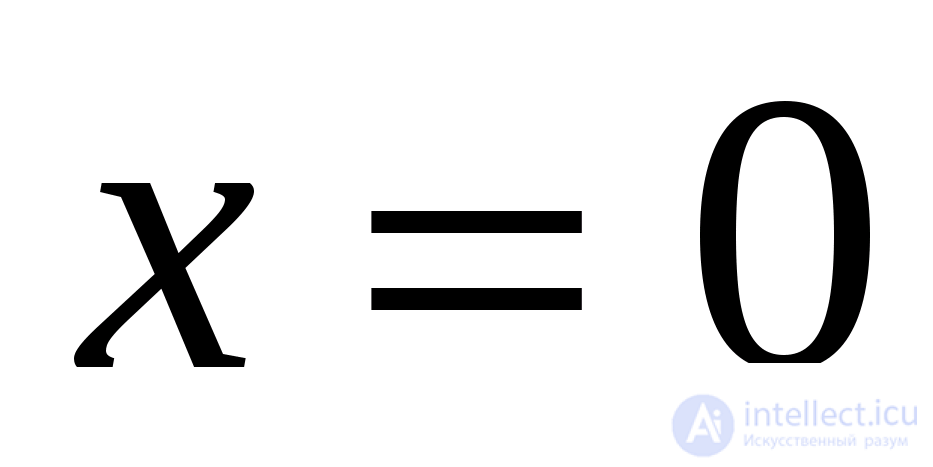 является решением исходного уравнения. После сокращения первого уравнения на
является решением исходного уравнения. После сокращения первого уравнения на 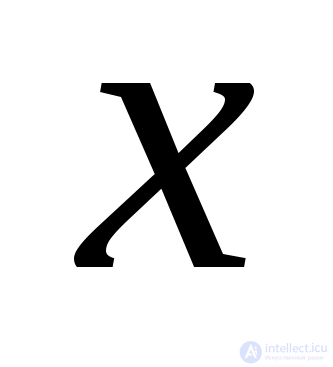 возводим его в квадрат.
возводим его в квадрат.

Задача 6. Решить уравнение 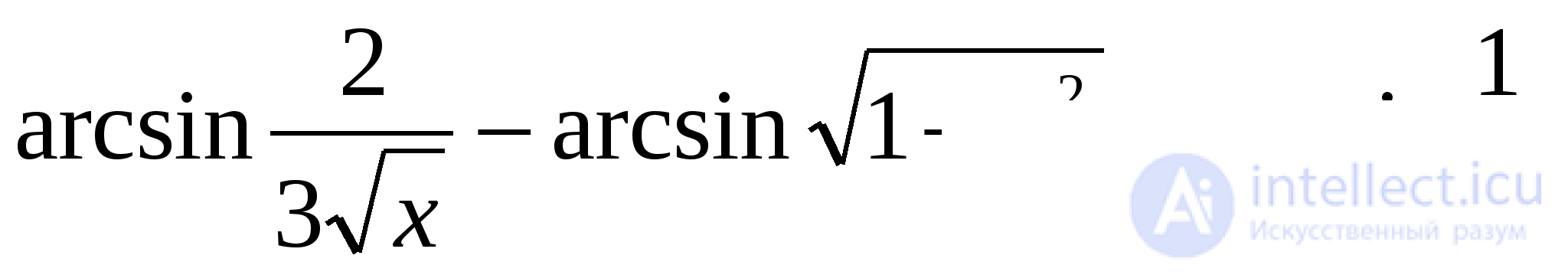
Решение: Пусть

Так как 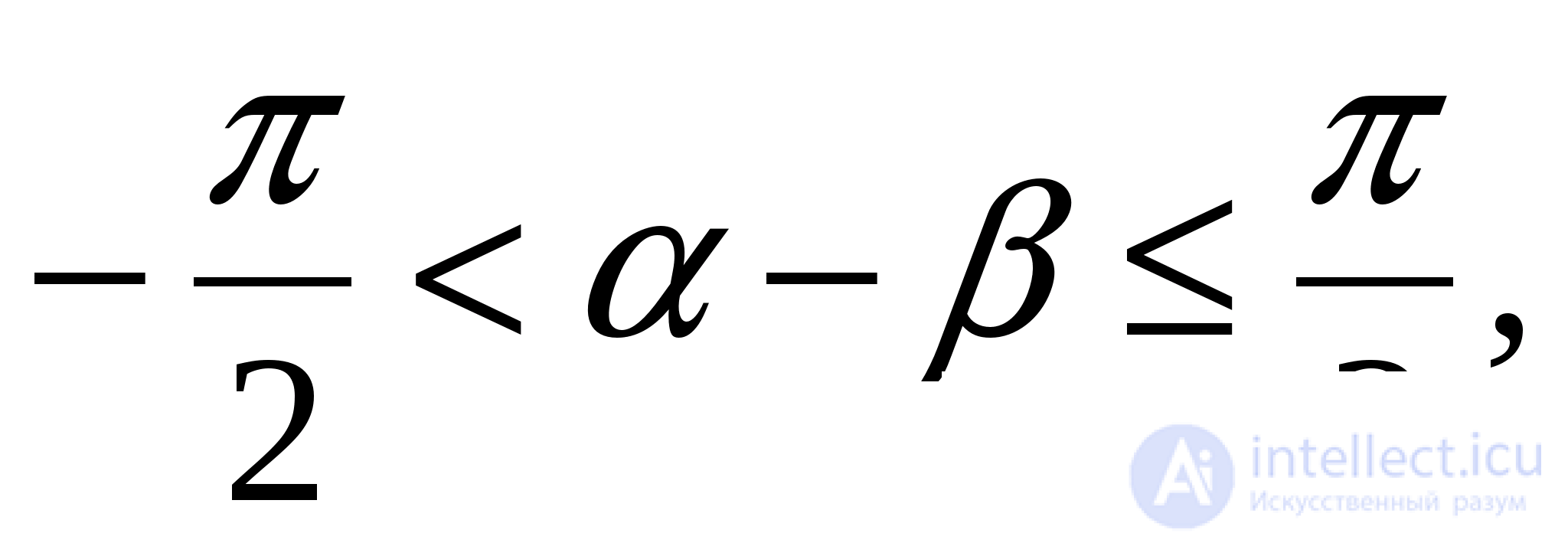 то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:
то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:
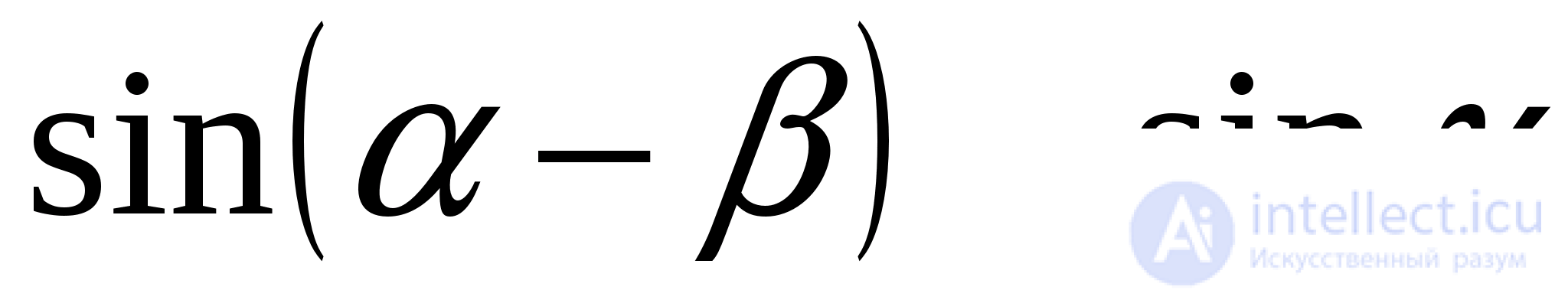
или

После упрощений получим уравнение
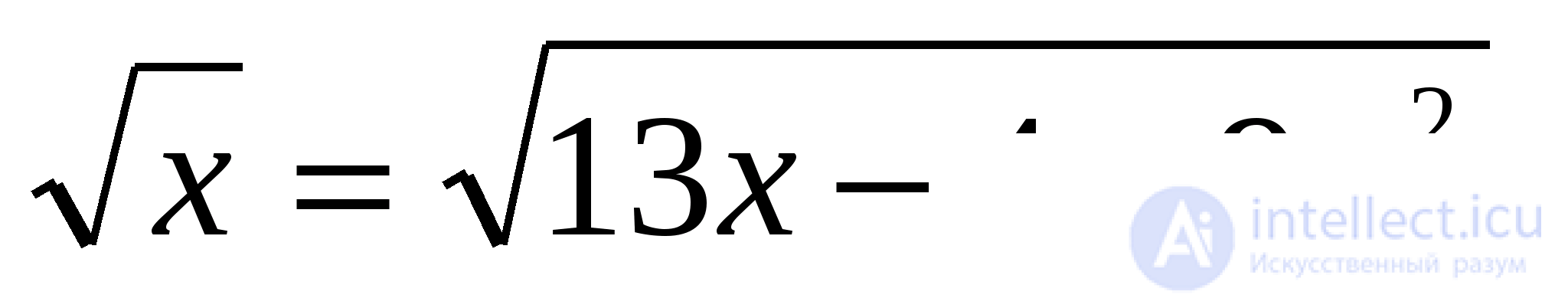
имеющее единственный корень 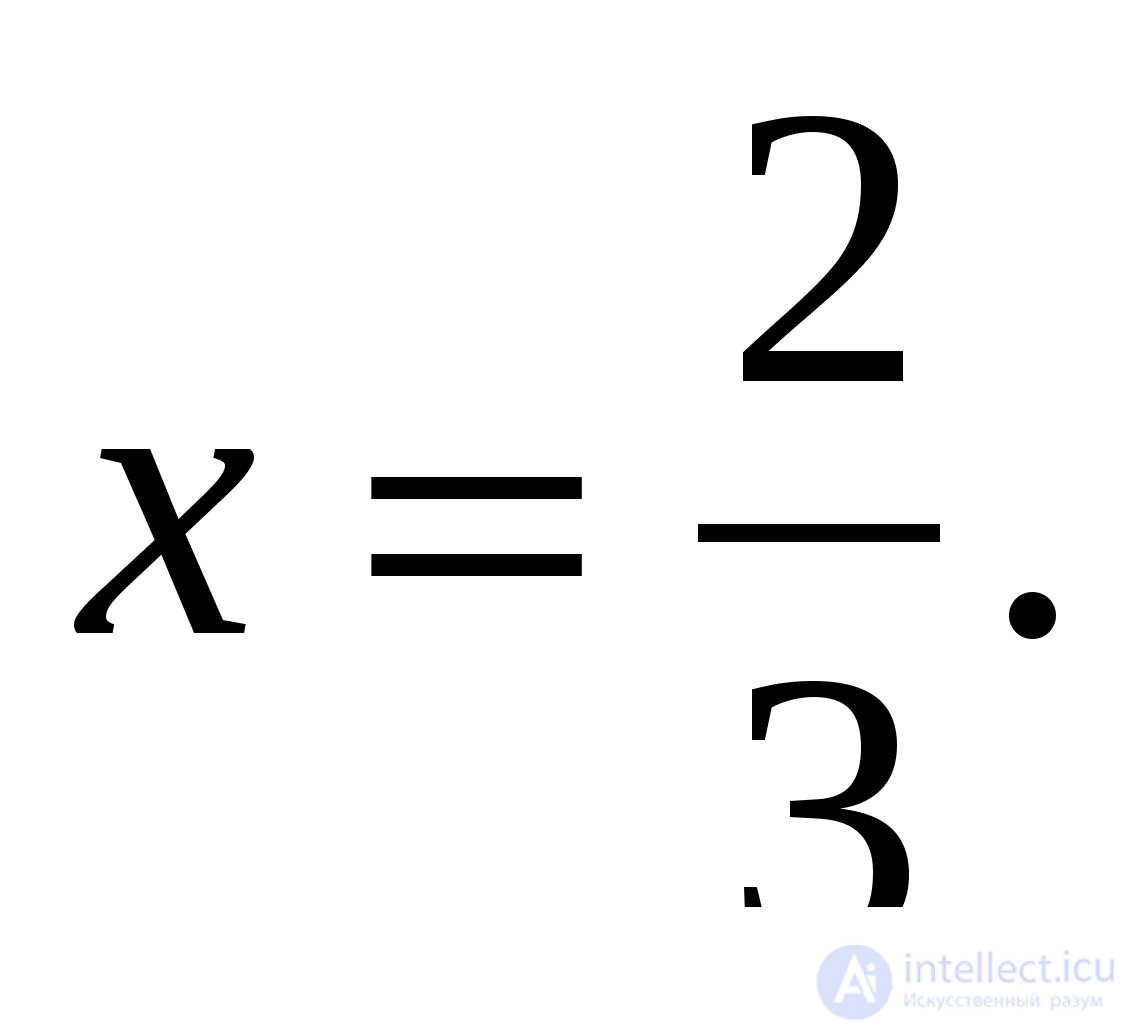 Делаем проверку и убеждаемся, что
Делаем проверку и убеждаемся, что 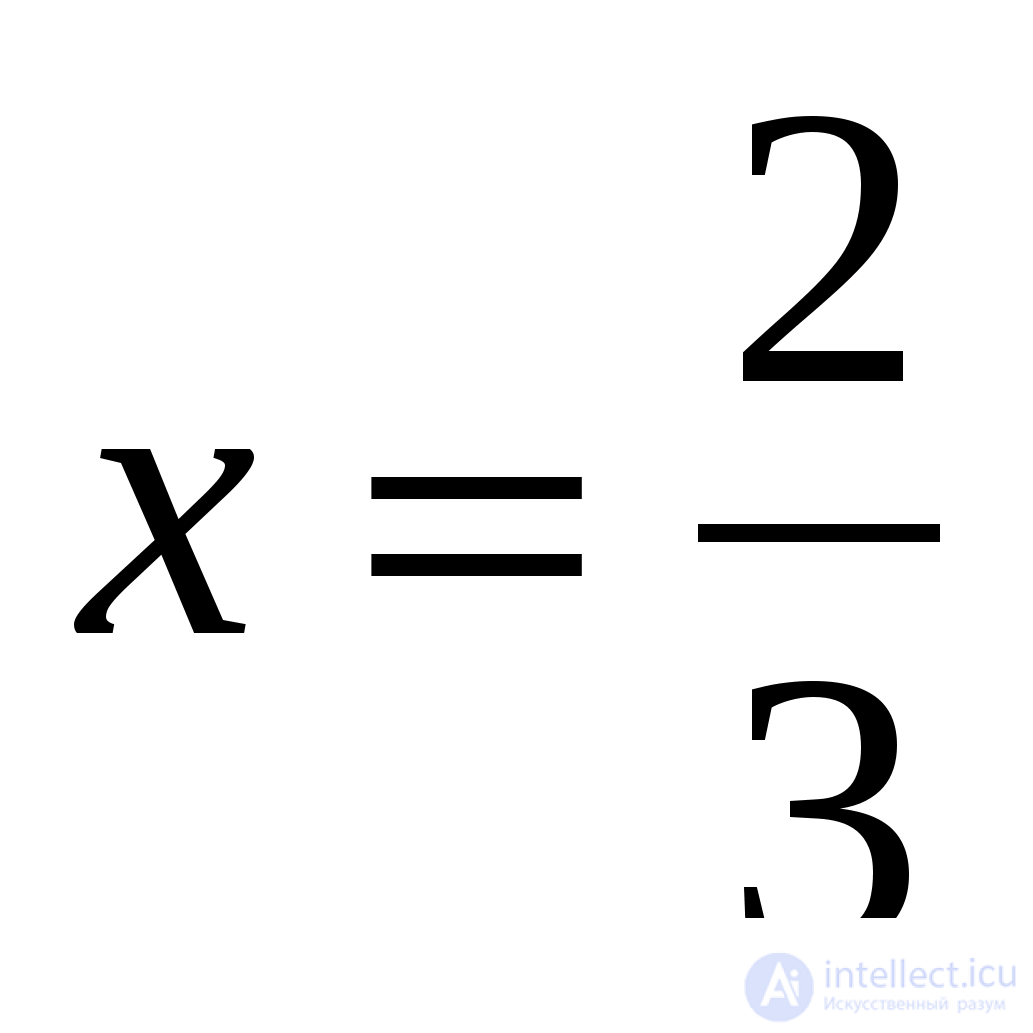 является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.
является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.
Ответ: 
Задача 7. Решить уравнение
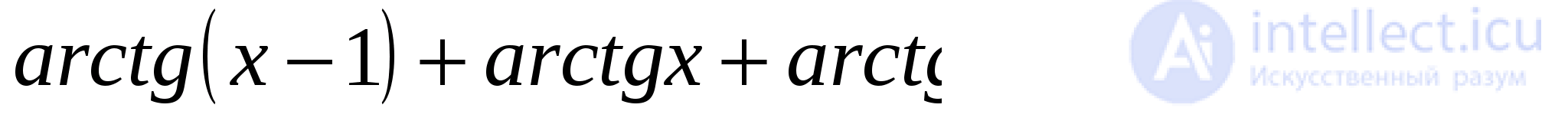
Решение: Введем обозначения
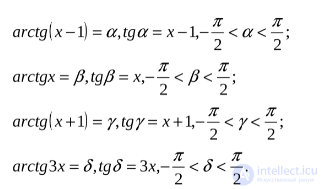
Данное уравнение принимает вид или  Обе части уравнения лежат в интервале Если взять котангенсы от обеих частей уравнения, то можно потерять лишь корень, которому соответствует значение углов, равное 0, так как это – единственное значение из интервала
Обе части уравнения лежат в интервале Если взять котангенсы от обеих частей уравнения, то можно потерять лишь корень, которому соответствует значение углов, равное 0, так как это – единственное значение из интервала 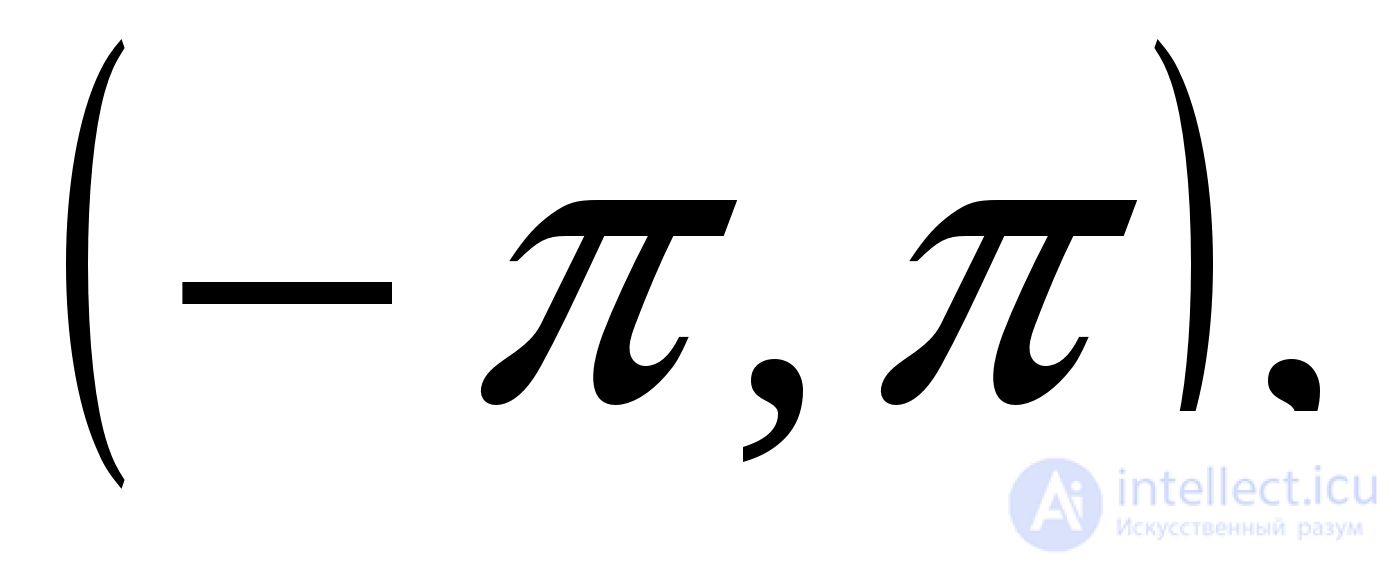 в котором котангенс не существует. Проверим, будет ли выполняться равенство
в котором котангенс не существует. Проверим, будет ли выполняться равенство 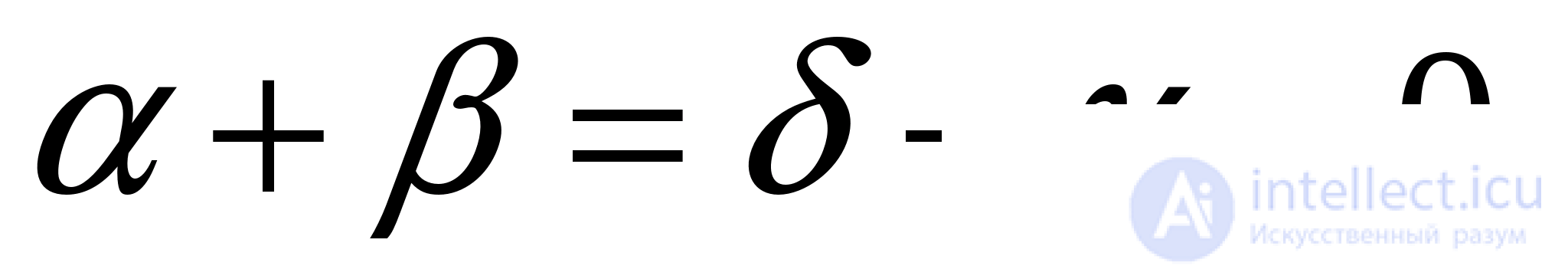 Если
Если  то
то 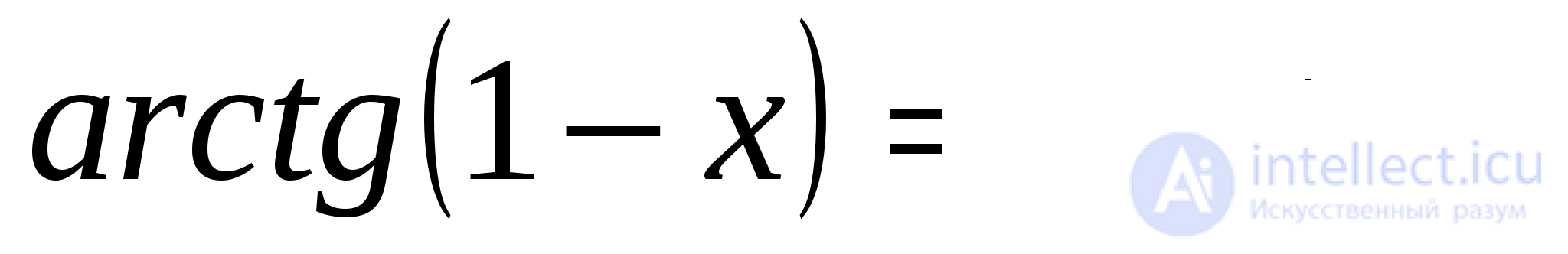 откуда
откуда 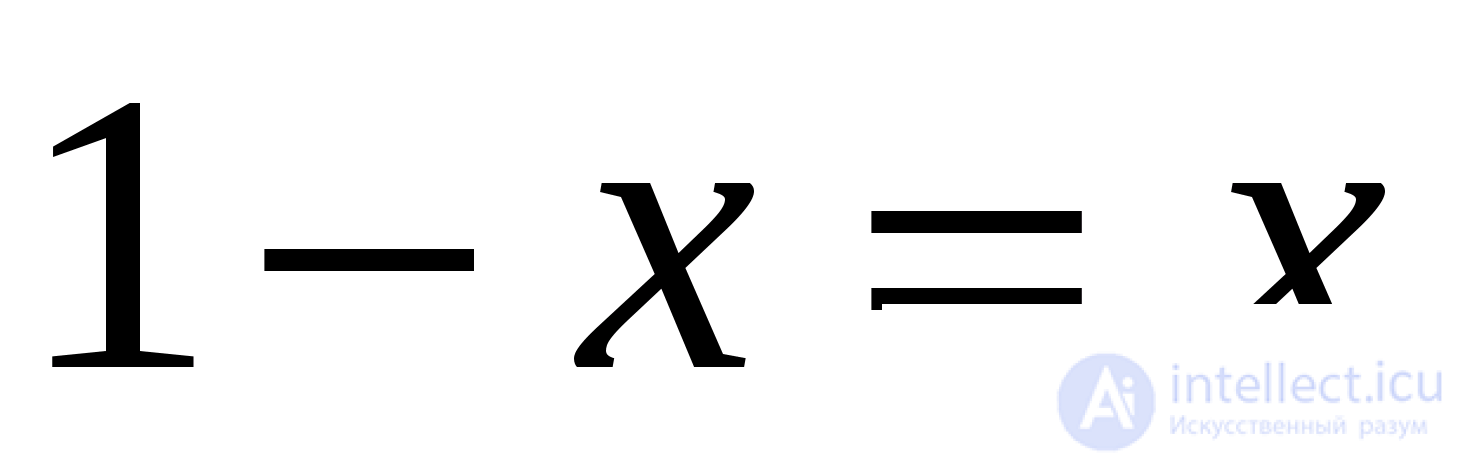 и
и 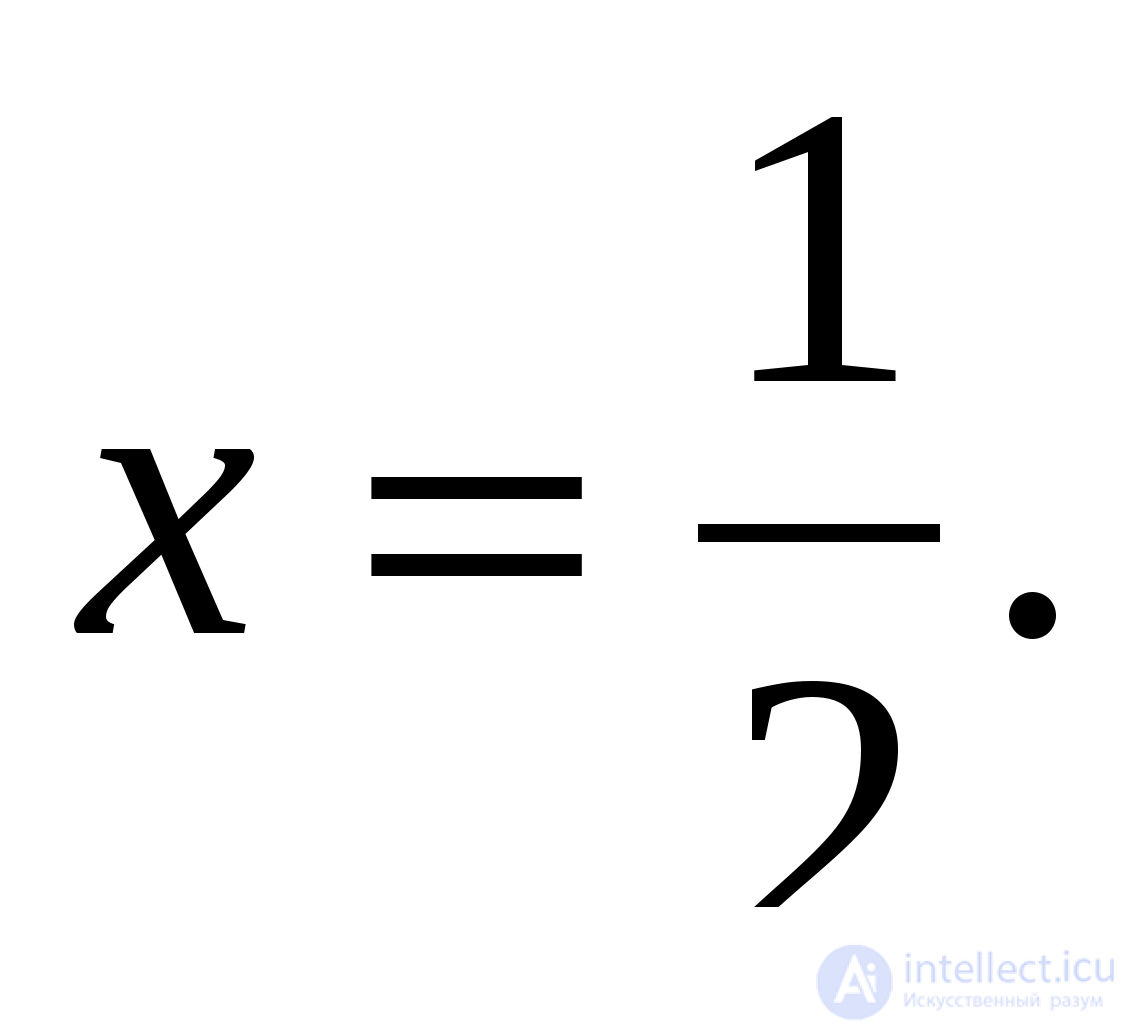 При
При 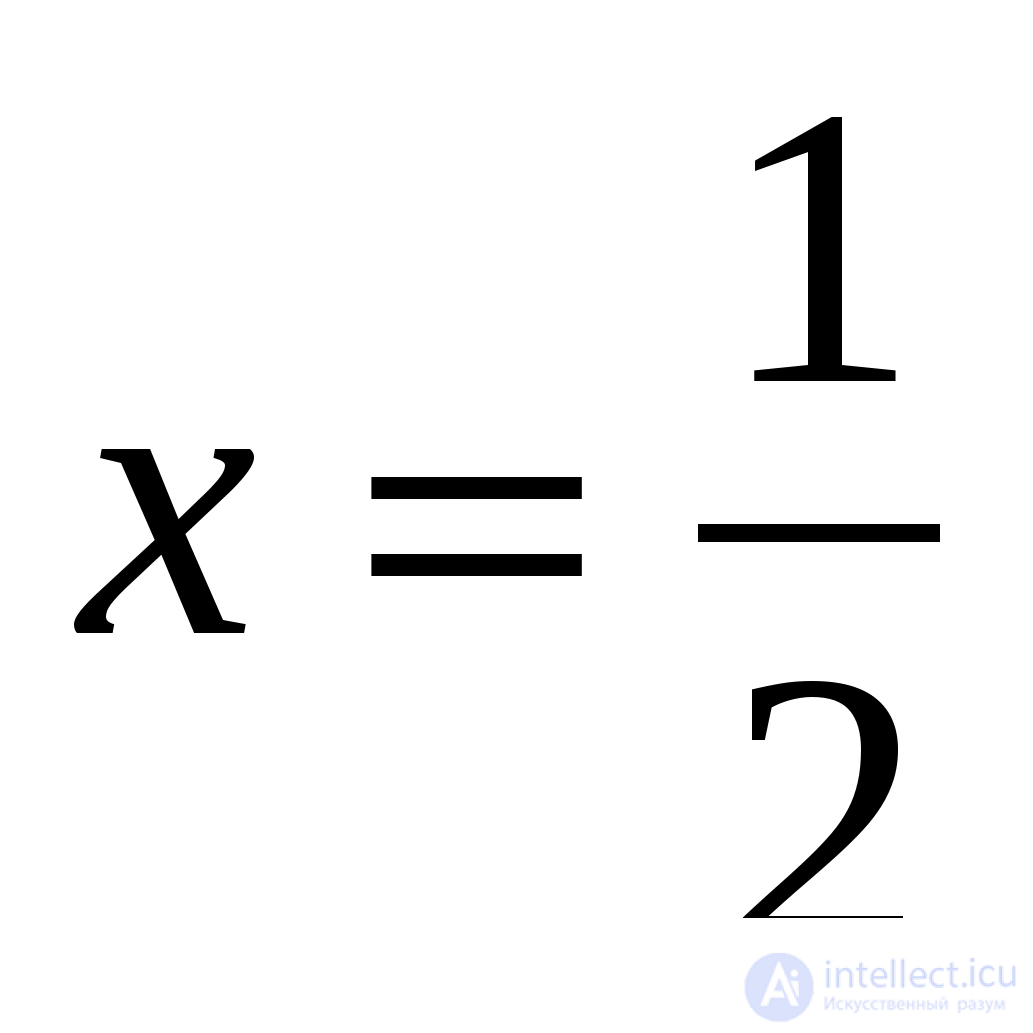 получаем, что
получаем, что 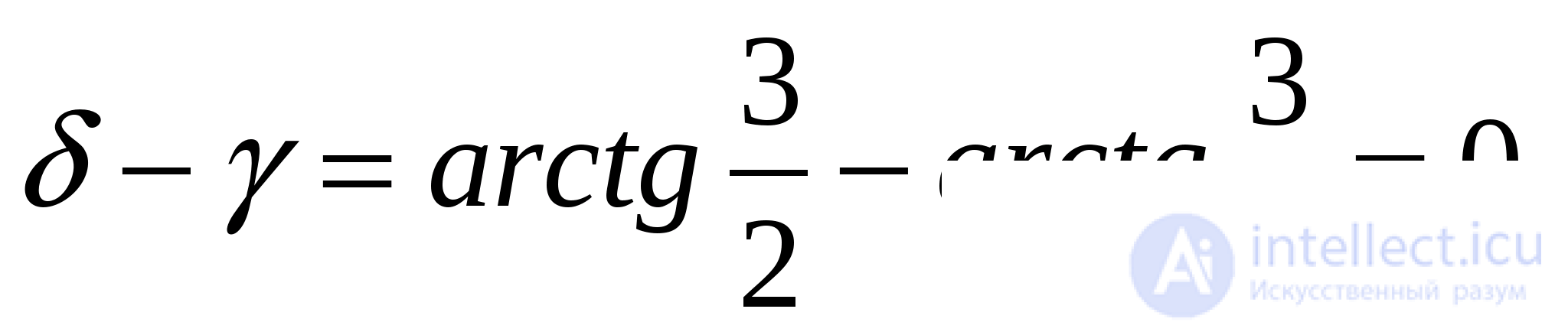 Таким образом,
Таким образом, 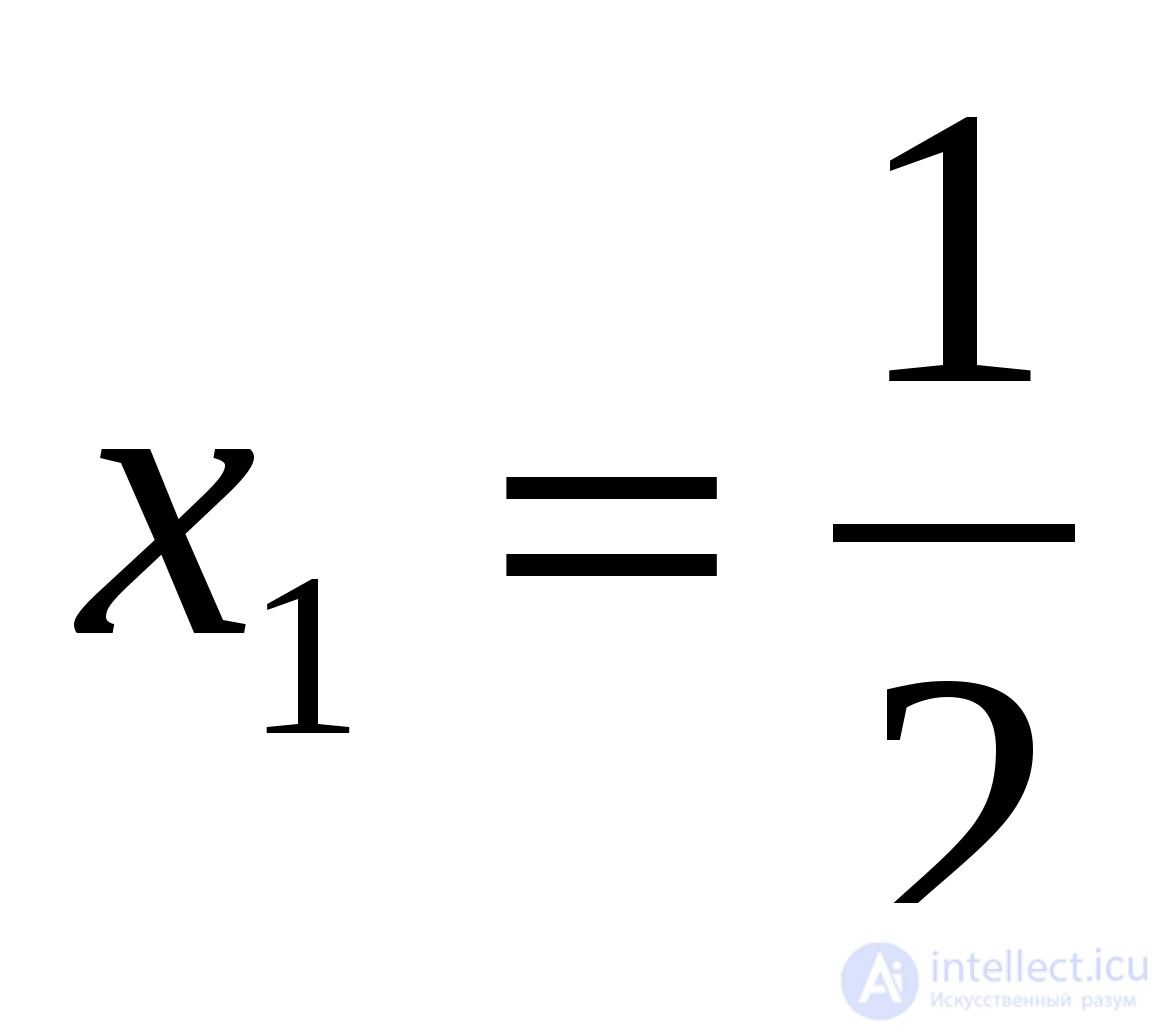 - корень уравнения.
- корень уравнения.
Если  то от обеих частей уравнения можно взять котангенсы:
то от обеих частей уравнения можно взять котангенсы:

Что приведет к следствию исходного уравнения. Раскрыв скобки и подставив выражения тригонометрических функций 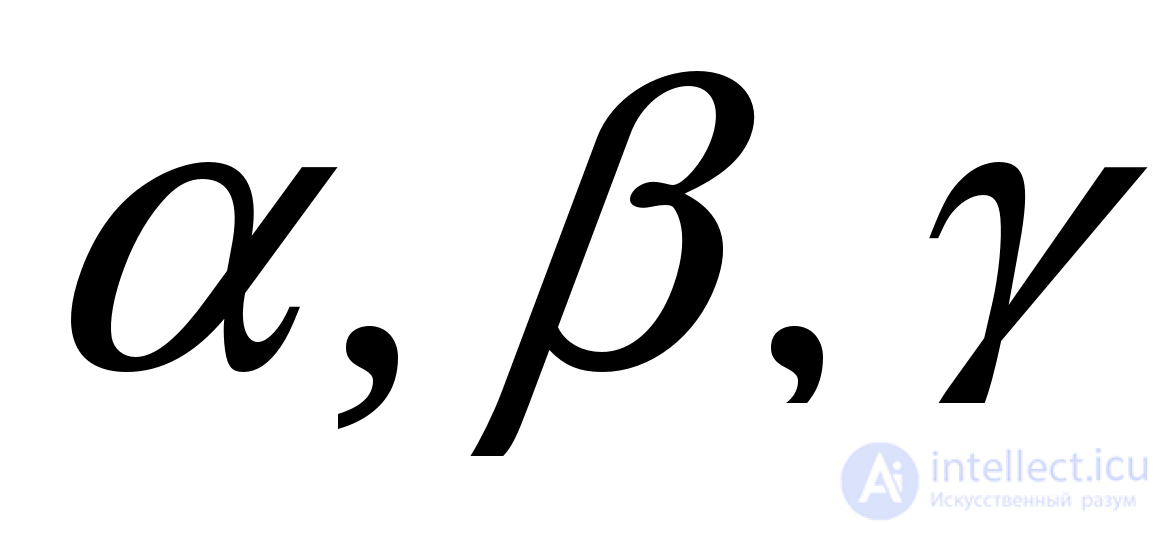 и
и  через
через  получим уравнение
получим уравнение

которое равносильно системе
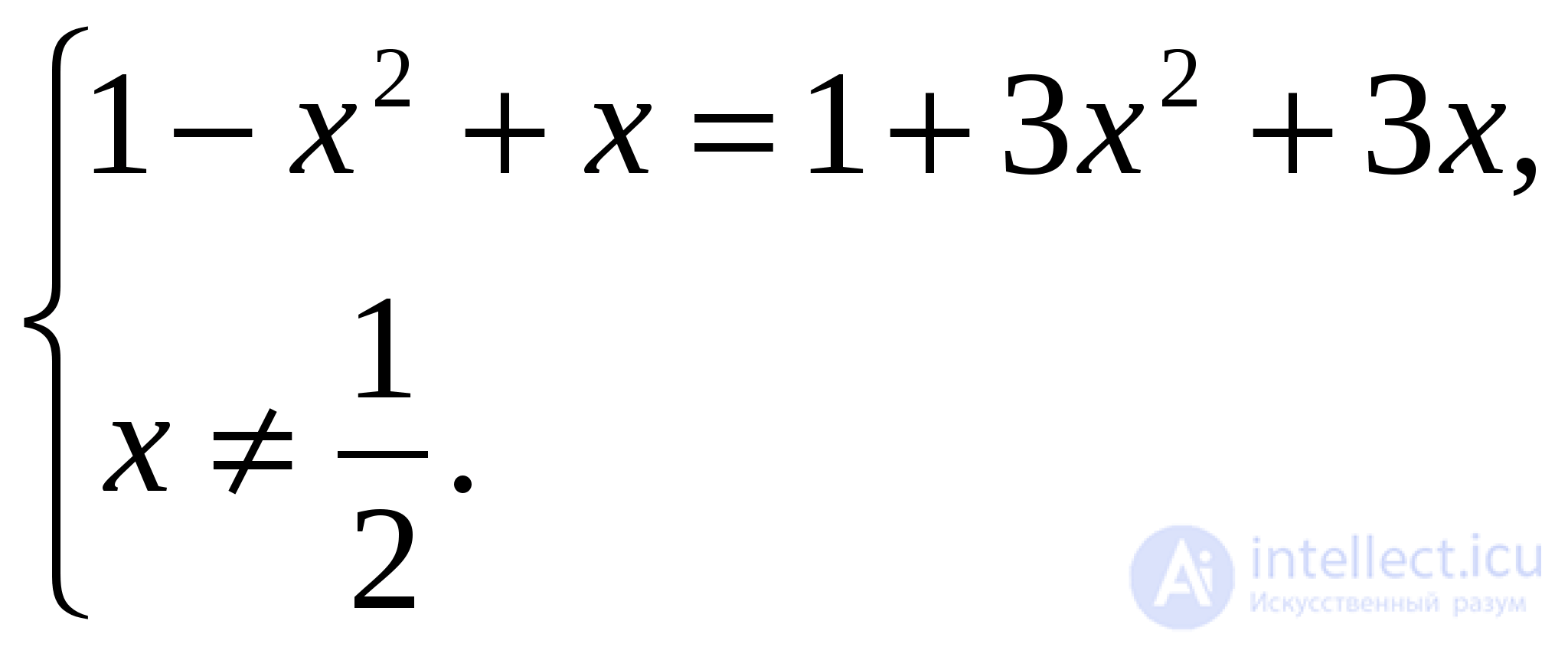
Получаем два значения неизвестного: 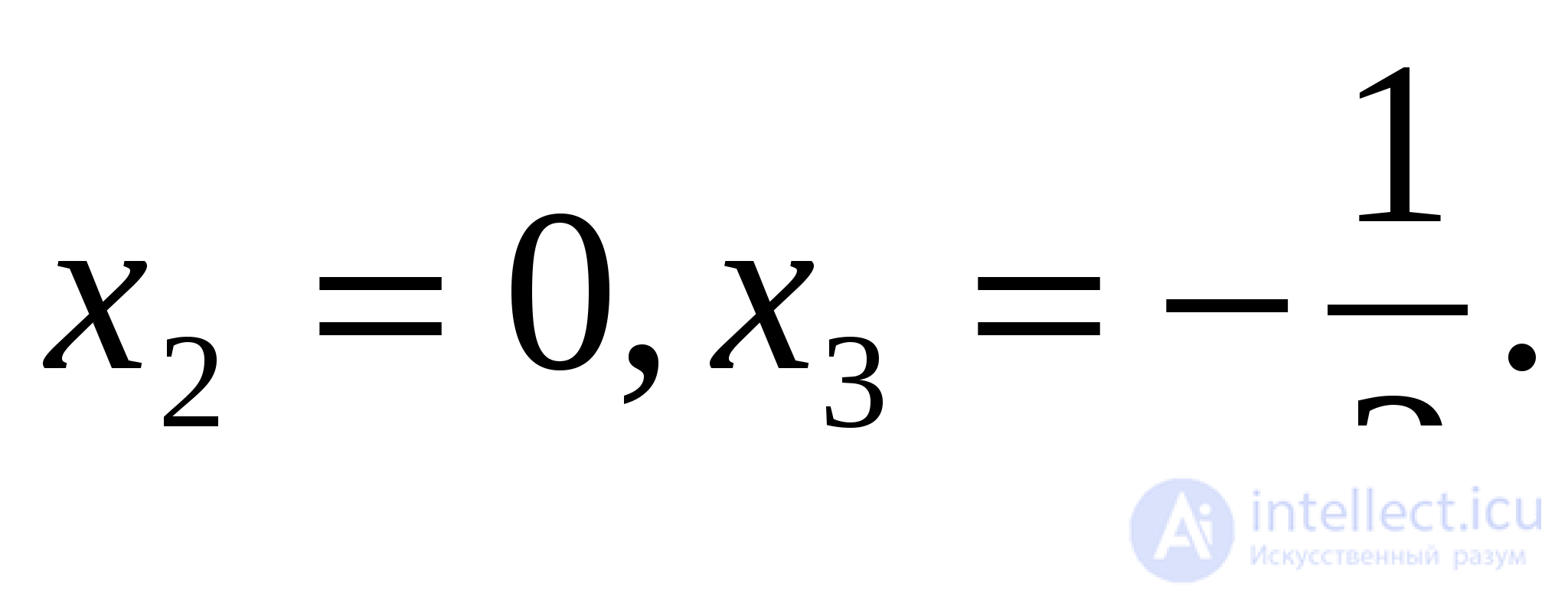 Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.
Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.
Подход (III): Для упрощения исходного уравнения во многих случаях удобно переходить от одних аркфункций к другим (например, от арксинуса или арккосинуса к арктангенсу). При этом, наряду с формулами (14), можно использовать следующие формулы:
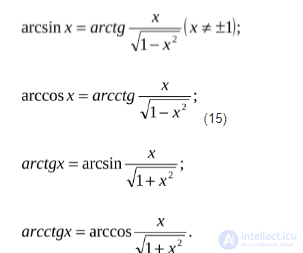
Задача 8. Решить уравнение:
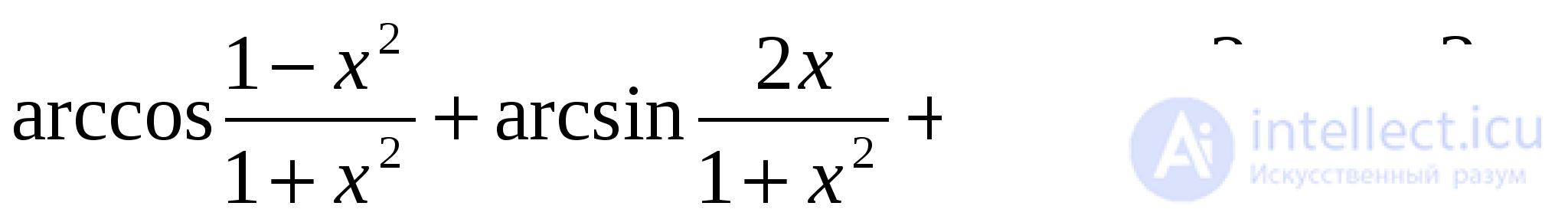
Решение: Заметим, что 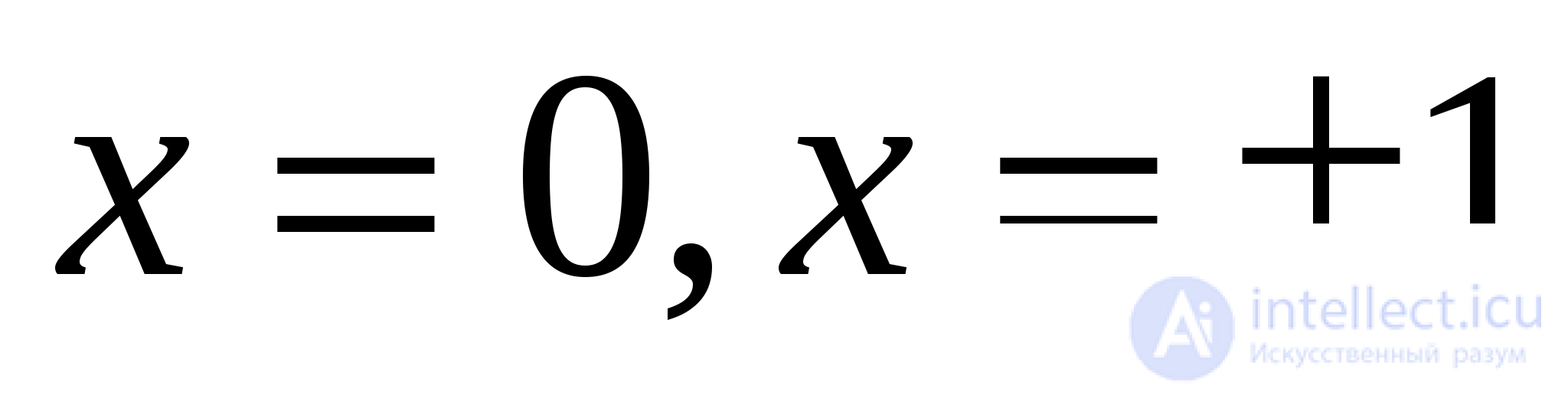 не удовлетворяет данному уравнению. Поэтому, в силу формул (15),
не удовлетворяет данному уравнению. Поэтому, в силу формул (15),

Итак, исходное уравнение можно записать в виде:
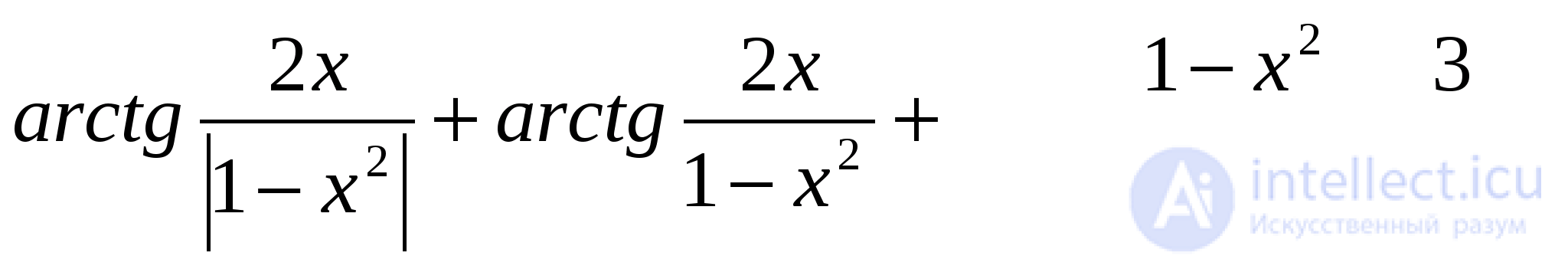
Если  то уравнение принимает вид:
то уравнение принимает вид:
 что невозможно.
что невозможно.
Если  то и в этом случае уравнение
то и в этом случае уравнение
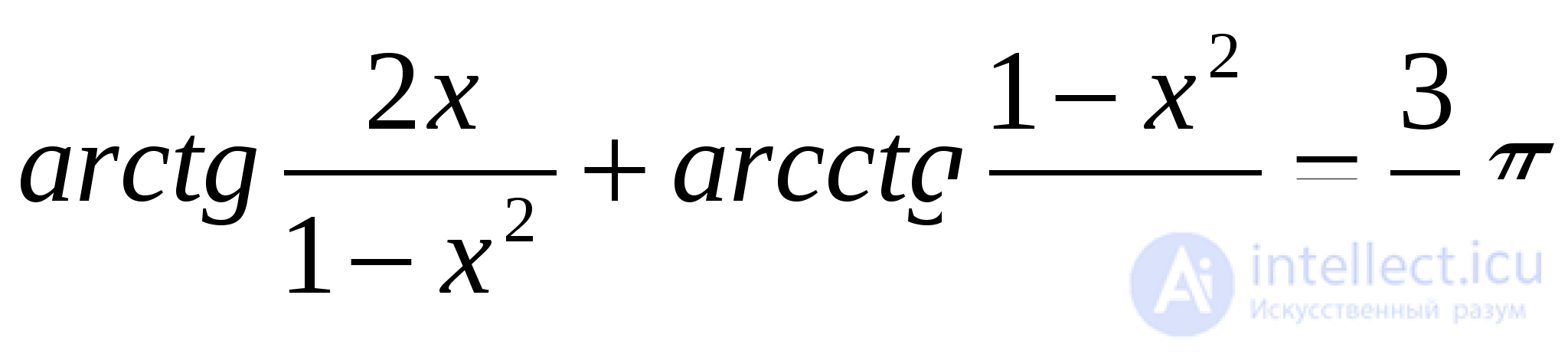 решений не имеет, поскольку
решений не имеет, поскольку
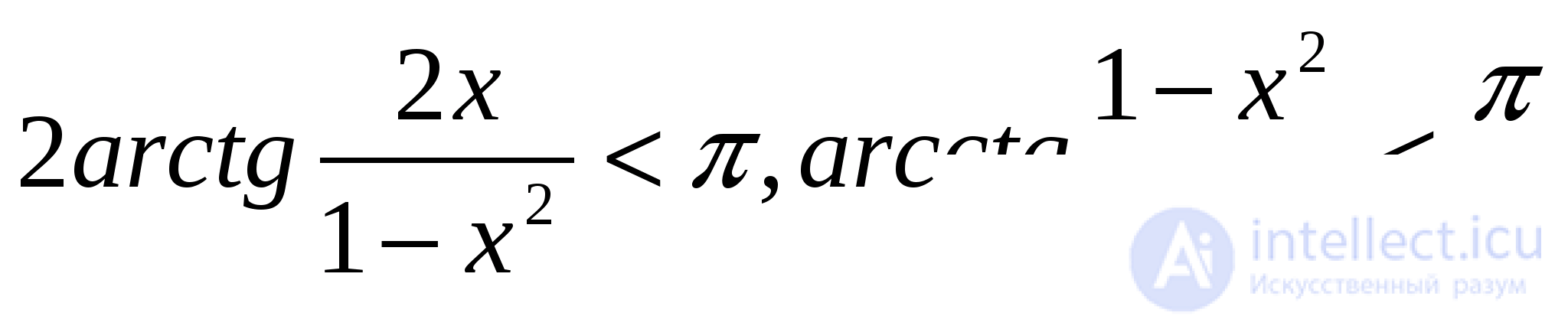 для
для 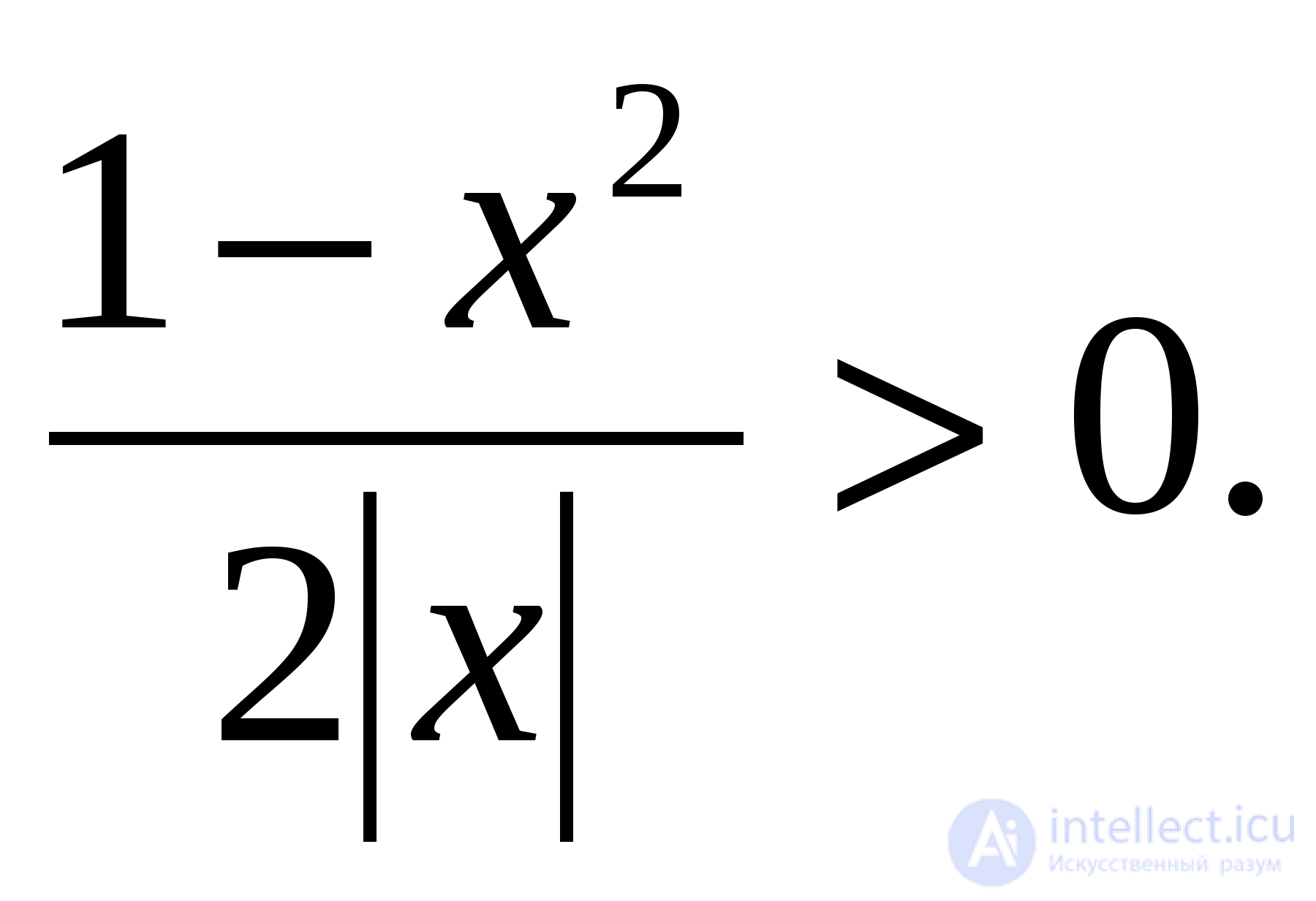
Ответ: нет решений.
Задача 9. Решить уравнение 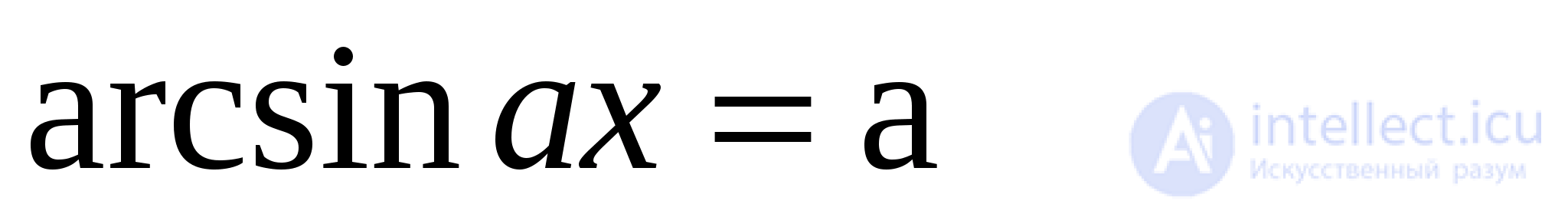
Решение: 
Из полученной системы следует, что 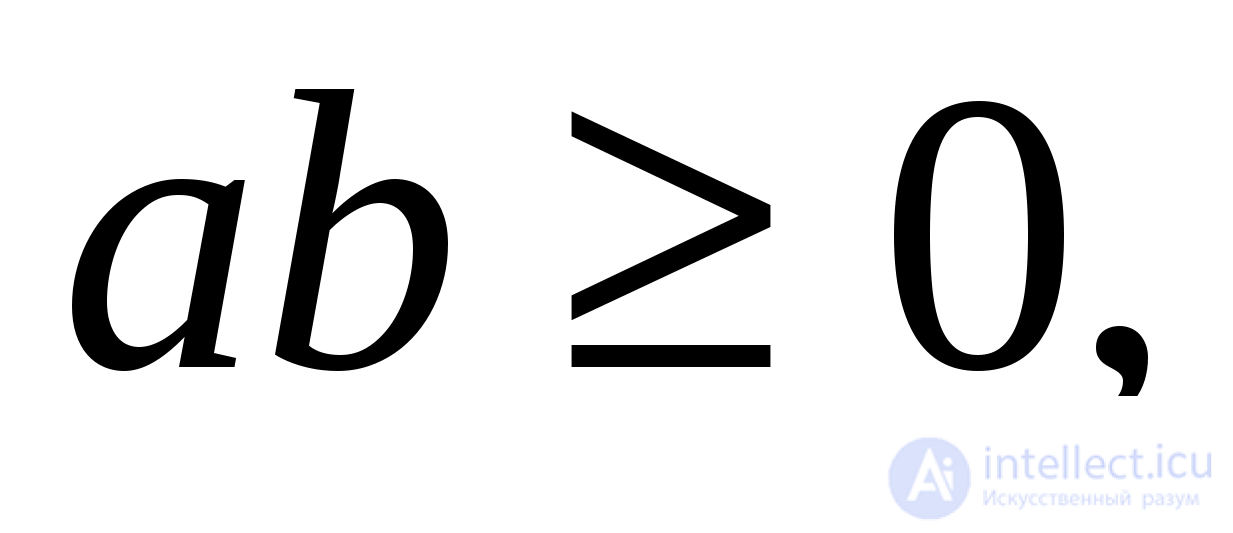 то есть
то есть  и
и  - числа одного знака. Действительно, если
- числа одного знака. Действительно, если 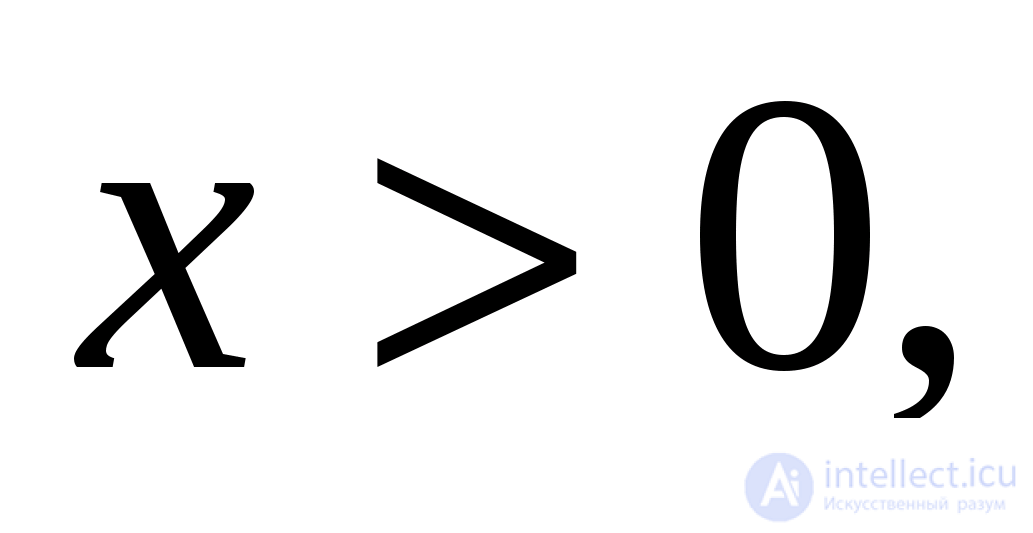 то
то 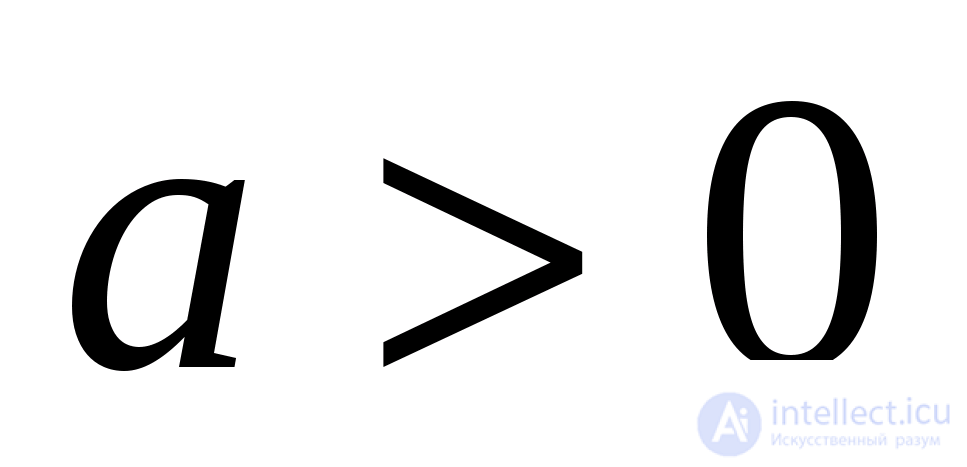 и
и
Если же то из неравенств сразу следует, что 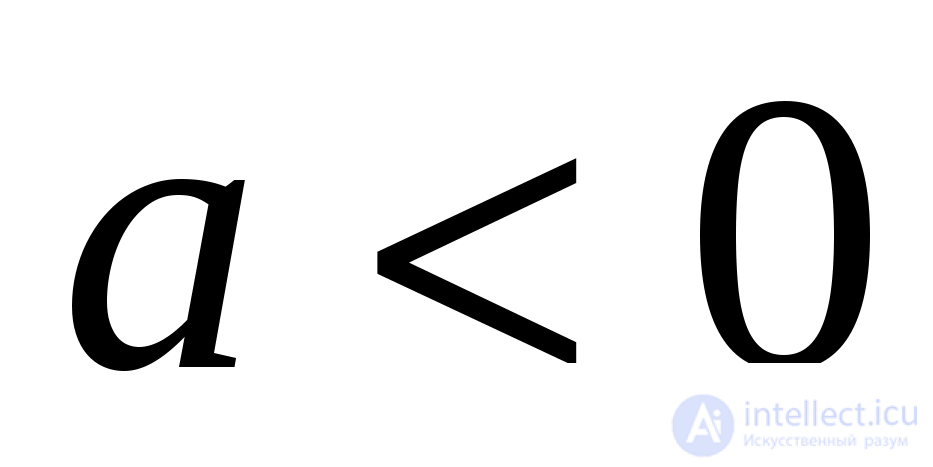 и
и  Следовательно, если
Следовательно, если 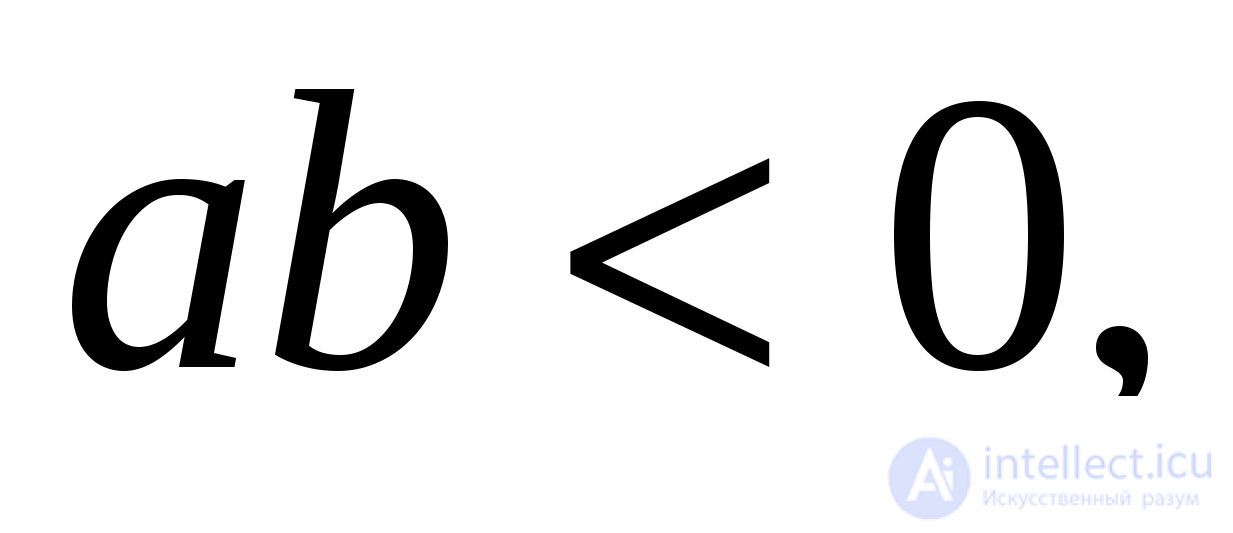 то уравнение решений не имеет.
то уравнение решений не имеет.
Если 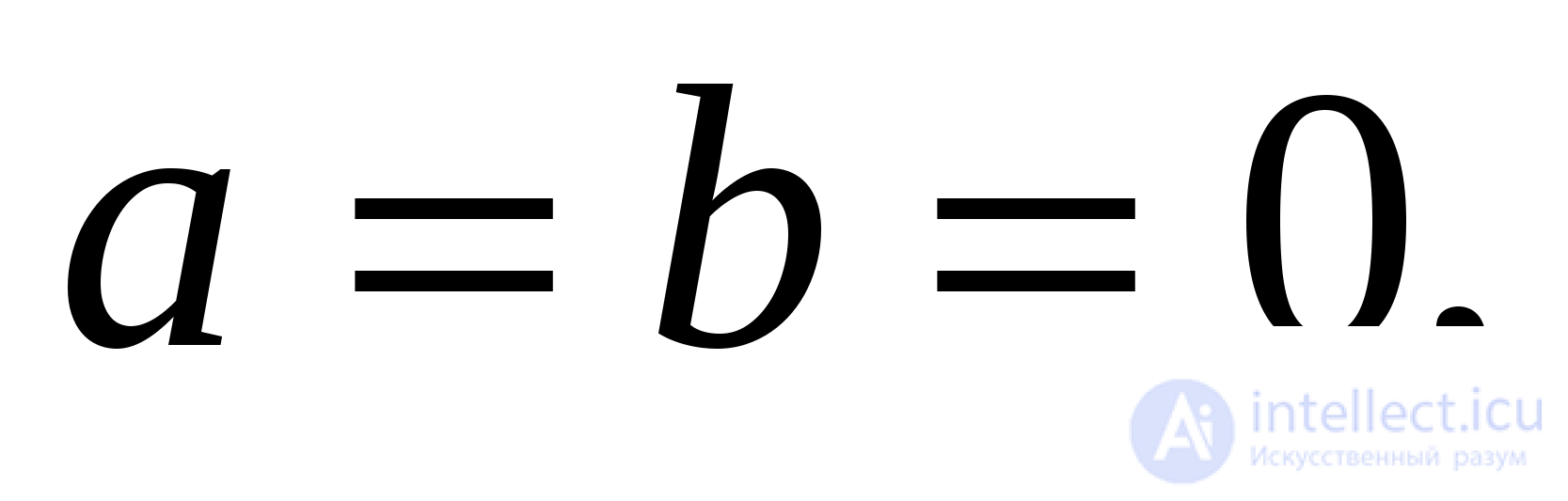 то уравнение также решений не имеет, так как
то уравнение также решений не имеет, так как

Пусть 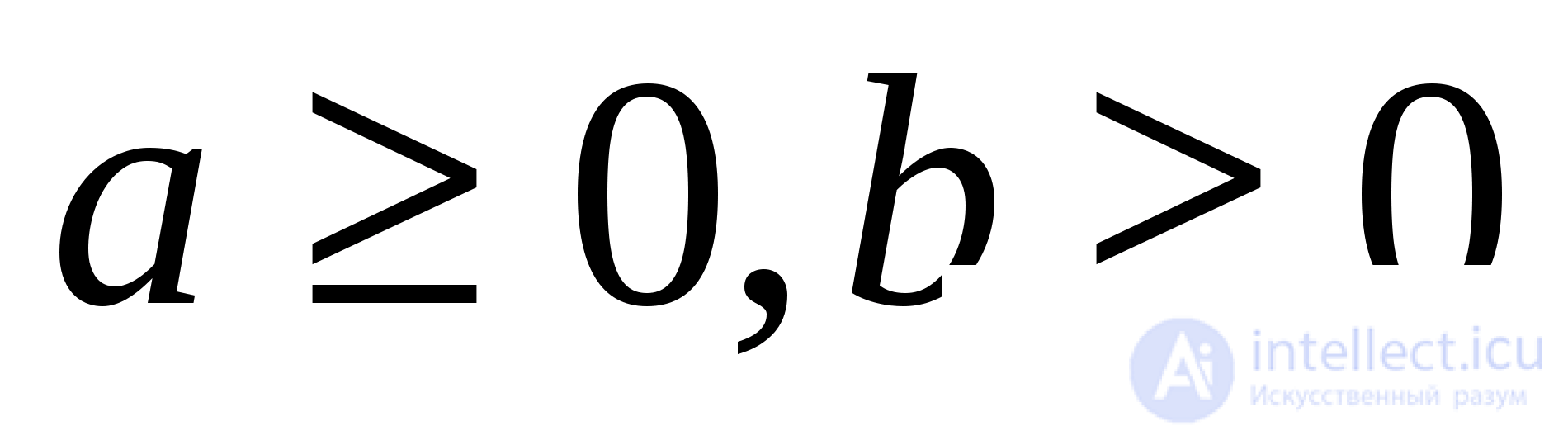 и хотя бы одно из чисел не равно нулю. Тогда получим, что
и хотя бы одно из чисел не равно нулю. Тогда получим, что
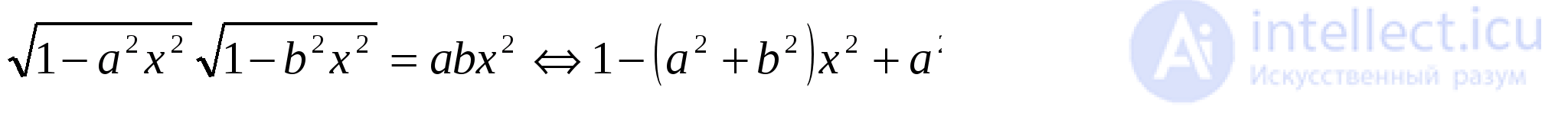
Учитывая ограничения системы, получаем, что если 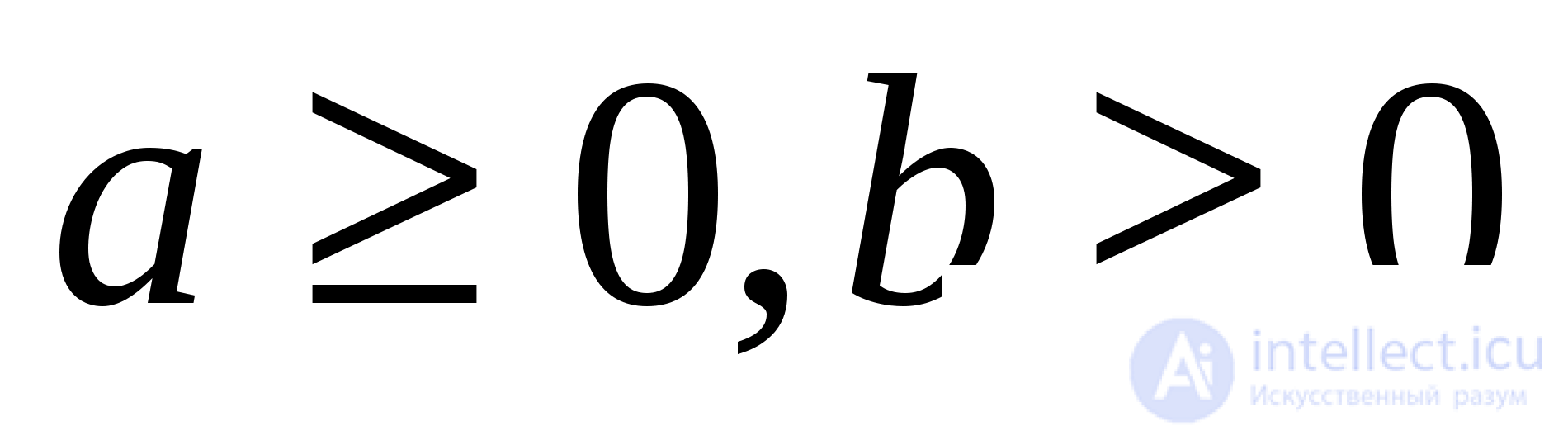 и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 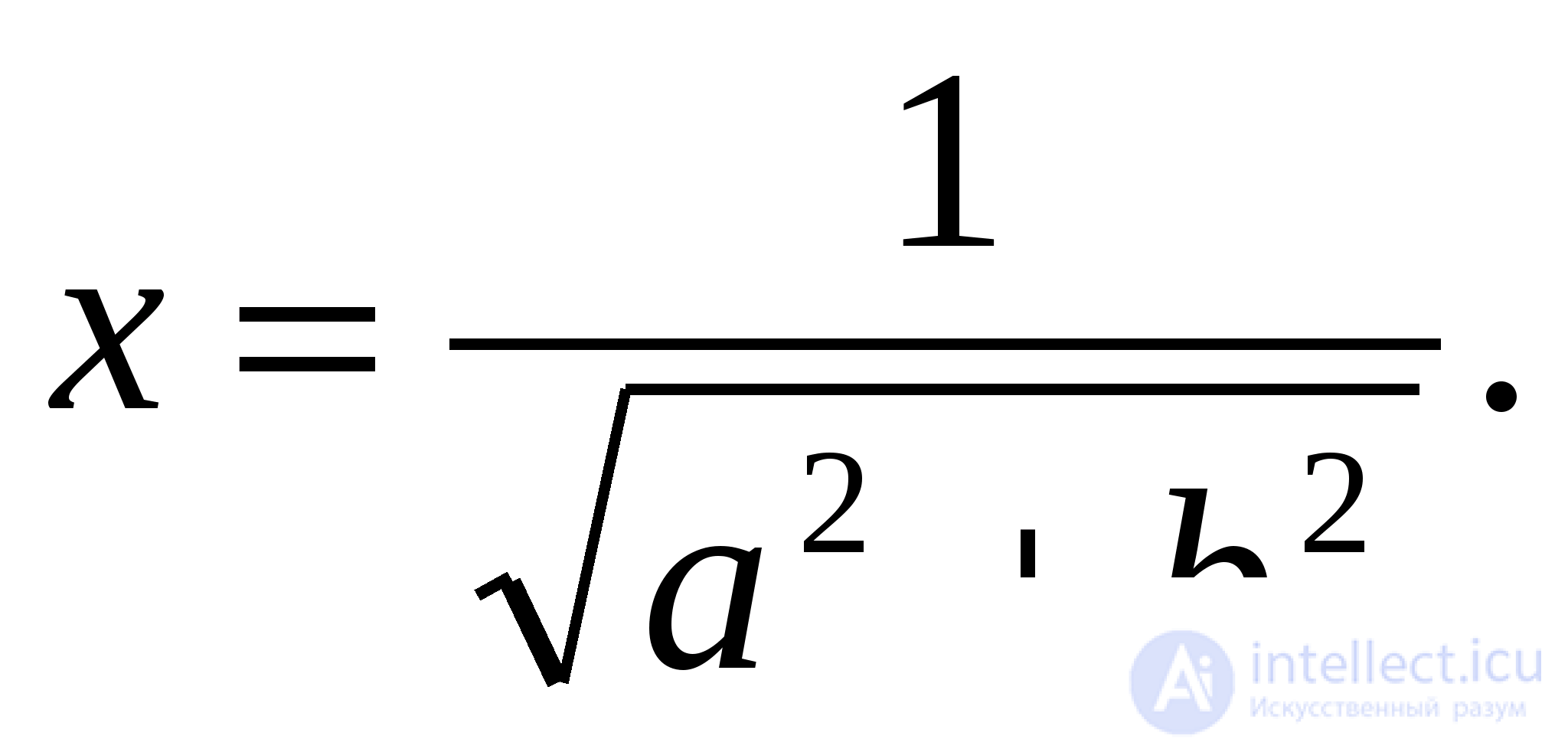
Если же 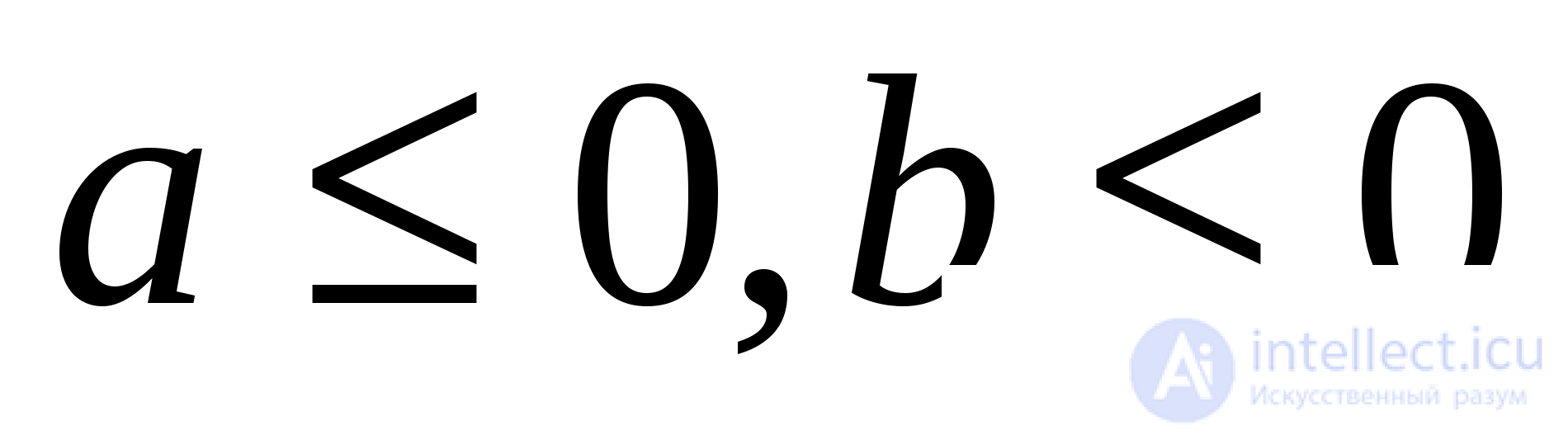 и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 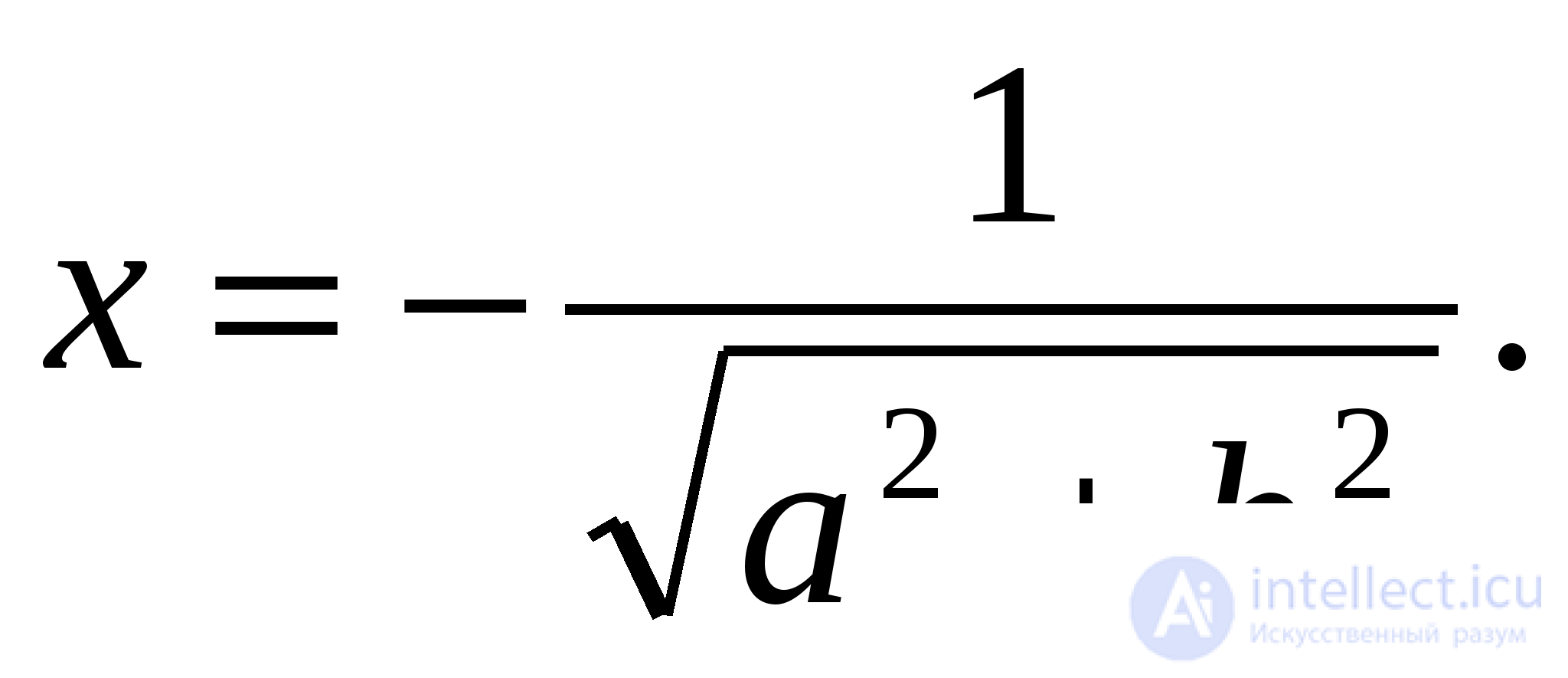
Ответ: если 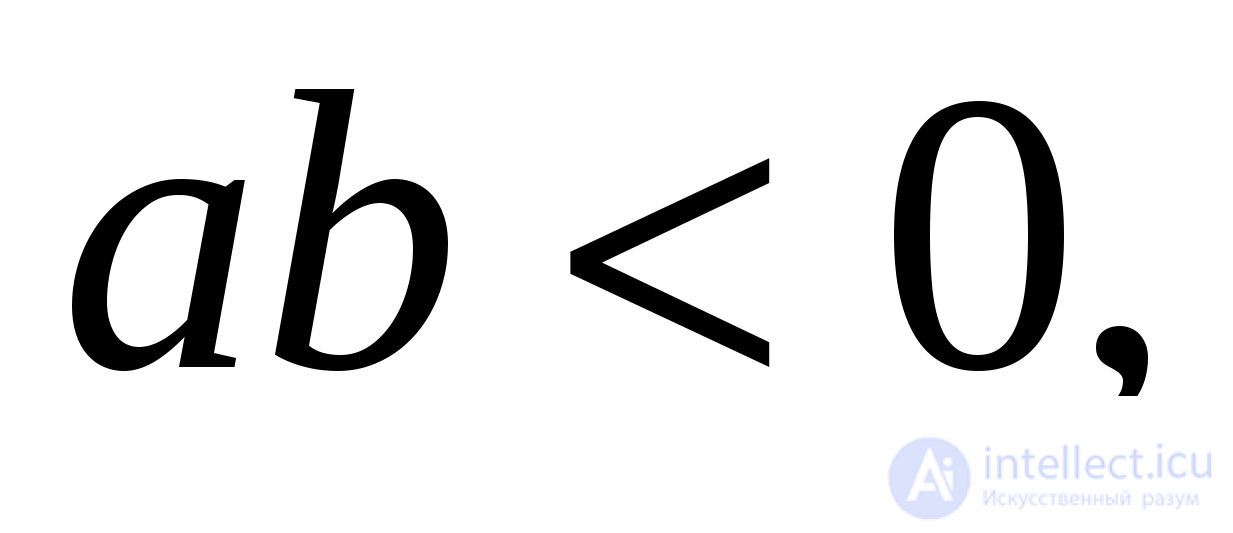 то уравнение решений не имеет; если
то уравнение решений не имеет; если 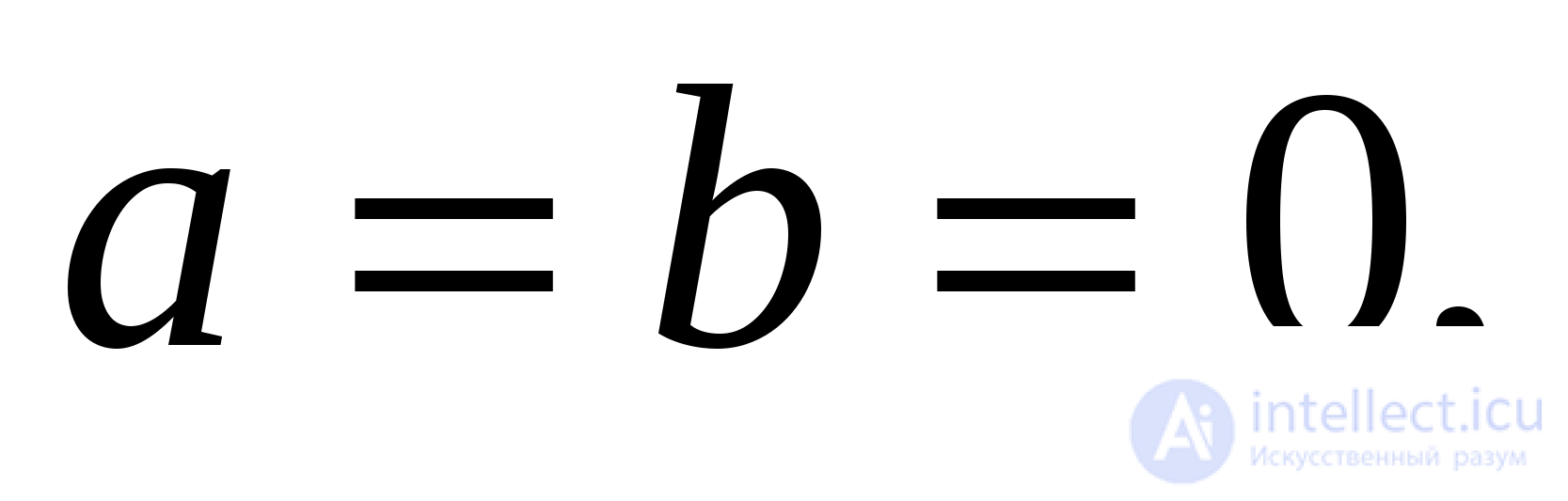 то уравнение решений не имеет; если
то уравнение решений не имеет; если 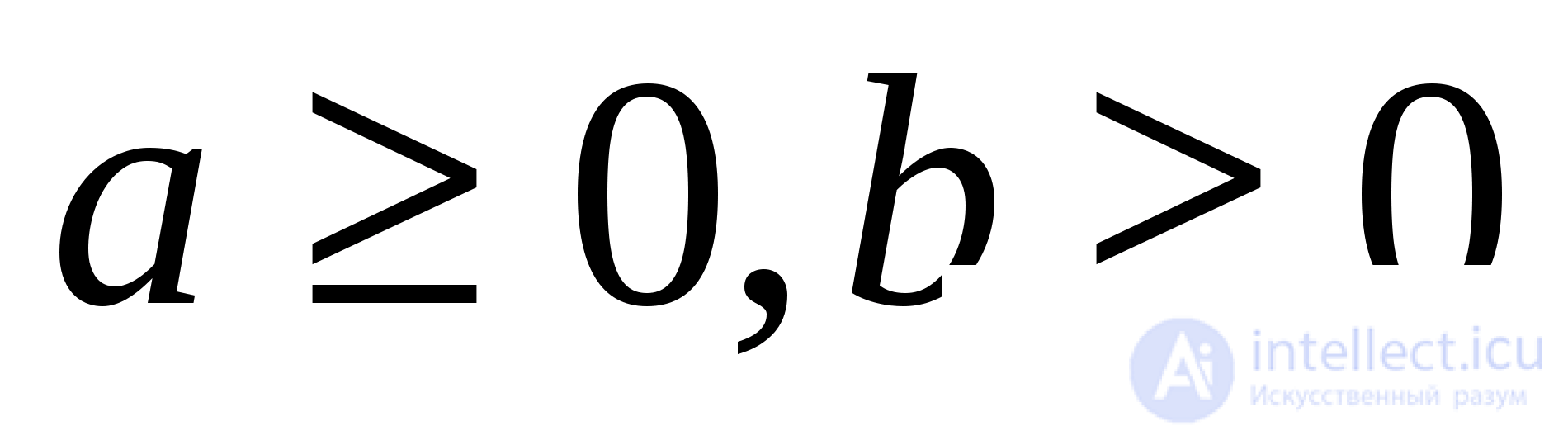 и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 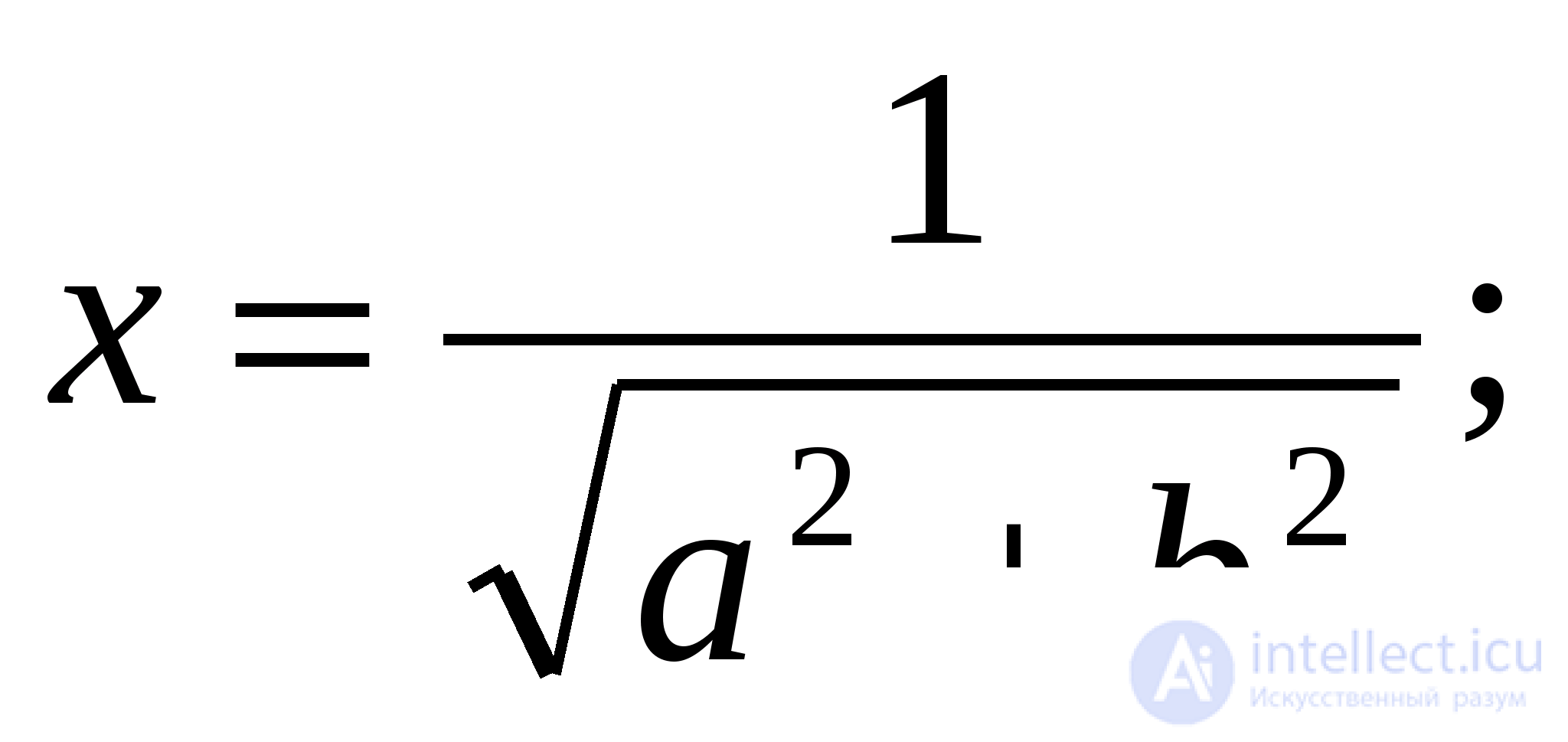 если
если 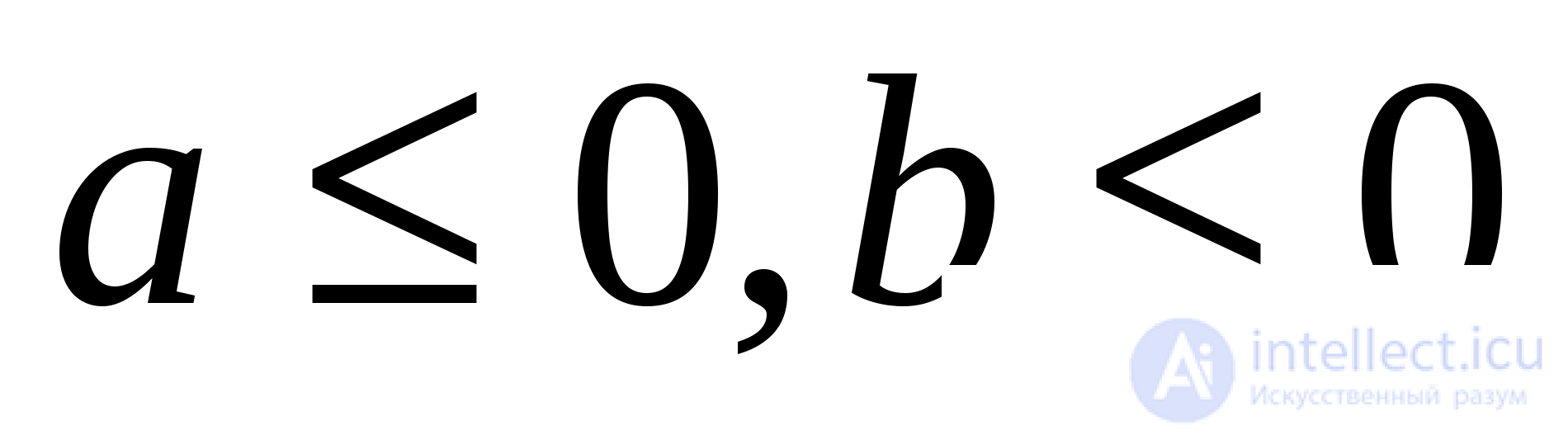 и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 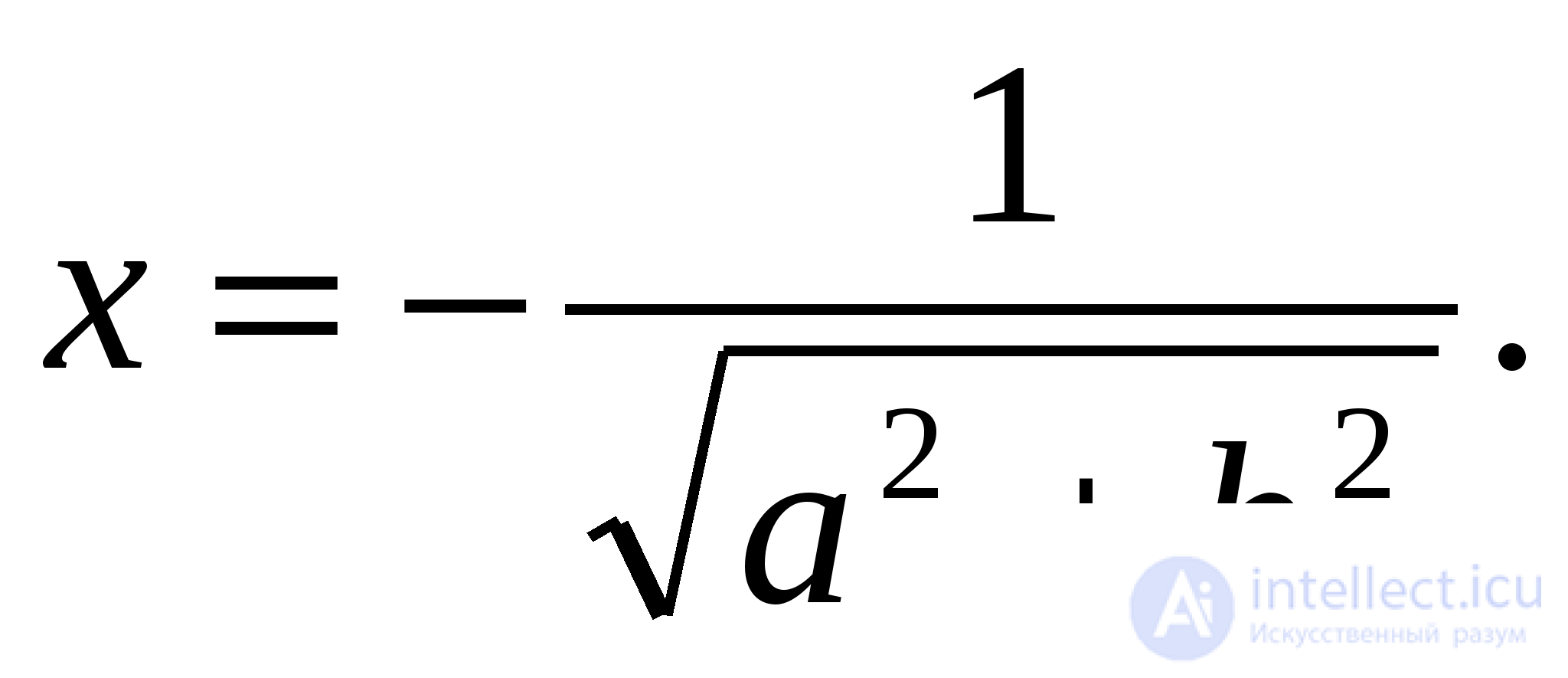
Задача 10. Решить систему уравнений
Решение: Используя формулы группы 2, получим:
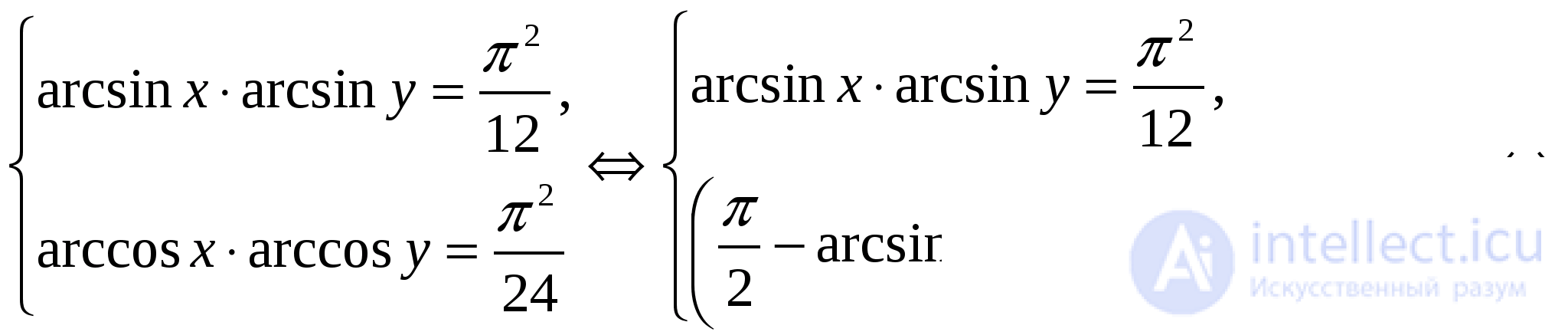
Обращаясь к методам алгебраических систем уравнений, получим, что  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения
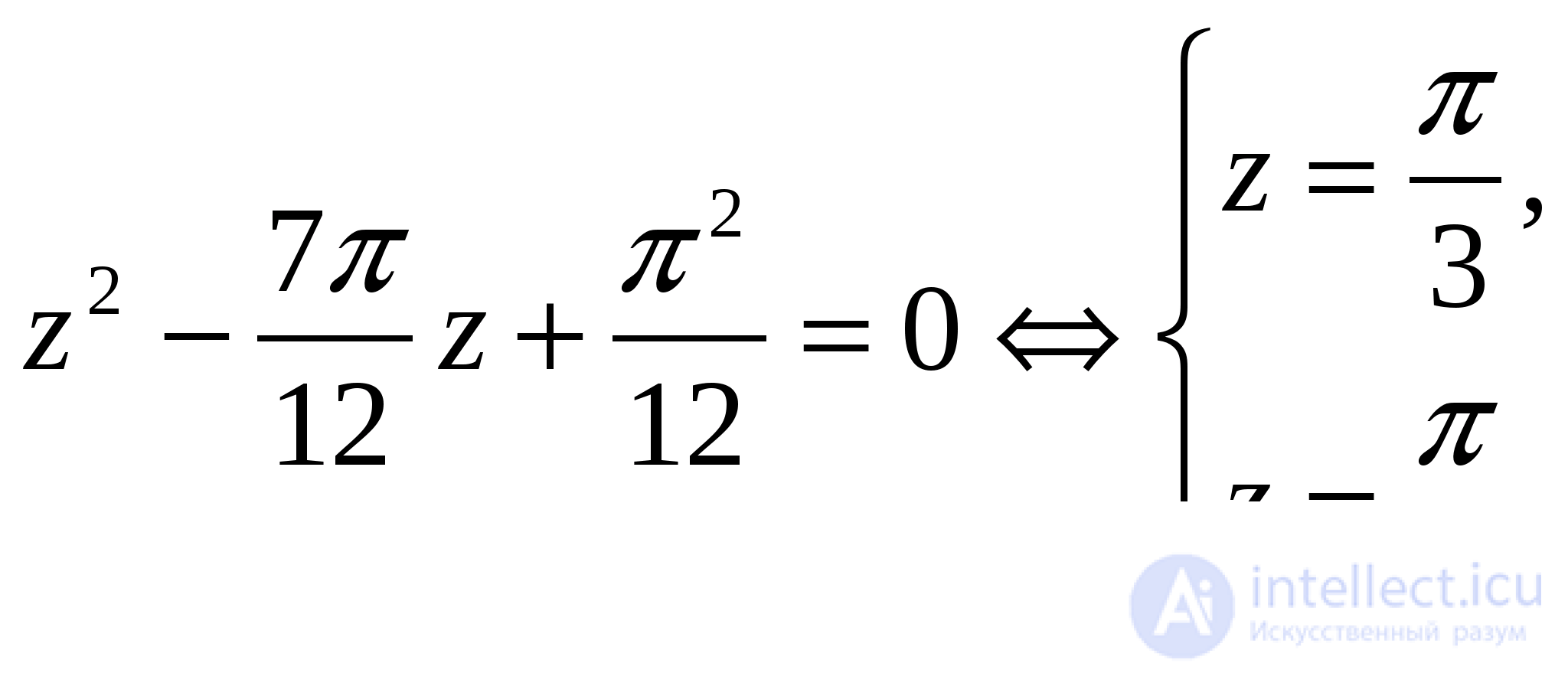
Получим

2.3. Вычисление значений обратных тригонометрических функций
Пример 1. Найдите  если
если 
Решение: Оценим 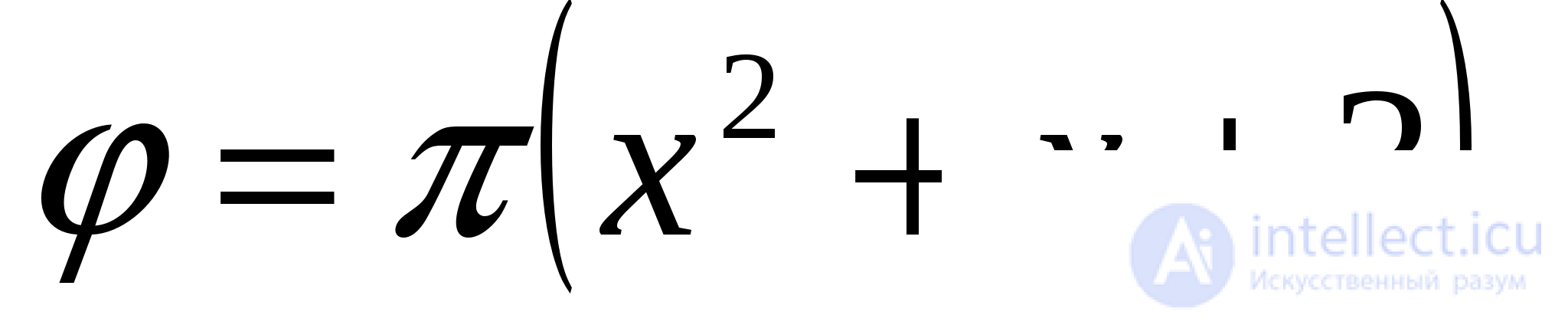 если
если 
Имеем
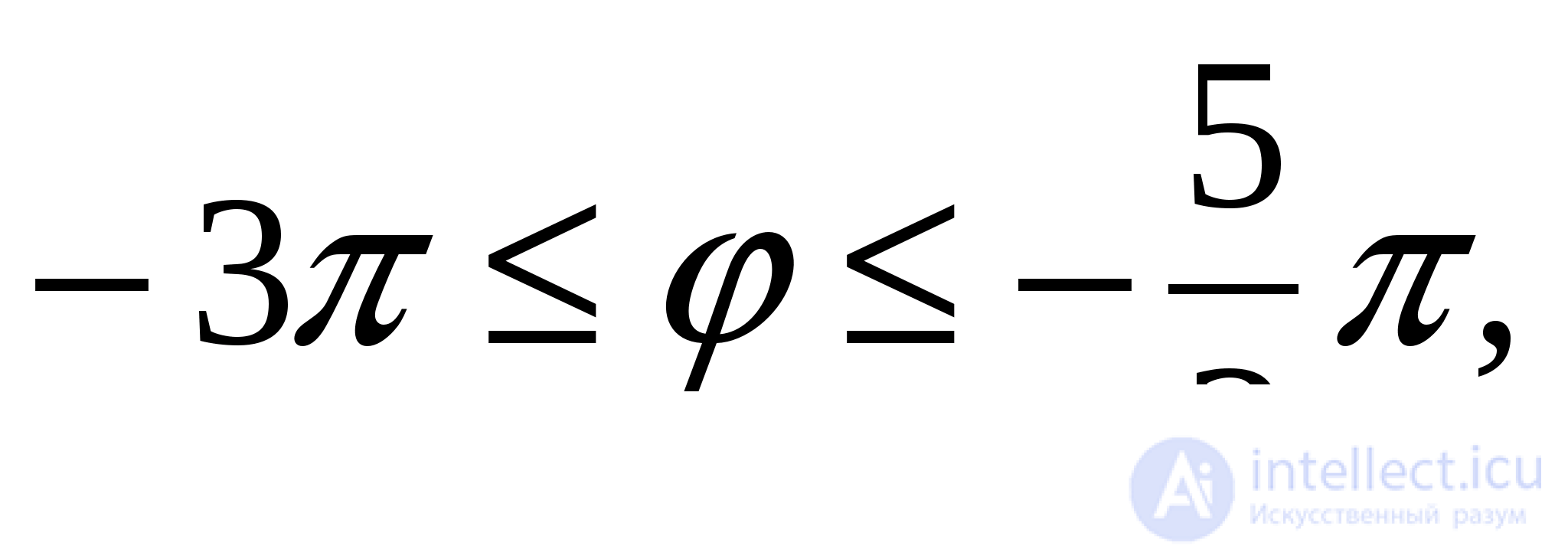 или
или 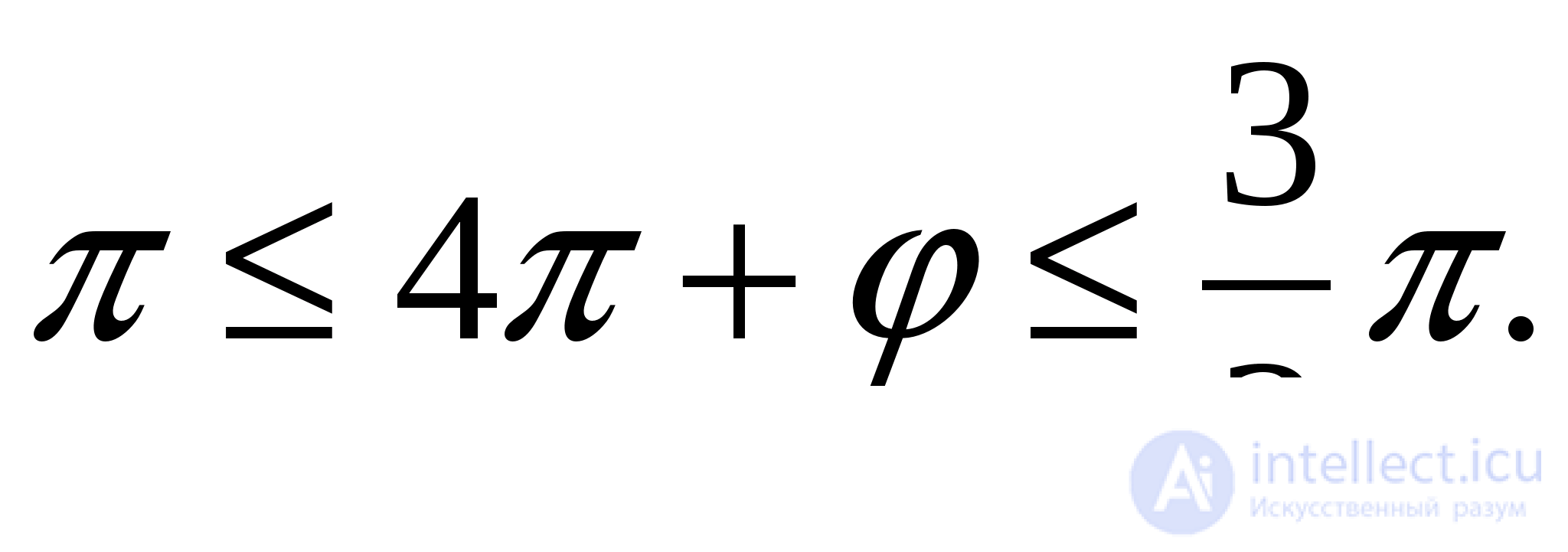
Следовательно,
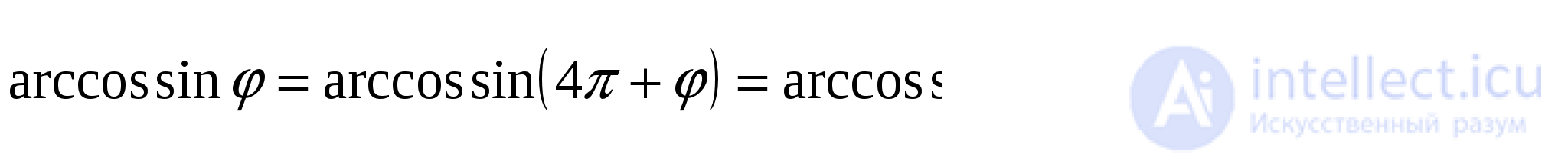

где 
Окончательно получаем

Ответ: 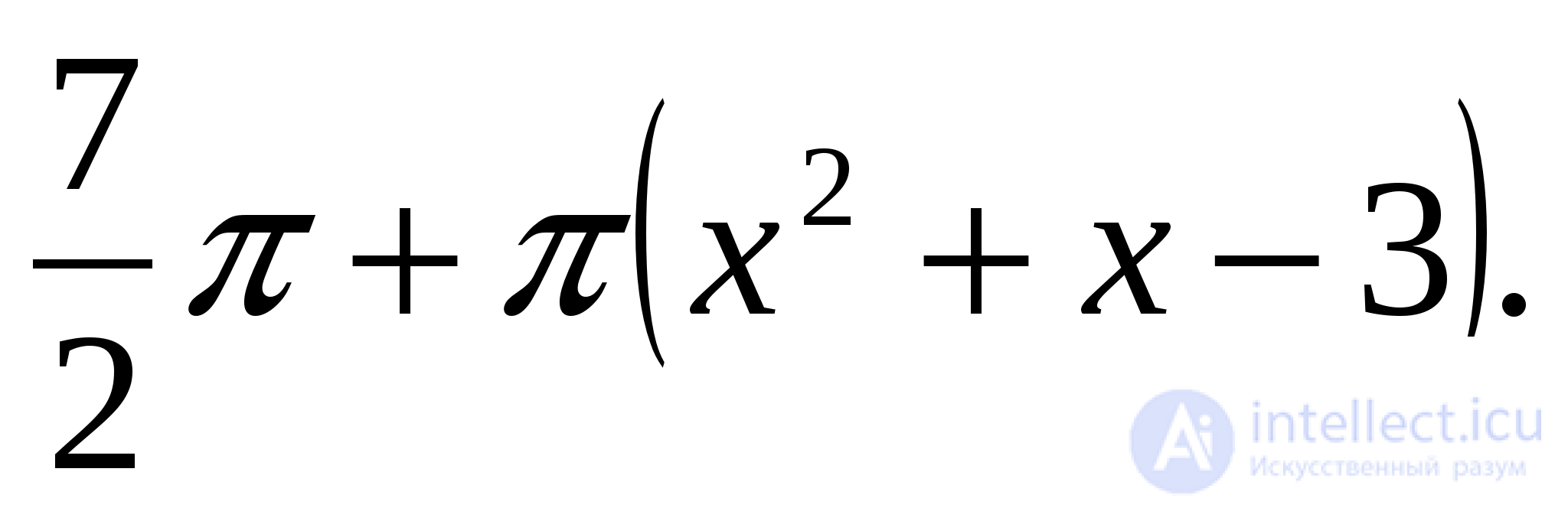
Пример 2. Докажите, что если  то
то 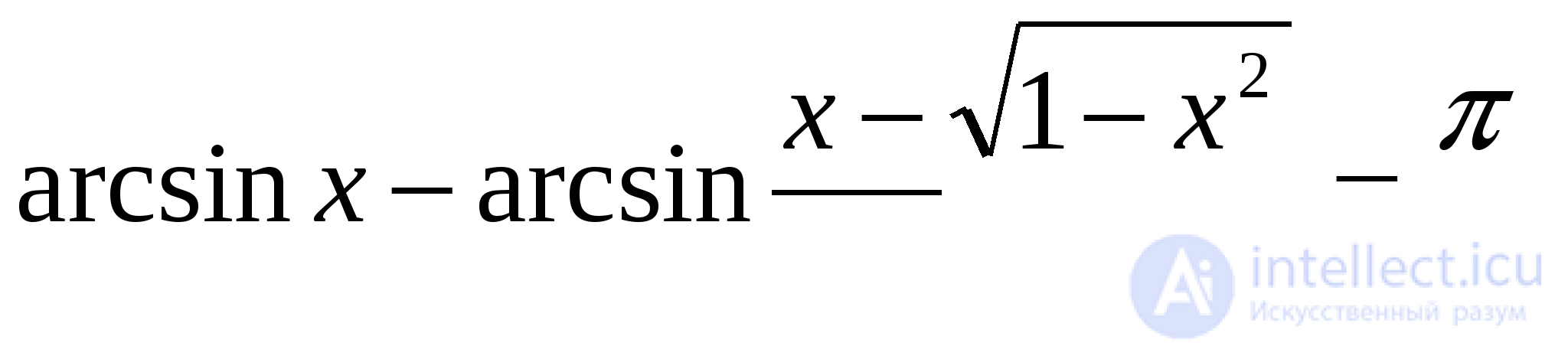
Решение: При  оба арксинуса существуют. Для первого это очевидно, а для второго имеем
оба арксинуса существуют. Для первого это очевидно, а для второго имеем
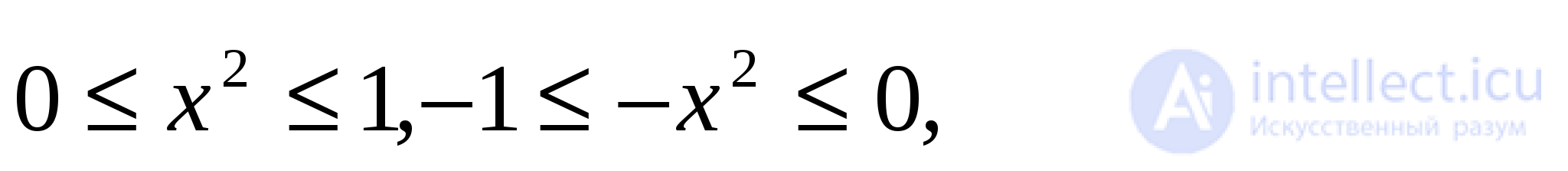
Следовательно,
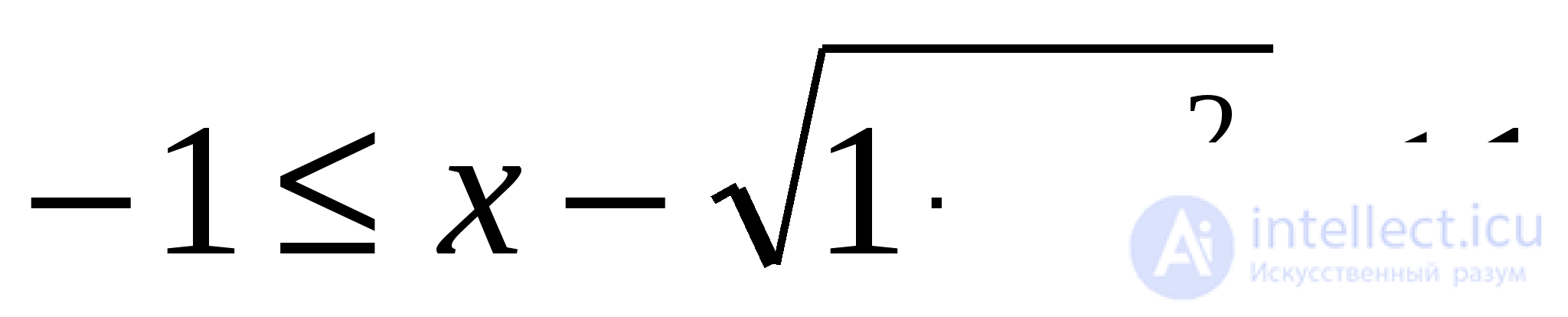
и, тем более,

Введем обозначение
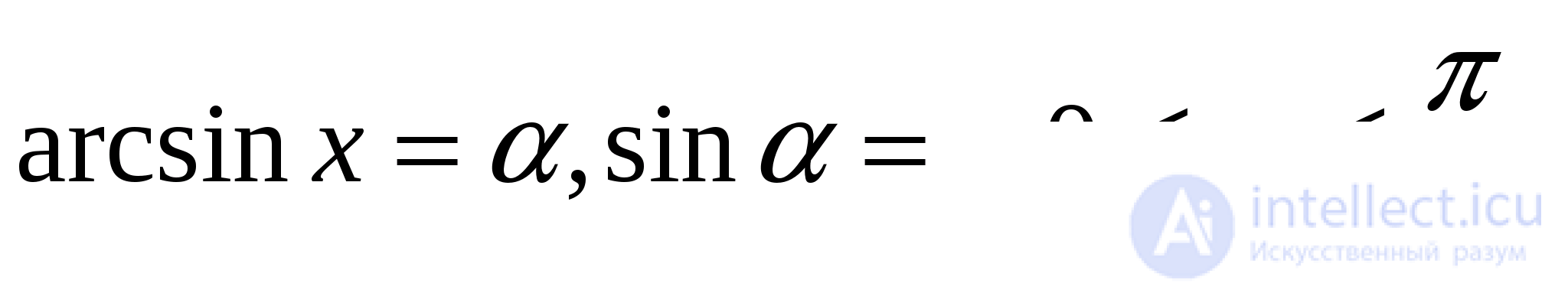
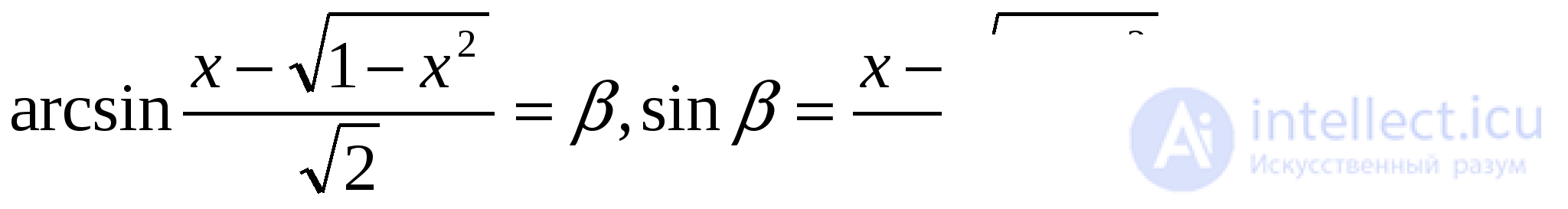
Нужно доказать, что 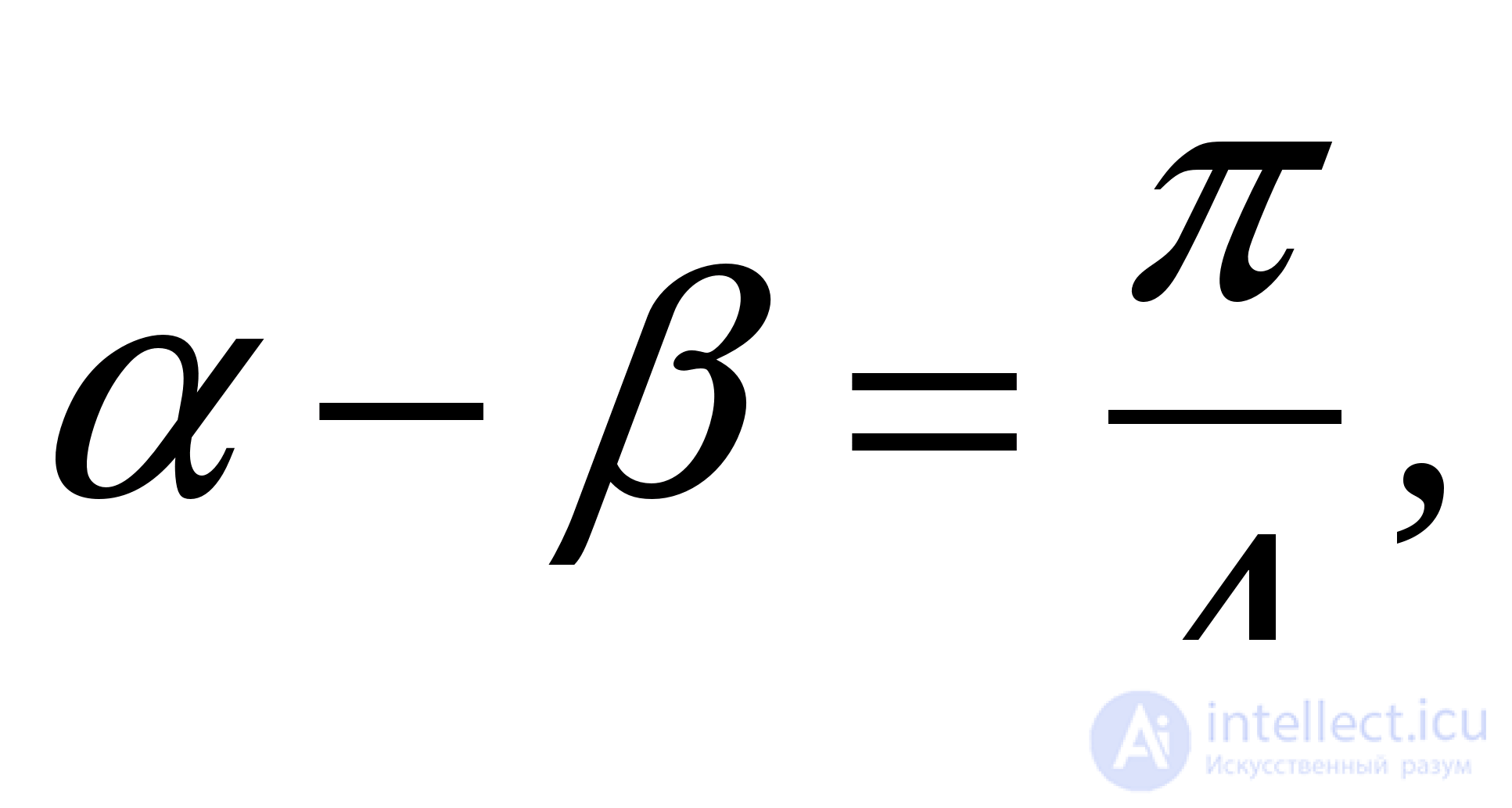 или
или 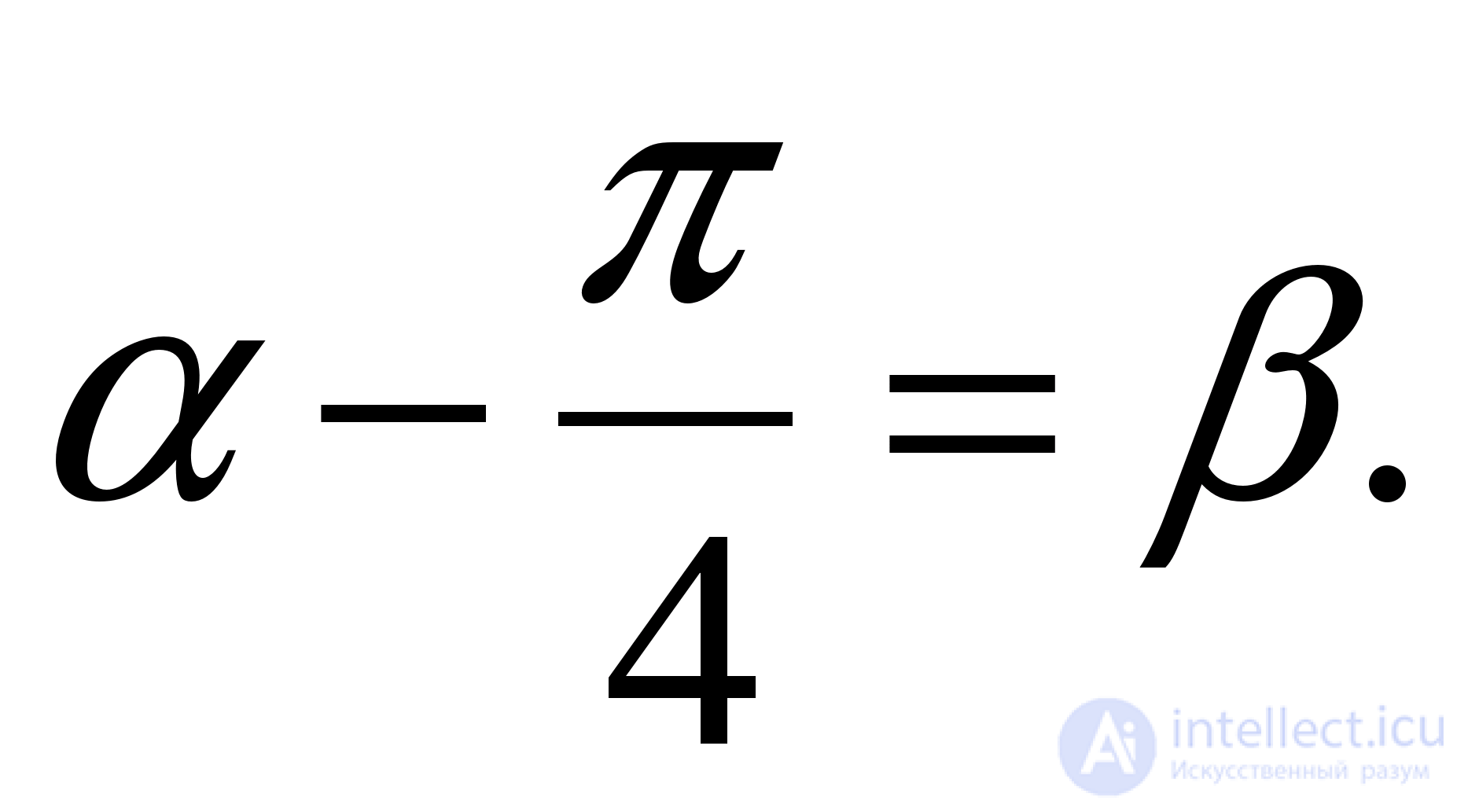 Так как
Так как 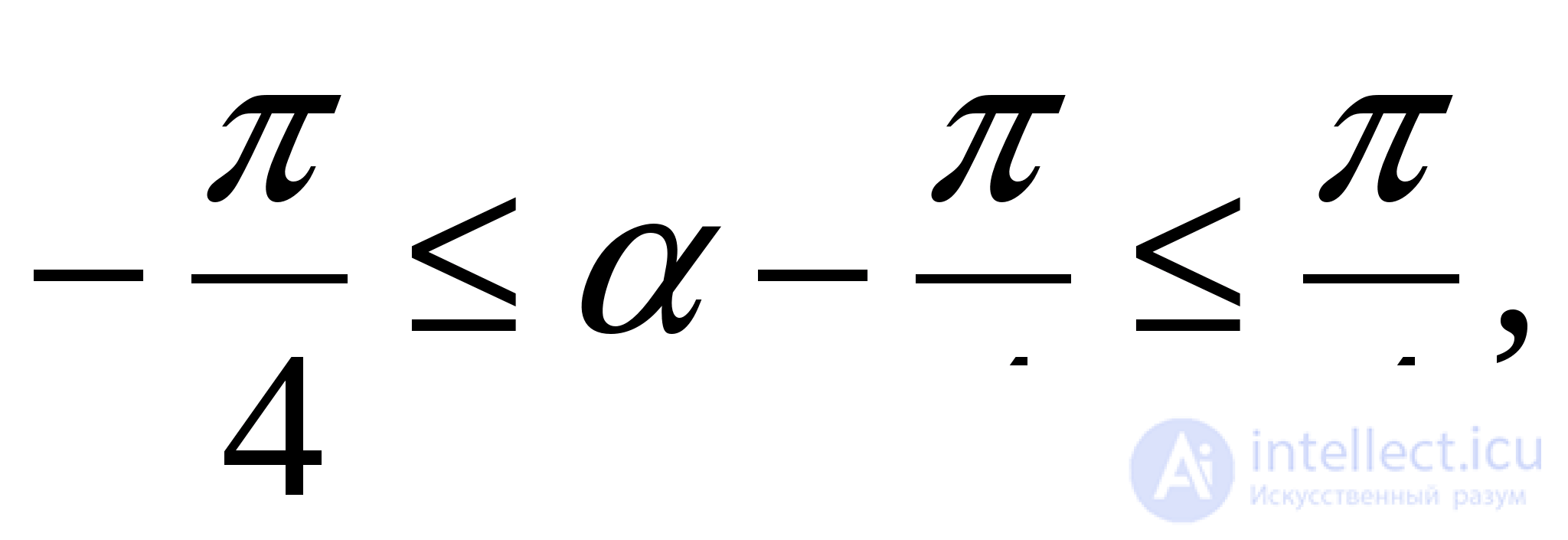 то
то  и
и 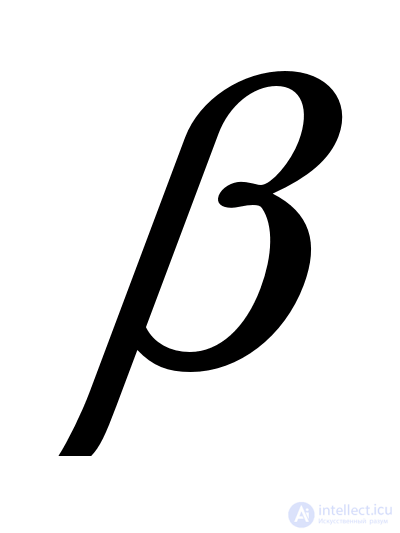 лежат в интервале монотонности синуса. Поэтому, если мы докажем, что синусы этих аргументов равны, то тем самым будет доказано и равенство самих аргументов. Поскольку
лежат в интервале монотонности синуса. Поэтому, если мы докажем, что синусы этих аргументов равны, то тем самым будет доказано и равенство самих аргументов. Поскольку
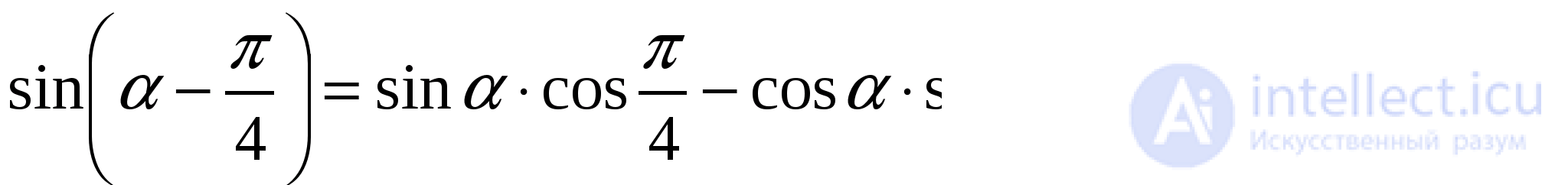
(перед корнем взят знак плюс, так как 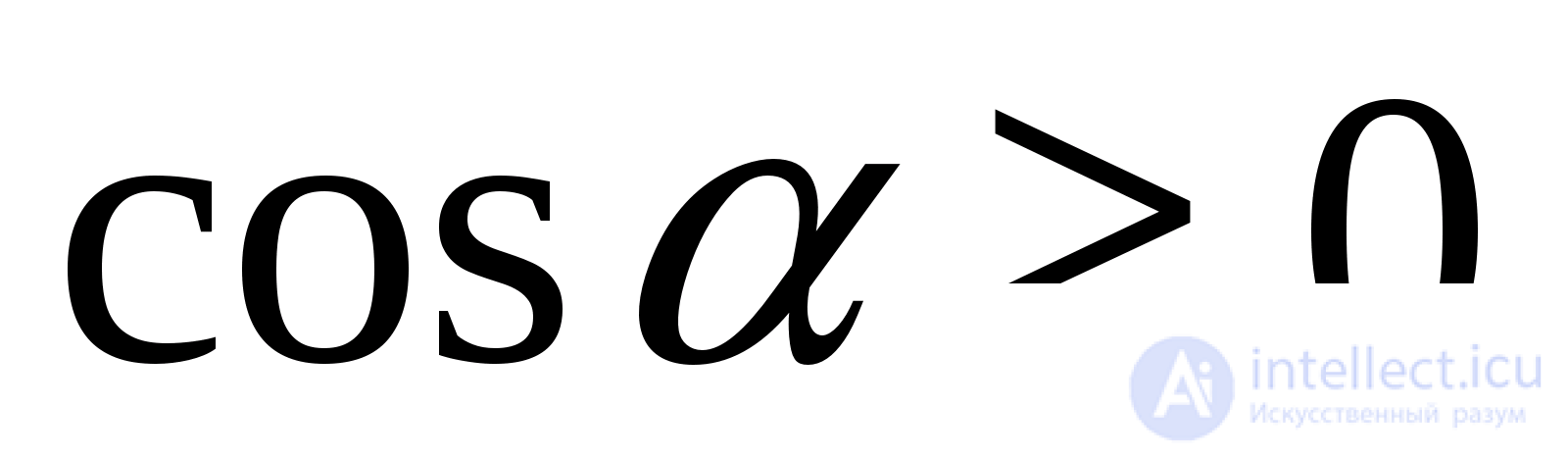 при
при 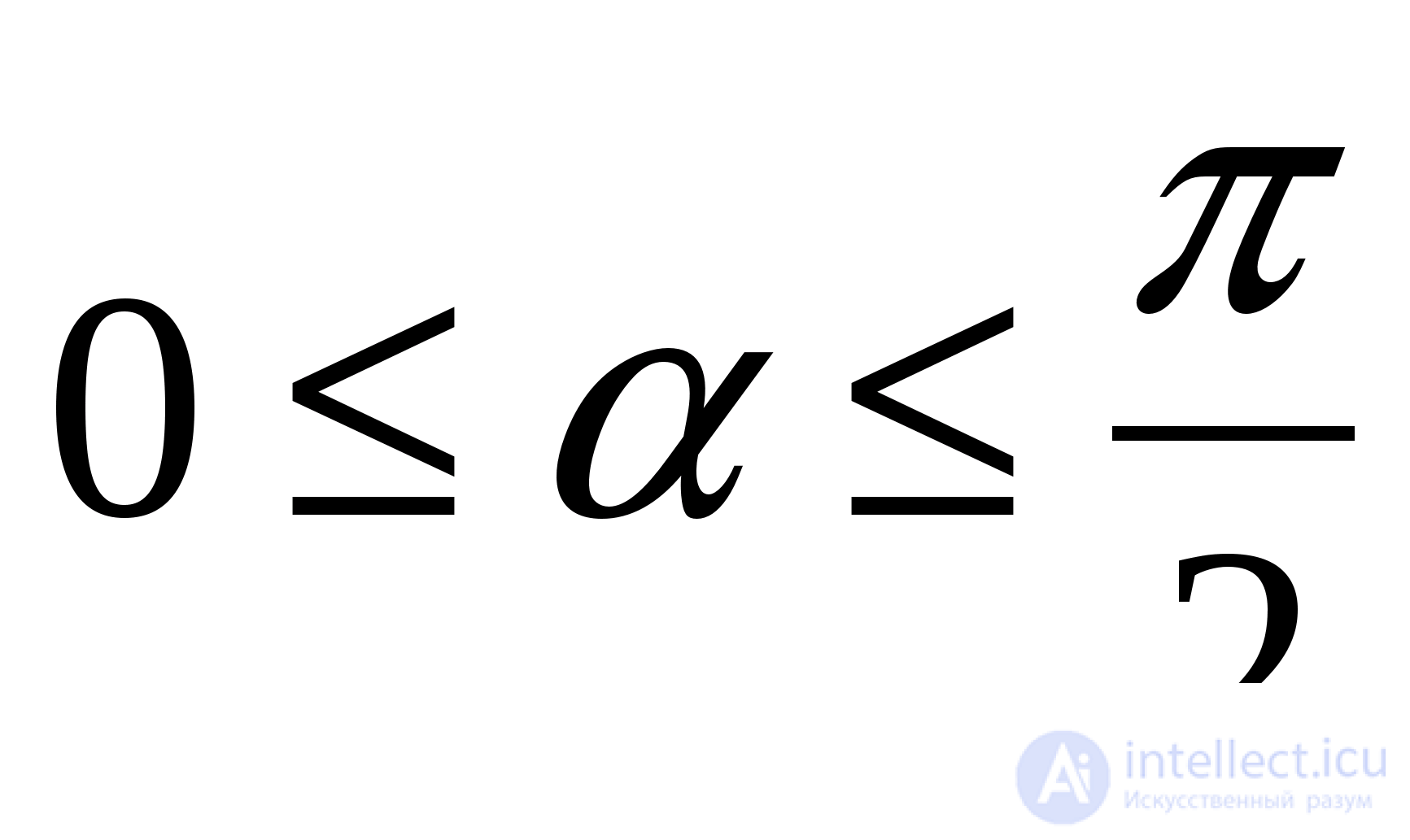 ).
).
Итак, доказано, что  откуда следует справедливость равенства.
откуда следует справедливость равенства.
Пример 3. Докажите, что выражение 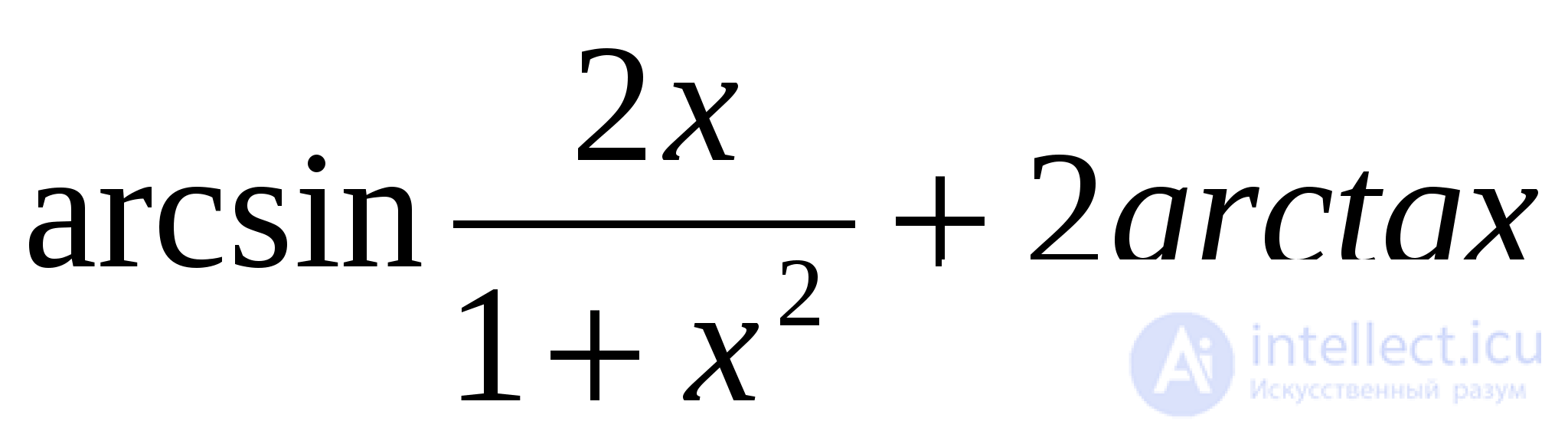 не зависит от
не зависит от 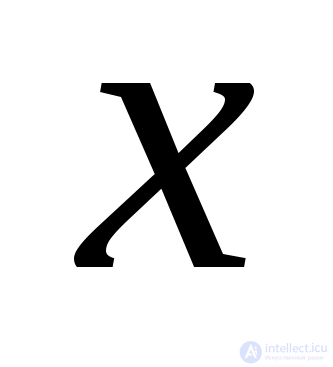 , если
, если 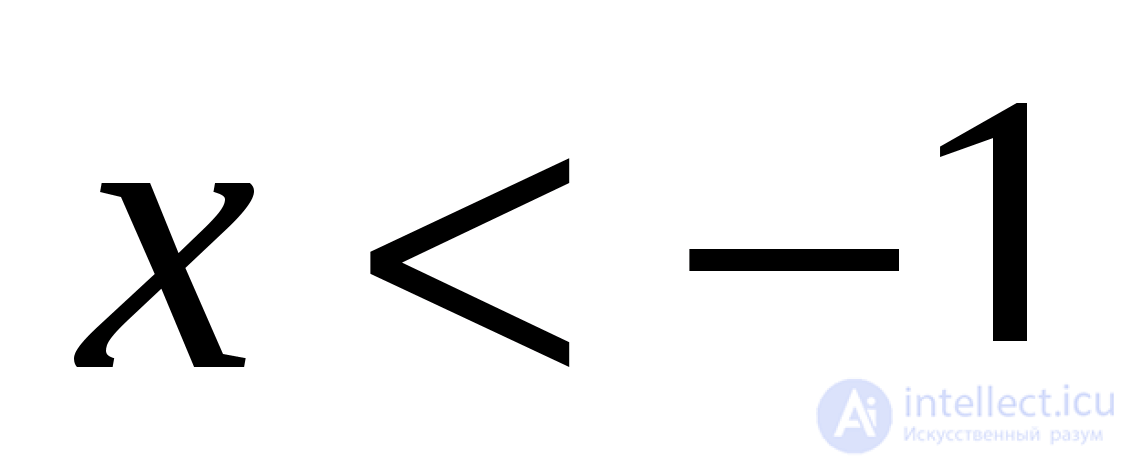 и упростите его в этом случае.
и упростите его в этом случае.
Решение: Так как 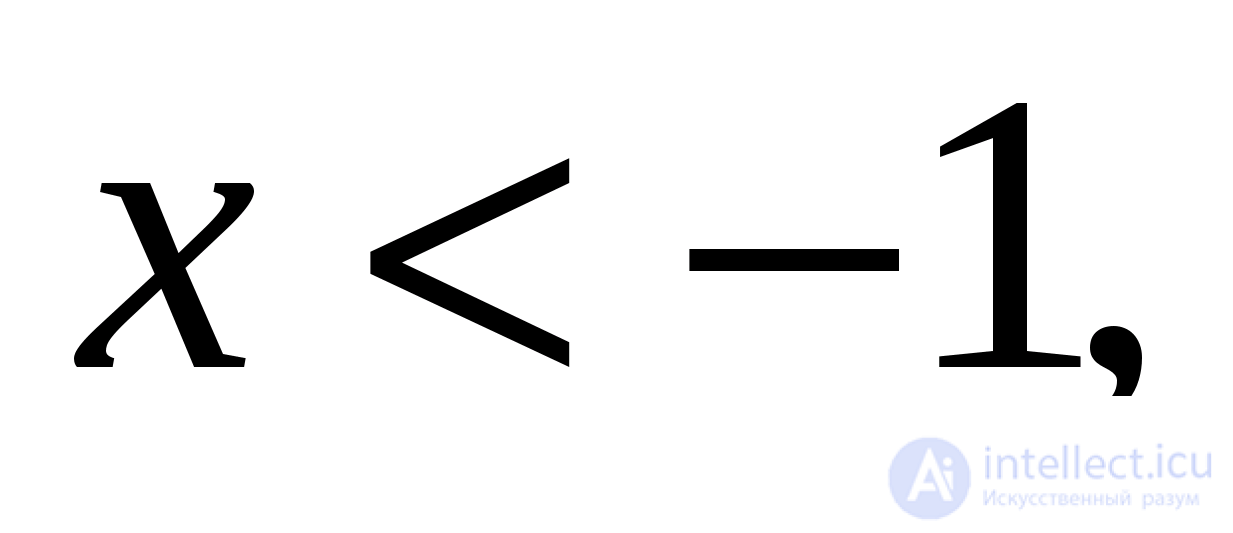 то
то 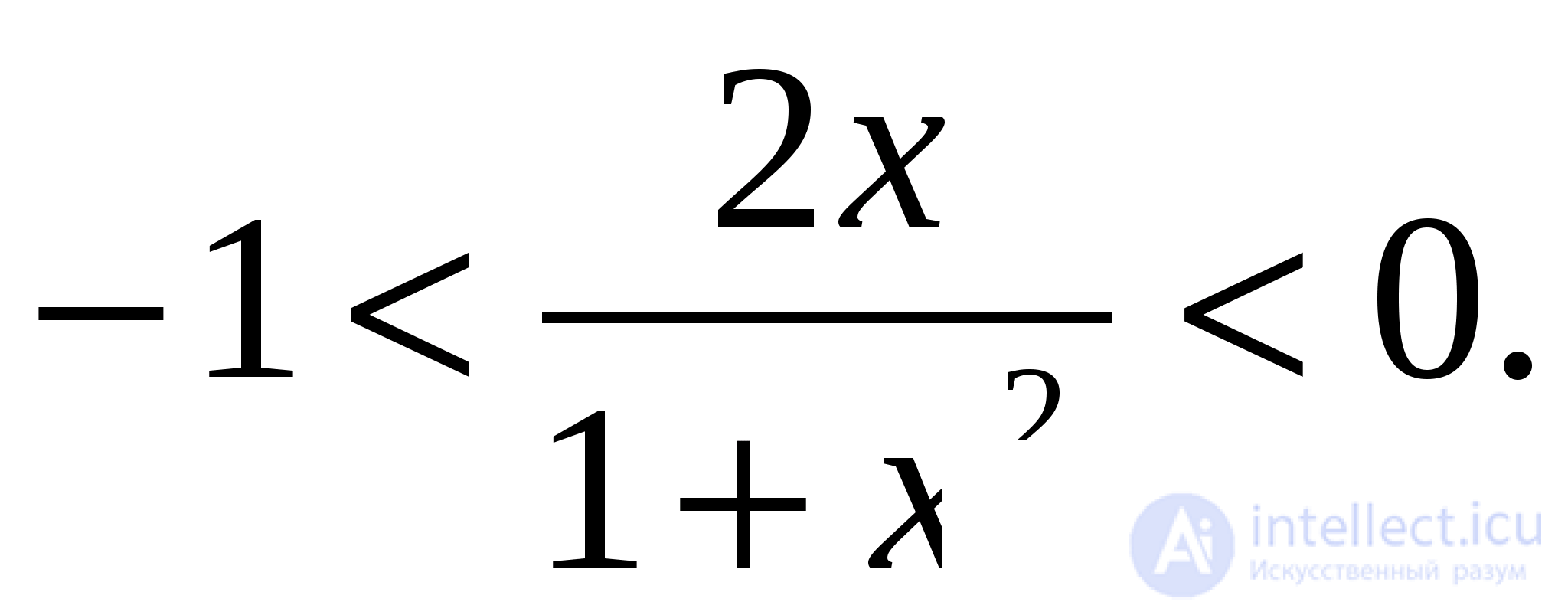 Введем обозначения
Введем обозначения

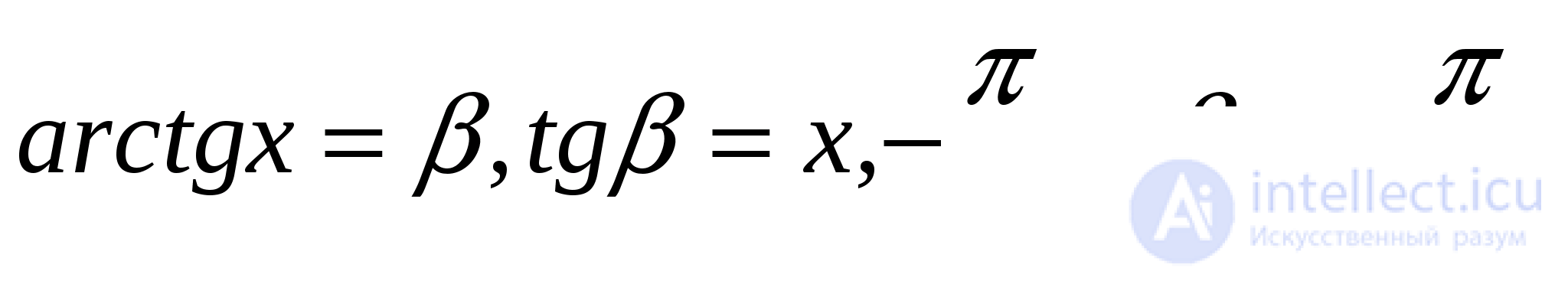 т.е.
т.е. 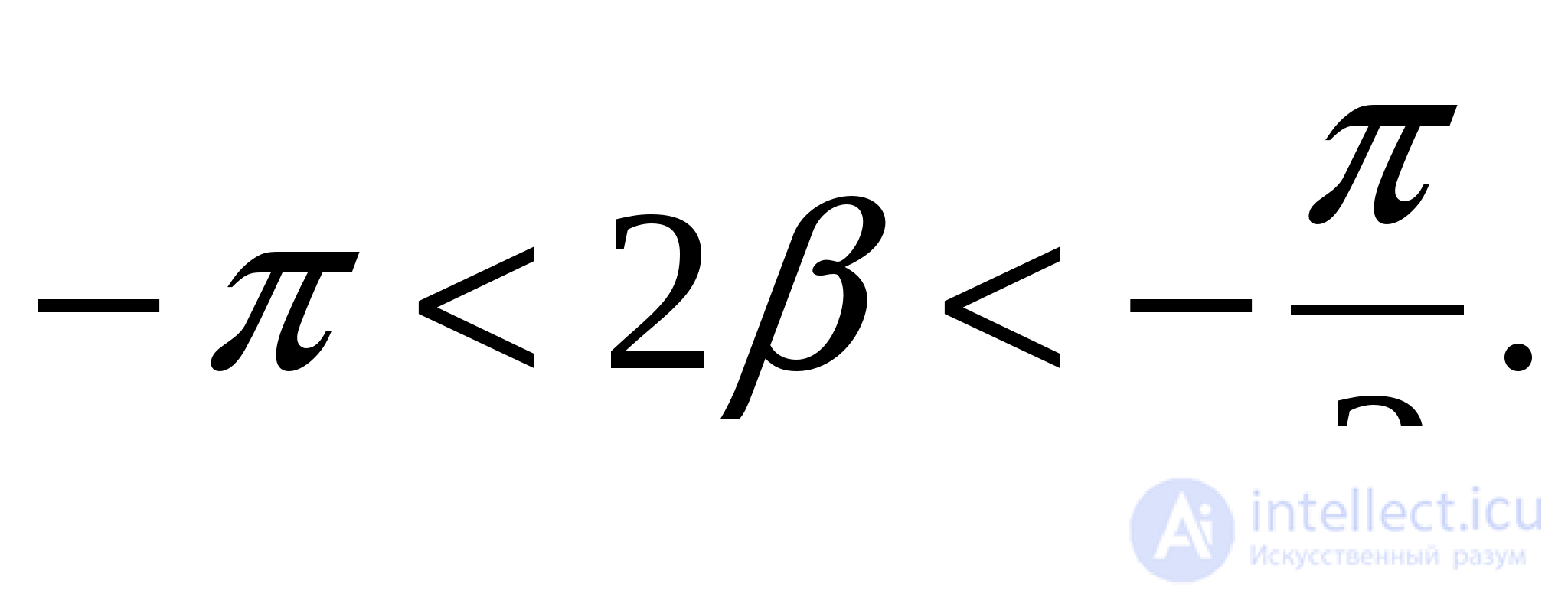
Следовательно,
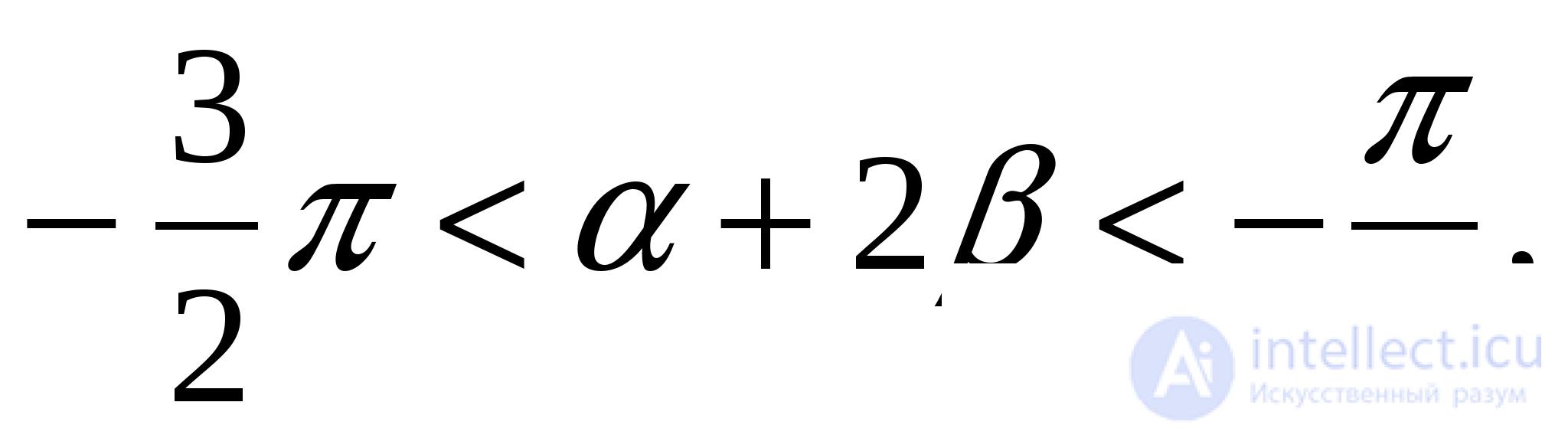
т.е. данное выражение лежит в интервале монотонности синуса. Найдем
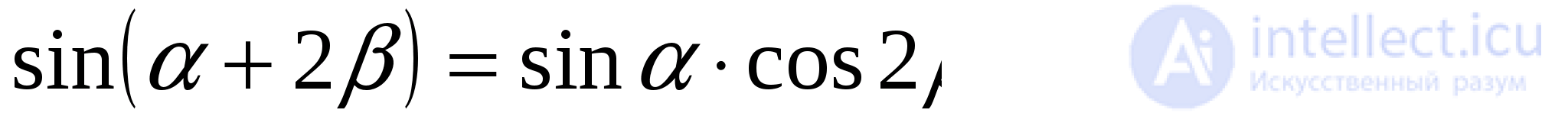

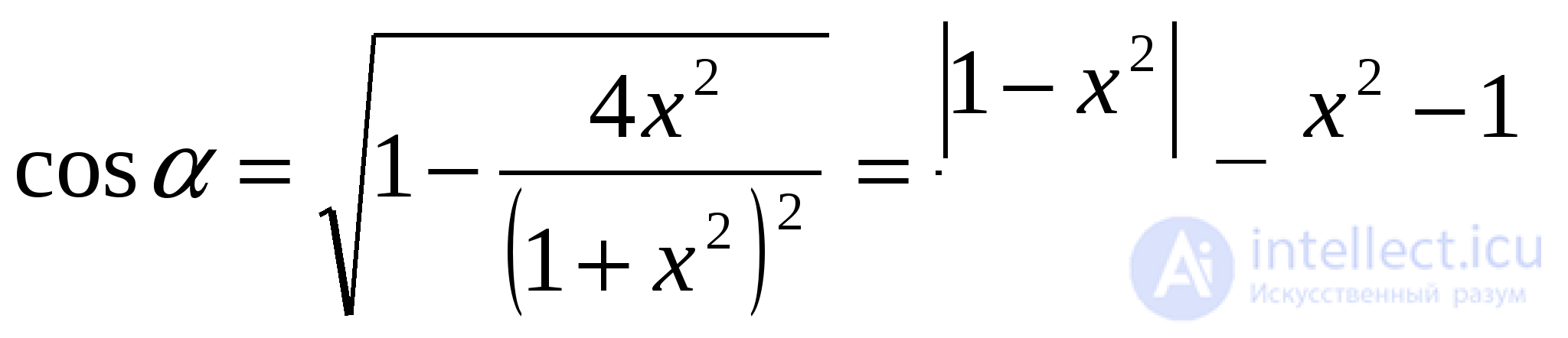 так как
так как 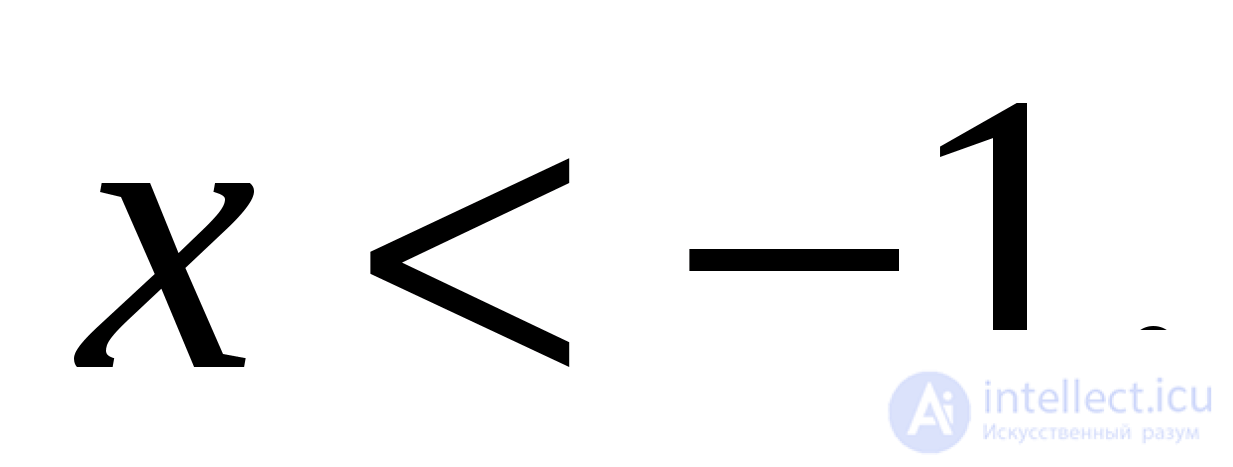
После подстановки получим
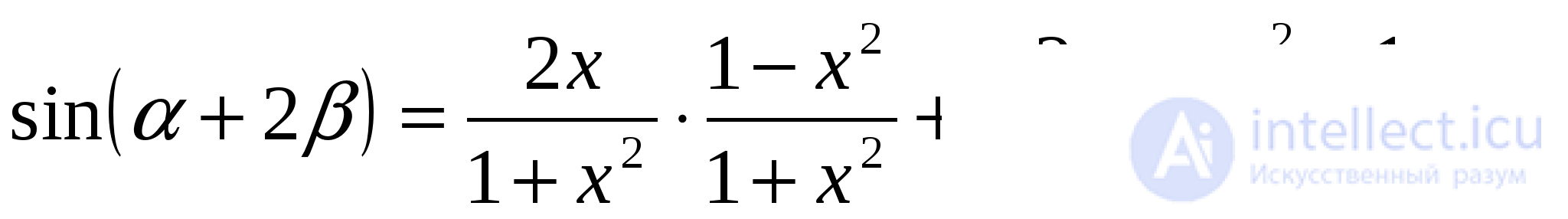
т.е. 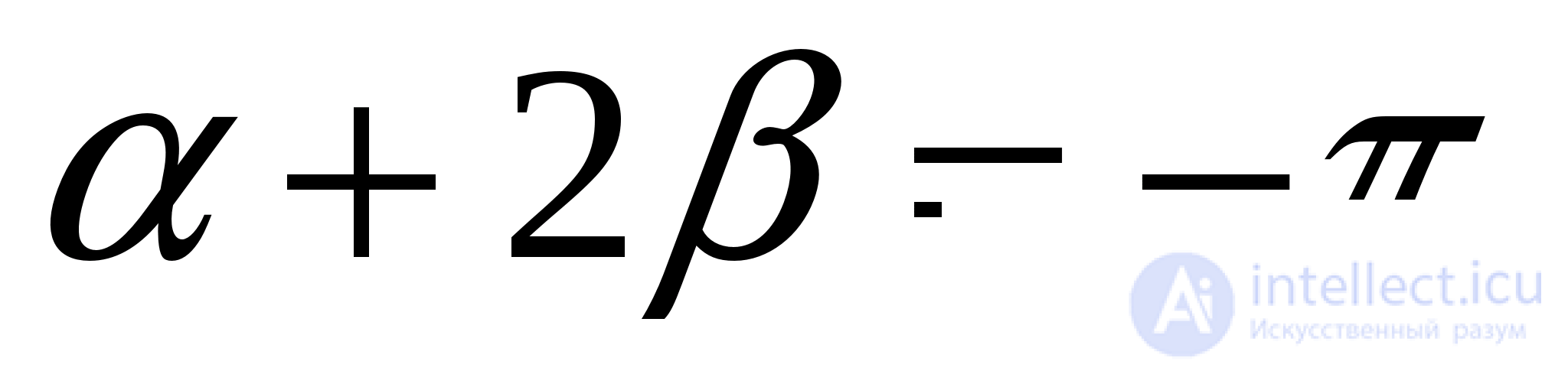
Ответ: 
Пример 4. Доказать равенство
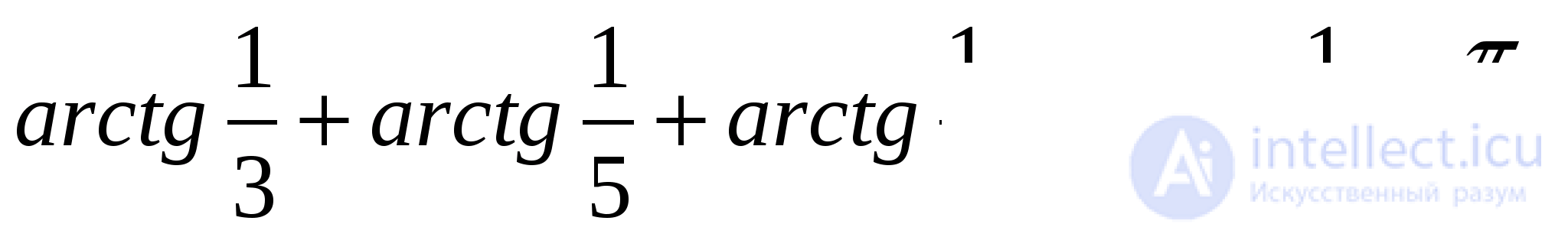
Решение: Обозначим слагаемое левой части через Имеем

Поскольку 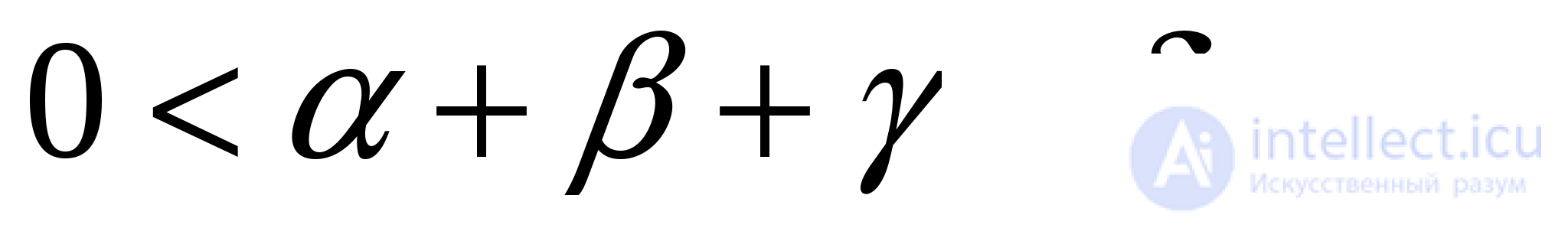 то
то 
Пример 5. Доказать равенство
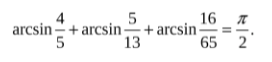
Решение: Обозначим слагаемое левой части через α, β, γ Имеем
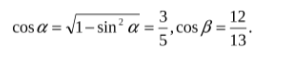
Далее, 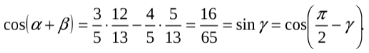
Учитывая, что - острые углы, сделаем вывод, что 
Исследование, описанное в статье про обратные тригонометрические функции, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое обратные тригонометрические функции, арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Комментарии
Оставить комментарий
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Термины: СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА