Привет, сегодня поговорим про тригонометрическая форма записи комплексного числа, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
тригонометрическая форма записи комплексного числа , настоятельно рекомендую прочитать все из категории Алгебра.
. Об этом говорит сайт https://intellect.icu
Модуль r и аргумент φ можно рассматривать как полярные координаты a = r*cosφ, b = r*sin φ. Тогда от алгебраической записи комплексного числа можем перейти к тригонометрической:
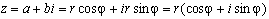
тригонометрическая форма записи комплексного числа " />
Если комплексные числа заданы в тригонометрической форме, тогда произведение и частное чисел можно найти так :

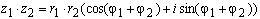
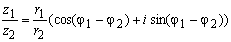

Умножение комплексных чисел имеет следующий геометрический смысл: если некоторому комплексному числу z1 = r1 (cos φ1 + isin φ1) соответствует вектор OM1, а другому комплексному числу z2 = r2 (cos φ2 + isin φ2) вектор OM2, то произведению z1 * z2 = r1 * r2 (cos(φ1 + φ2) + isin(φ1 + φ2)) соответствует вектор OM, получившийся из вектора OM1 поворотом на угол φ2 и растяжением в r2 раз при r2 ≥ 1 или сжатием в 1/r2 при 0 < r2 < 1.
Операция деления комплексных чисел также может быть интерпретирована геометрически как сочетание операций поворота и сжатия: пусть теперь комплексному числу z1 = r1 (cos φ1 + isin φ1) соответствует вектор OM1, а другому комплексному числу z2 = r2 (cos φ2 + isin φ2) вектор OM2, тогда можно утверждать, что частному от деления z1/z2 соответствует вектор OM, получившийся из вектора OM1 поворотом на угол φ2 в отрицательном направлении и сжатием в r2 раз при r2 ≥1 или растяжением в 1/r2 при 0 < r2 < 1.
Я что-то не договорил про тригонометрическая форма записи комплексного числа, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое тригонометрическая форма записи комплексного числа
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгебра
Из статьи мы узнали кратко, но содержательно про тригонометрическая форма записи комплексного числа
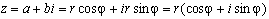 тригонометрическая форма записи комплексного числа " />
тригонометрическая форма записи комплексного числа " /> 
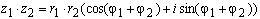
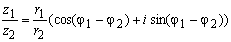

Комментарии
Оставить комментарий
Алгебра
Термины: Алгебра