Привет, сегодня поговорим про комплексная плоскость, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
комплексная плоскость , настоятельно рекомендую прочитать все из категории Алгебра.
комплексная плоскость " />
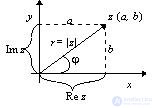
Рассмотрим декартову систему координат x0y. Пусть каждому числу z = a + bi ставится в соответствие точка z (a; b) . Такую плоскость назовем комплексной. Иными словами с каждой точкой z этой плоскости связывают радиус-вектор, определяющий положение данной точки. Угол между положительным направлением оси 0х и радиус-вектором, отсчитанным в направлении против часовой стрелки, называется аргументом.
Ось 0х называется действительной осью комплексной плоскости.
Ось 0y называется мнимой осью комплексной плоскости.
Аргумент может принимать значения из интервала -∞ < arg z < ∞. Об этом говорит сайт https://intellect.icu . Наименьшее по модулю значение аргумента называется главным и обозначается arg z = φ .
Из рисунка следует, что:
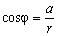
,
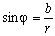
,
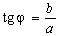
Чтобы найти аргумент, необходимо учитывать, в какой четверти комплексной плоскости находится число:
- I квадрант φ1 = arg z1 = φ;
- II квадрант φ1 = arg z1 = π - φ;
- III квадрант φ1 = arg z1 = π + φ;
- IV квадрант φ1 = arg z1 = 2π - φ; .
Найдем модуль и аргумент комплексного числа :
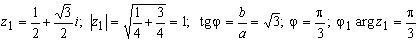
так как z1 ∈ I квадранту.
Я что-то не договорил про комплексная плоскость, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое комплексная плоскость
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгебра
Из статьи мы узнали кратко, но содержательно про комплексная плоскость
 комплексная плоскость " />
комплексная плоскость " /> 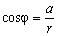 ,
, 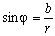 ,
, 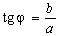
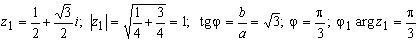
Комментарии
Оставить комментарий
Алгебра
Термины: Алгебра