Лекция
Привет, Вы узнаете о том , что такое амплитудно-фазовая характеристика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое амплитудно-фазовая характеристика, частотная характеристика, логарифмическая характеристика, логарифмическая частотная характеристика, ачф, фчф, лчх, ачх, лах, лфх, лачх, лфчх , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Частотные характеристики описывают передаточные свойства звеньев (элементов) и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием.
Зависимость отношения амплитуд выходного и входного сигналов от частоты называется амплитудной частотной характеристикой ( ачх ).
Ее обозначают А(w) (рис. 5.1).
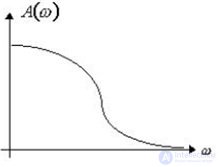
Рис.5.1. Амплитудная частотная характеристика
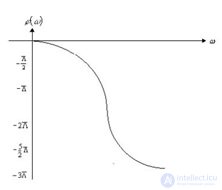
Рис. 5.2. Фазовая частотная характеристика
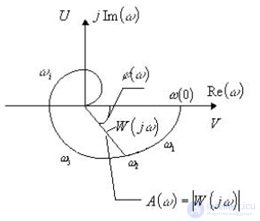
Рис. 5.3. Амплитудно-фазовая характеристика
Зависимость фазового сдвига от частоты называется фазовой частотной характеристикой (ФЧХ), и она обозначается j(w) (рис.5.2). АЧХ показывает, как хорошо пропускает элемент сигналы различной частоты. ФЧХ показывает, какое отставание или опережение входного сигнала по фазе создает элемент при различных частотах.
Амплитудную частотную и фазовую частотную характеристики можно объединить в одну общую: амплитудно-фазовую частотную характеристику (АФЧХ) или (АФХ) (рис.5.3). Она обозначается W(jw) и представляет собой функцию комплексного переменного , модуль которой равен А(w), а аргумент равен j(w).
Каждому фиксированному значению частоты wi соответствует комплексное число W(jwi), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(wi) и угол поворота j(wi) (см. рис. 5.3.1). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.

Рис 5.3.1
АФХ W(jw), как и любая комплексная величина, может быть представлена в показательной:
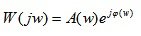 (5.1)
(5.1)
или в алгебраической форме:
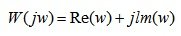 (5.2)
(5.2)
где Re(w) – проекция вектора W(jw) на вещественную ось, а lm(w) – проекция вектора W(jw) на мнимую ось.
Re(w) называется вещественной частотной характеристикой, а lm(w) – мнимой частотной характеристикой.
АФХ есть изображение по Фурье импульсной переходной функции:
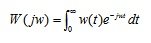 (5.3)
(5.3)
Обратное преобразование Фурье АФХ даст импульсную переходную функцию:
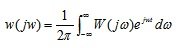 (5.4)
(5.4)
Аналитическое выражение для АФХ конкретного элемента можно получить из его передаточной функции подстановкой p=jw :
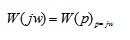 (5.5)
(5.5)
Наиболее общей является амплитудно-фазовая частотная характеристика (АФЧХ), которая формально определяется из передаточной функции заменой p на аргумент jw.
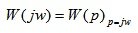 (5.6)
(5.6)
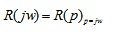 (5.7)
(5.7)
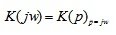 (5.8)
(5.8)
Часто W(jw), R(jw), K(jw) называют комплексным коэффициентом передачи.
Амплитудно-фазовая частотная характеристика является функцией комплексной переменной jw и может быть выражена через модуль и фазу. Например, для АФЧХ звена K(jw) модуль будет K(jw)=K(p) фаза (p(w)=argK(jw)). АФЧХ может быть выражена в следующих формах:
- алгебраическая форма:
K(jw)=P(jw)+jQ(w), (5.9)
где P(jw) – вещественная часть , jQ(w) – мнимая часть;
- показательная форма:
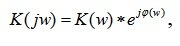 (5.10)
(5.10)
где:
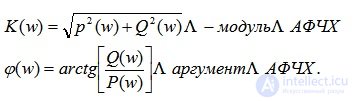
В равенстве
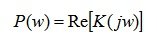 (5.11)
(5.11)
вещественная часть комплексной функции K(jw), называемая вещественной частотной характеристикой (ВЧХ);
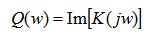 - мнимая часть комплексной функции K(jw) называемая мнимой частотной характеристикой (МЧХ).
- мнимая часть комплексной функции K(jw) называемая мнимой частотной характеристикой (МЧХ).
В равенстве
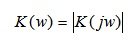 (5.12)
(5.12)
модуль комплексной функции K(jw) называемый амплитудно-частотной характеристикой (АЧХ). Амплитудно-частотная характеристика АФЧХ представляет собой зависимость коэффициента усиления системы от частоты входного гармонического сигнала:
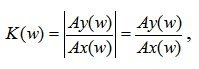 (5.13)
(5.13)
где Ay(w) – выходной сигнал; Ax(w) – входной сигнал.
Следовательно, АЧХ равна отношению амплитуд вынужденной составляющей выходного и входного сигналов.
В равенстве (5.12) 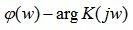 - аргумент комплексной функции K(jw), называемой фазовой частотной характеристикой (ФЧХ).
- аргумент комплексной функции K(jw), называемой фазовой частотной характеристикой (ФЧХ).
Следовательно, ФЧХ равна разности фаз вынужденной составляющей выходного и входного сигналов.
Амплитудная K(w) и фазовая частотные ?(w) характеристики определяют вынужденную составляющую выходного сигнала системы при воздействии на нее гармонического входного сигнала, заданного в скалярном виде. Об этом говорит сайт https://intellect.icu . Так, если на систему действует гармонический входной сигнал x(t) вида , то вынужденная составляющая выходного сигнала определяется соответственно 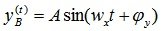 , где
, где
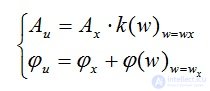 (5.14)
(5.14)
Годографом частотной характеристики K(jw) называют траектории точки K(jw) на комплексной плоскости при изменении частоты w от 0 до ? . Точка годографа, соответствующая w=0, называется началом годографа, а точка соответствующая w=? конечной точкой.
Построение годографа производится по парам вещественных характеристик. P(w), Q(w) или K(w), ?(w).
При практических расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (логарифмические частотные характеристики – лчх ). Они характеризуются большей линейностью и на определенных участках изменения частот могут быть заменены прямыми линиями и в целом представлены ломаными линиями. Причем отрезки прямых в большинстве случаев можно построить при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, т.к. умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.
За единицу длины по оси частот ЛЧХ принимается декада. Декада– интервал частот, заключенный между произвольным значением и его десятикратным значением. Отрезок, соответствующий одной декаде, равен 1.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику ( лачх )
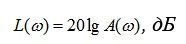 (5.15)
(5.15)
ординаты которой измеряют в логарифмических единицах - бе лах или децибелах (0,1 бела), сокращенно дБ (рис. 5.4).
Бел– единица измерения отношения мощности двух сигналов. Если мощность одного сигнала больше мощности другого в 10 раз, то эти мощности отличаются на 1 Б (lg10 = 1).
Т.к. мощность сигнала пропорциональна квадрату амплитуды, то
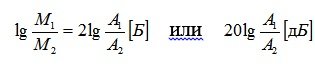
При построении фазовой частотной характеристики логарифмический масштаб применяется только для оси абсцисс.
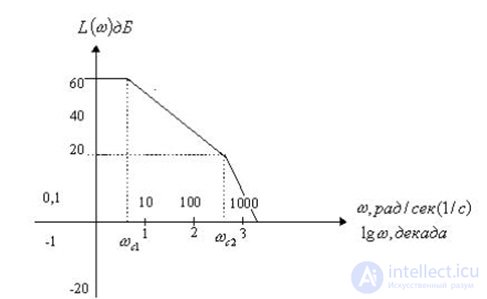
Рис. 5.4. Логарифмическая амплитудно-частотная характеристика
Формулы для расчетов
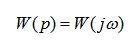 (5.16)
(5.16)
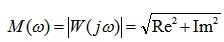 (5.17)
(5.17)
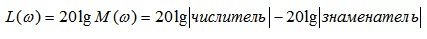 (5.18)
(5.18)
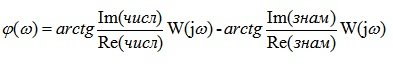 (5.19)
(5.19)
Пример 1. Передаточная функция разомкнутой системы имеет вид:
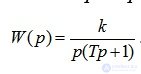 .
.
Определить частотные характеристики.
Решение:
АФХ определяем по формуле 5.16:
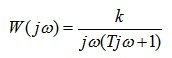
АЧХ определяем по формуле 5.17:
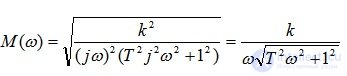
ЛАХ определяем по формуле 5.18:
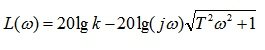
лфх определяем по формуле 5.19:
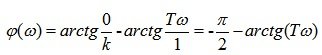
Пример 2. Передаточная функция системы имеет вид:
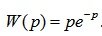 . Определить частотные характеристики.
. Определить частотные характеристики.
Решение:
АФХ: 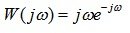
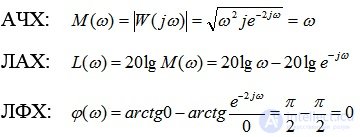
Пример 3. Построить график ЛАХ асимптотически (приближено) для функции
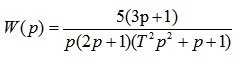
Решение:
Параметры системы:
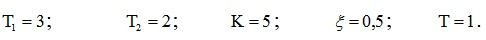
Заменив p на jw, получим:
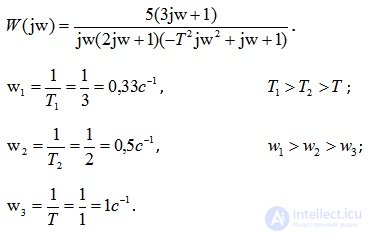
Построение ЛАХ всегда начинается с идеально-интегрирующего звена, которое дает отрицательный угол наклона прямой – 20 дБ/декаду. В диапазоне частот от w1 до w2 график ЛАХ будет представлять собой прямую с нулевым углом наклона, так как на этом интервале включается форсирующее звено (3p+1), которое дает угол наклона +20дБ/декаду, что в сочетании с идеально-интегрирующим звеном дает нулевой угол наклона прямой. В диапазоне частот от w2 до w3график будет представлять собой прямую с отрицательным наклоном -20дБ/декаду, так как подключается апериодическое звено 1-го порядка. В диапазоне частот от w3 до ? график ЛАХ примет вид прямой с отрицательным наклоном -60дБ/декаду, так как в этом диапазоне частот подключается колебательное звено, дающее отрицательный наклон прямой -40дБ/декаду.
Результат построения ЛАХ представлен на рис. 5.5.
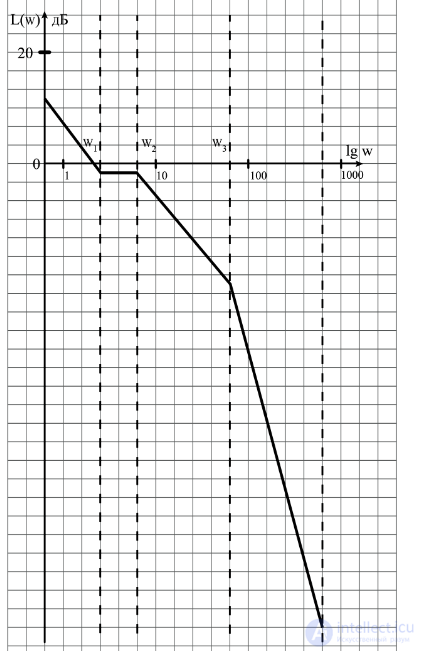
Рис.5.5. Асимптотическое построение ЛАХ

1. Для звеньев или соединений звеньев, заданных передаточными функциями:
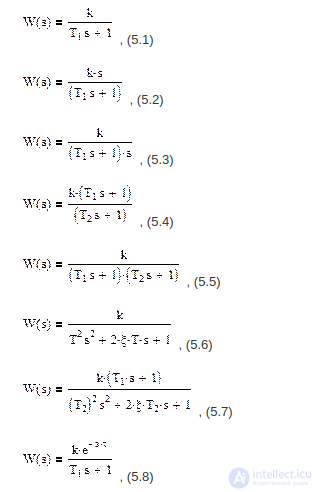
построить АФЧХ, АЧХ, ФЧХ, ЛАХ при различных значениях параметров.
2. Для заданной преподавателем передаточной функции промоделировать прохождение через исследуемый объект гармонического сигнала с различной частотой
Теоретические сведения
Амплитудно-фазовой (частотной) характеристикой (АФЧХ) называется функция W(jw), определяющая изменение амплитуды и фазы выходной величины системы или ее отдельного элемента в установившемся режиме при приложении на входе гармонического воздействия. АФЧХ можно определить как преобразование Фурье весовой функции объекта или системы:
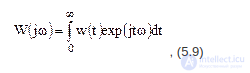
либо формальным переходом от передаточной функции W(s) при замене s на jw. Для  - многочлены m-й и n-й степеней от s, частотная характеристика будет равна
- многочлены m-й и n-й степеней от s, частотная характеристика будет равна
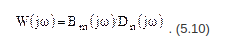
Освобождаясь от мнимого числа в знаменателе, путем домножения на комплексно сопряженную знаменателю функцию 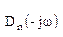 получаем
получаем
,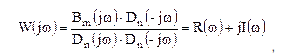
где R(w), I(w) – вещественная и мнимая части частотной функции системы.
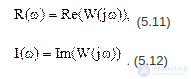
Представляя комплексные функции числителя и знаменателя (5.10) в показательной форме, можно записать:
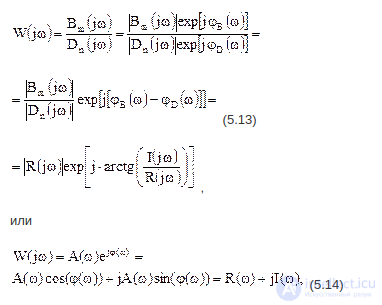
где  – модули комплексных функций числителя и знаменателя частотной характеристики,
– модули комплексных функций числителя и знаменателя частотной характеристики,
jB(w),jD(w) – соответственно фазы комплексных функций числителя и знаменателя,
А(w) – амплитудно-частотная характеристика (АЧХ), равная
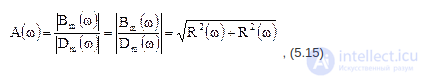
j(w) – фазовая частотная характеристика (ФЧХ),
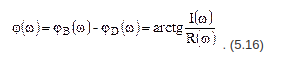
Если рассматривать прохождение гармонического сигнала через линейный объект, то при сохраняющейся частоте сигнала амплитудно-частотная характеристика также определяется как зависимость отношения амплитуды выходного гармонического сигнала в установившемся режиме к амплитуде входного сигнала от частоты сигнала. Соответственно, фазовая частотная характеристика есть зависимость смещения по фазе выходного гармонического сигнала относительно входного от частоты сигнала.
В MathCad для выделения значения фазы предусмотрена функция arg():
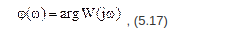
либо функция atan, определяющие значения фазы только в пределах от -p до +p. Если фаза выходит за пределы (-p,+p), ее необходимо скорректировать с учетом знаков действительной и мнимой частей АФЧХ.
Графически амплитудно-фазовая частотная характеристика изображается на комплексной плоскости в полярных координатах (А, j) как годограф функции W(jw). Можно построить амплитудно-частотную характеристику и в прямоугольных координатах (Im[W(jw)], Re[W(jw)]). При этом частоту w изменяют от 0 до ¥.
Логарифмические частотные характеристикииспользуются при исследовании систем автоматического управления с помощью частотных методов и представляют собой логарифмическую амплитудную и логарифмическую фазовую характеристики.
Логарифмической амплитудной частотной характеристикой (ЛАХ) называется кривая, соответствующая 20 десятичным логарифмам модуля частотной характеристики системы, построенная в логарифмической координатной сетке: логарифм амплитуды – логарифм частоты (или частота, отложенная в декадах):

При построении логарифмической амплитудной характеристики по оси ординат откладывают величину L(θ) , единицей измерения для которой является децибел. По оси абсцисс – логарифм частоты q. Равномерной единицей на оси абсцисс является декада – отрезок, на котором значение частоты увеличивается в 10 раз. Точка пересечения ЛАХ с осью абсцисс называется частотой среза wс.
Значению А(w)= 1 исходя из (5.18) соответствует L(θ)=0 , в этом случае ЛАХ проходит по оси абсцисс. Верхняя полуплоскость ЛАХ соответствует значениям А(w) > 1 (усиление амплитуды), а нижняя полуплоскость – значениям А(w) < 1 (ослабление амплитуды).
При построении логарифмической фазовой характеристики (ЛФХ) отсчет углов j(w) идет по оси ординат в обычном масштабе в радианах либо градусах, а по оси абсцисс откладывается логарифм частоты q или частота в декадах.
Логарифмические частотные характеристики удобны для анализа систем, образованных последовательным соединением элементарных звеньев (рис. 5.1), поскольку позволяют перейти от операции умножения модулей частотных характеристик элементарных звеньев к операции сложения их логарифмических амплитудных характеристик, что иллюстрируется следующими зависимостями:

В MathCad комплексные вычисления производятся с помощью символьного процессора. Для выполнения операций над комплексными числами мнимую единицу j необходимо заранее задать как  , либо использовать стандартную мнимую переменную i коэффициентом 1
, либо использовать стандартную мнимую переменную i коэффициентом 1  . По окончании редактирования формулы запись приобретает вид: i.
. По окончании редактирования формулы запись приобретает вид: i.
Запишем частотную передаточную функцию апериодического звена первого порядка:
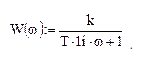
При выходе из редактирования (щелчок мыши в свободном поле документа) формула приобретет вид:
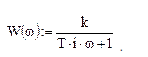 .
.
Выделим действительную и мнимую части амплитудно-фазовой частотной характеристики, используя функцию complex, которую можно выбрать в панели инструментов «Математика» в меню «Символы»:
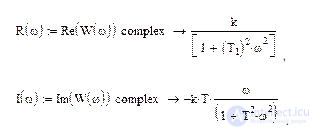
Для построения графиков частотных характеристик необходимо задать диапазон изменения частоты, например, ω := 0,0 2..100 , коэффициент усиления k:=0.75 и постоянную времени T:=0.5 .
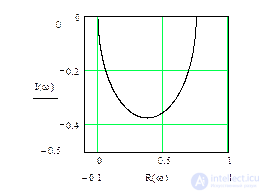
Рис.5.2. Комплексная частотная характеристика
Амплитудная частотная характеристика рассчитывается следующим образом:
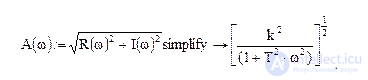 .
.
Использование функции simplify позволяет упростить результат вычислений. Однако последняя запись, полученная с помощью MathCad, может быть представлена в более удобном виде: 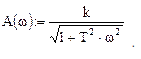 .
.
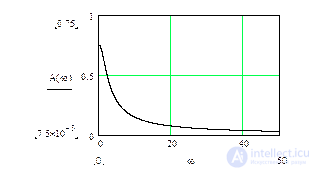
График АЧХ показан ниже.
Рис.5.3. Амплитудная частотная характеристика
Фазовую частотную характеристику определим с помощью функции atan
.
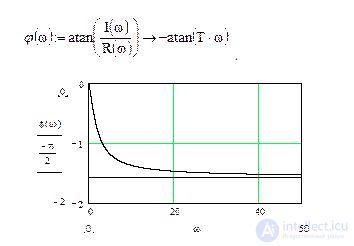
Рис.5.4. Фазовая частотная характеристика
Логарифмическая амплитудная характеристика рассчитывается как
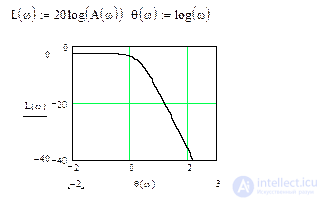
Рис.5.5. Логарифмическая амплитудная частотная характеристика
При построении асимптотической ЛАХ, представляющей собой кусочно-линейную функцию, можно воспользоваться программным модулем (панель "Инструменты программирования"). Для передаточной функции апериодического звена первого порядка асимптотическая ЛАХ может быть построена по программе:
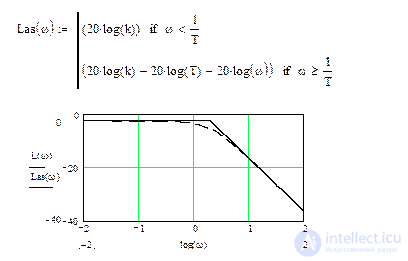
Рис.5.6. Асимптотическая ЛАХ
Моделирование прохождения гармонического сигнала через линейную систему осуществляется путем решения дифференциального уравнения с гармонической правой частью
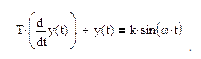 .
.
Преобразование Лапласа от входного гармонического сигнала x(t)=sin(t) :
. 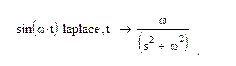
Выходной сигнал y(s) в преобразованиях Лапласа имеет вид:
.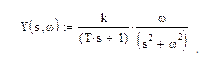
Выполняем обратные преобразования Лапласа и записываем выходной сигнал:
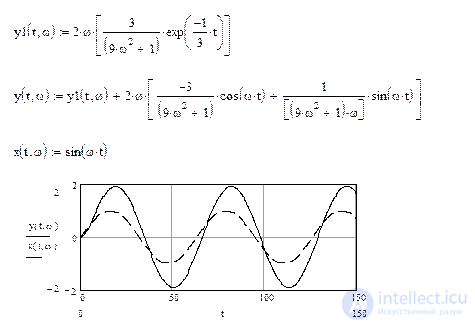
Рис.5.7. Сигналы на входе и выходе звена для w=0.1
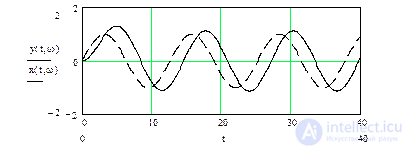
Рис.5.8. Сигналы на входе и выходе звена для w=0.5
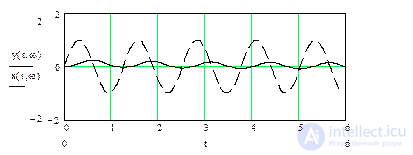
Рис.5.9. Сигналы на входе и выходе звена для w=5
Как видно из рисунков, при постоянной амплитуде входного гармонического сигнала, амплитуда сигнала на выходе апериодического звена с возрастанием частоты существенно уменьшилась, а смещение сигналов по фазе приблизилось к p/2. Апериодическое звено работает как фильтр высоких частот.
Прочтение данной статьи про амплитудно-фазовая характеристика позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое амплитудно-фазовая характеристика, частотная характеристика, логарифмическая характеристика, логарифмическая частотная характеристика, ачф, фчф, лчх, ачх, лах, лфх, лачх, лфчх и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления