Лекция
Привет, Вы узнаете о том , что такое определение параметров динамических характеристик линейных звеньев систем автоматического управления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое определение параметров динамических характеристик линейных звеньев систем автоматического управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Цель работы – аналитическое и имитационное исследование динамических характеристик моделей линейных звеньев систем автоматического управления (САУ) и определение их параметров по переходным и частотным характеристикам.
| № в. | Название звена | Передаточная функция звена |
| Интегрирующее |  |
|
| Дифференцирующее |  |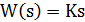
|
| Усилительное (безынерционное) |  |
|
| Апериодическое 1-го порядка (инерционное) |  |
|
| Апериодическое 2-го порядка (все корни вещественные) |  |
|
| Колебательное |  |
|
| Консервативное |  |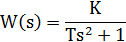
|
| Интегрирующее с запаздыванием (реальное интегрирующее) |  |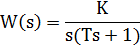
|
| Дифференцирующее с запаздыванием (реальное дифференцирующее) |  |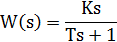
|
| Форсирующее |  |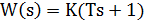
|
| Изодромное |  |
Часто используется описание колебательного звена в виде:
Временные характеристики динамического звена представляют собой зависимость выходного сигнала системы от времени при подаче на ее вход некоторого типового воздействия. Обычно выполняется анализ выхода системы на единичный скачок (функция Хевисайда)и импульсную функцию (функция Дирака или -функция).
Единичный скачок 1(t) определяется условиями:
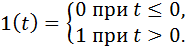
Реакция САУ на единичный скачок называется переходной функцией системы и обозначается h(t). При неединичном ступенчатом воздействии g(t)=N1(t), гдеN= const, в соответствии с принципом суперпозиции выходная реакция системы будет
y(t)=Nh(t) .
Импульсная функция 
определяется условиями:
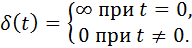
Очевидно:
Реакция САУ на импульсную функцию называется импульсной переходной функцией системы (функцией веса) и обозначается w(t). Импульсная и переходная функции системы связаны соотношением
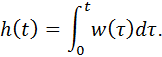
В пакете MatLab имеется два основных варианта для исследования передаточных функций и моделирования САУ:
– использование команд пакета расширения Control SystemToolbox;
– использование пакета Simulink.
Control System Toolbox [8, 9] предназначен для работы с LTI-моделями (Linear Time Invariant Models – линейные модели с постоянными параметрами) систем управления.
Команда, создающая LTI-систему c одним входом и одним выходом в виде передаточной функции, имеет следующий синтаксис:
где 
и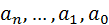 
- значения коэффициентов полиномов В и А в (3).
Например, если требуется описать ПФ вида:
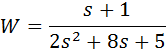
и узнать значения ее нулей и полюсов, то нужно ввести в окне команд MatLab следующие команды:
>> w=tf([1 1],[2 8 5])>> zero(w)
>> pole(w)
Исследовать реакцию LTI-модели на типовые входные воздействияможно с помощью команд
>> step(w)>> impulse(w)
Можно получить на одном графике реакцию сразу нескольких динамических звеньев, если использовать команды вида:
>> step(w,w1,w2)
>> impulse(w, w1,w2)
В приведенных примерах время моделирования выбирается автоматически. Об этом говорит сайт https://intellect.icu . При необходимости его можно явно указать в команде
>> step(w, w1, w2, t),
где t – время моделирования в секундах.
На рис. 1 показан пример моделирования динамики колебательного звена при различных параметрах:
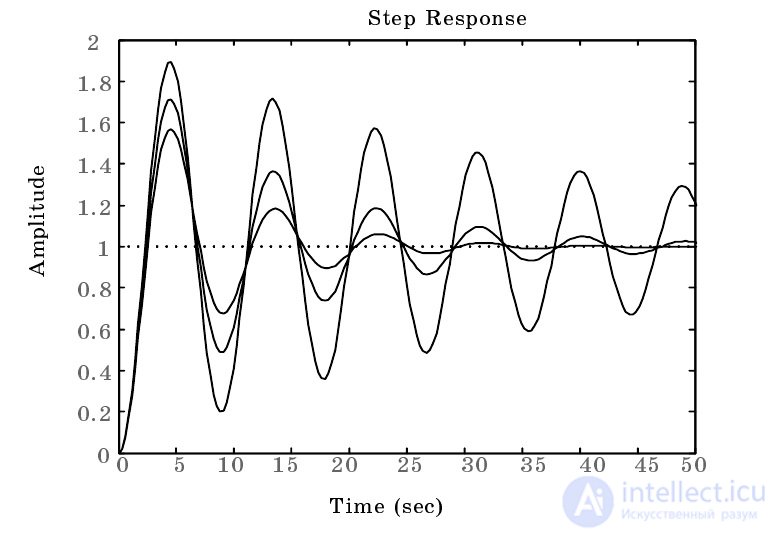
Рис. 1. Исследование реакции колебательного звена
>>w=tf([1],[2 0.3 1]);
>> w1=tf([1],[2 0.5 1]);
>> w2=tf([1],[2 0.1 1]);
>> step(w,w1,w2,50).
В Simulink MatLab ПФ можно описать с помощью блока Transferfcn в разделе библиотеки Continuous. Для подачи типовых воздействий надо использовать блок Step из раздела Sources. Импульсную переходную характеристику звена можно получить, подавая на вход импульс маленькой длительности и большой амплитуды (приближение функции) при нулевых начальных условиях.
Для наглядного представления сложной системы как совокупности элементов и связей между ними используются структурные схемы.
Структурной схемой называется схема САУ, изображенная в виде соединения ПФ составляющих ее звеньев.
Структурная схема показывает строение автоматической системы, наличие внешних воздействий и точки их приложения, пути распространения воздействий и выходную величину. Динамическое или статическое звено изображается прямоугольником, в котором указывается ПФ звена или ее математическое выражение. Воздействия на систему и влияние звеньев друг на друга (сигналы) изображаются стрелками. В каждом звене воздействие передается только от входа звена к его выходу.
На динамическое звено может воздействовать лишь одна входная величина, поэтому используются блоки суммирования и сравнения сигналов. Суммироваться и сравниваться могут лишь сигналы одной и той же физической природы.
Структурная схема может быть составлена по уравнению системы в пространстве состояний или по дифференциальным уравнениям системы. При составлении структурной схемы удобно начинать с изображения задающего воздействия и располагать динамические звенья, составляющие прямую цепь системы, слева направо до регулируемой величины. Тогда основная обратная связь и местные обратные связи будут направлены справа налево.
Различные способы преобразования структурных схем облегчают определение ПФ сложных САУ и дают возможность привести многоконтурную систему к эквивалентной ей одноконтурной схеме.
Преобразование структурной схемы должно осуществляться на основании правил. Правила преобразования структурных схем можно найти в справочной литературе [1, 2], основные из них приведены в табл. 2.1.
Таблица 2.1
| Преобразование | Структурная схема | |
| Исходная | Эквивалентная | |
| Свертывание последовательного соединения |  |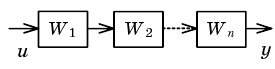
 |
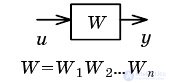| Свертывание параллельного соединения |  |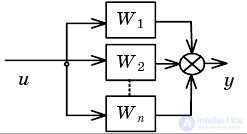
 |
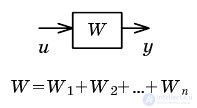| Свертывание обратной связи |  |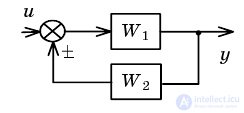
 |
| Перенос узлачерез звено вперед |  |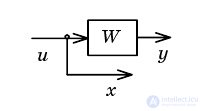
 |
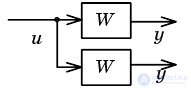
| Перенос узла через звено назад |  |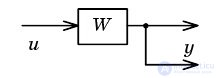
 |
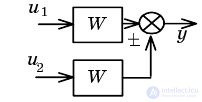
| Перенос сумматорачерез звено вперед |  |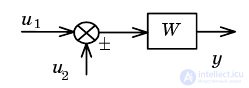
 |
| Перенос сумматорачерез звено назад |  |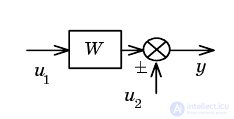
 |
| Перенос прямой связи через звено |  |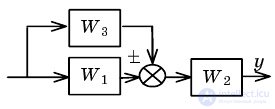
 |
| Перенос узла через сумматор |  |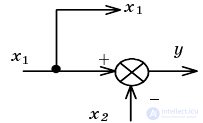
 |
| Перенос узла через сумматор назад |  |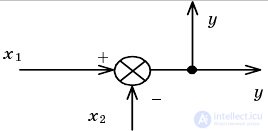
 |
Пример. Пусть необходимо получить эквивалентное представление для структуры, приведенной на рис. 2.1.
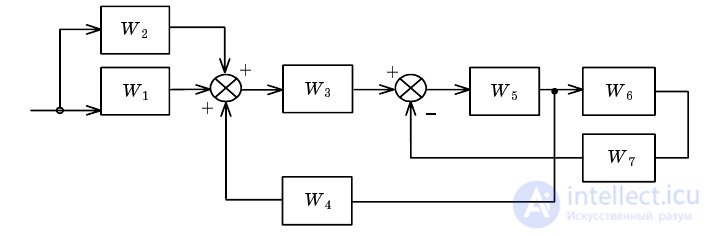
Рис. 2.1. Исходная структура САУ
Преобразование включает несколько этапов, показанных на рис.2.2-2.5.
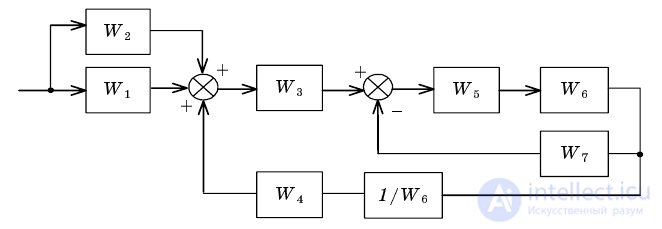
Рис. 2.2. Перенос узла через сумматор
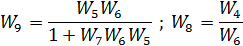
Рис. 2.3. Свертывание обратной связи и последовательного соединения
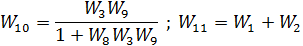
Рис. 2.4. Свертывание обратной связи и параллельного соединения
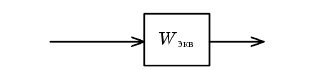
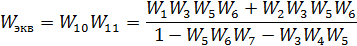
Рис. 2.5. Свертывание последовательного соединения
Таким образом, первый способ преобразования структурных схем заключается в непосредственном использовании правил, приведенных в табл.2.1. Неудобство использования этого подхода заключается в том, что порядок применения формул здесь достаточно произволен, возможны ошибочные шаги, усложняющие поиск решения.
Второй способ для получения ПФ многоконтурной системы заключается в использовании модели системы в виде сигнального графа.
Сигнальный граф позволяет графически описать линейные связи между переменными, он состоит из узлов (вершин) и соединяющих их направленных ветвей.
Ветвь соответствует блоку структурной схемы, она отражает зависимость между входной и выходной переменными. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную.
Последовательность ветвей между двумя узлами называется путем. Контуром называется замкнутый путь, который начинается и заканчивается в одном и том же узле, причем ни один узел не встречается на этом пути дважды. Коэффициент передачи контура - это произведение всех входящих в него дуг.
Контуры называются не касающимися, если они не имеют общих узлов.
Сигнальный граф однозначно соответствует структурной схеме.
Пусть X(s) и Y(s) - входная и выходная переменные системы. Тогда для вычисления ПФ системы управления по ее графу можно воспользоваться формулой Мейсона:
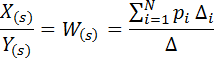
где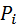 
– i-й путь от входа к выходу; N - количество путей; 
- определитель графа;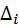 
- дополнительный множитель для пути.
Определитель графа получается по формуле:
где - 
сумма коэффициентов передачи всех отдельных контуров;
- сумма произведений всех возможных комбинаций из двух не касающихся контуров;
- сумма произведений всех возможных комбинаций из трех некасающихся контуров.
Дополнительный множитель для i-го пути равен определителю графа, в котором приравнены нулю коэффициенты передачи контуров, касающихся этого пути.
Рассмотрим пример получения ПФ многоконтурной системы с использованием формулы Мейсона для структуры рис. 1, которой соответствует граф, показанный на рис. 2.6.
От входа к выходу ведут два пути:
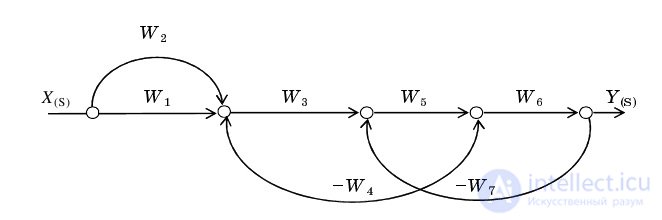
Рис. 2.6. Описание системы управления сигнальным графом
В графе есть два контура:
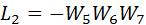
Контур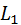 
касается контура 
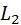, поэтому определитель графа вычисляется по формуле:
Контуры в этом примере касаются всех путей, поэтому дополнительные множители путей
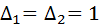
Окончательно можно записать:
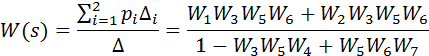
Таким образом, использование сигнальных графов и применение формулы Мейсона позволяет алгоритмизировать процесс упрощения структурной схемы.
Прочтение данной статьи про определение параметров динамических характеристик линейных звеньев систем автоматического управления позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое определение параметров динамических характеристик линейных звеньев систем автоматического управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про определение параметров динамических характеристик линейных звеньев систем автоматического управления
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления