Лекция
Привет, Вы узнаете о том , что такое законы управления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое законы управления, закон управления, пид регуляторы, математические модели сау , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
законы управления представляют собой установленные теоретическим или эмпирическим способом и логически обоснованные зависимости между целями управленческой деятельности и методами их достижения.
закон управления - это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t). Эта зависимость может быть представлена в виде
u(t) = F(x, g, f), (8.1) (обяснение ниже)
Закономерность – необходимая, существенная, постоянно повторяющаяся взаимосвязь явлений реального мира, определяющая этапы и формы процесса становления, развития явлений природы, общества и духовной культуры.
Согласно сложившейся практике законы управления принято делить на три основные группы.
К первой группе относятся общие (объективные) законы управления. Объективными законами управления принято считать законы, свойственные управлению в целом и выражающие зависимости, формирующиеся независимо от воли отдельных субъектов.
Во вторую группу входят частные, или субъективные, законы управления, посредством применения которых можно в значительной степени повысить эффективность функционирования системы управления в целом, а также ее отдельных элементов и звеньев. К числу субъективных законов управления принадлежат закон изменения функций управления, закон сокращения числа ступеней управления, закон распространенности контроля.
И наконец, к третьей группе целесообразно отнести законы, не связанные непосредственно с управлением, но способные оказать значительное влияние на результаты деятельности организации. К законам третьей группы относятся экономические, юридические, социальные и иные законы. Такие законы можно обозначить термином "специальные".
Предположим, что структурная схема такой САУ состоит из некоторого числа элементов (звеньев). Группируя звенья по функциональному принципу (что звенья делают), структурную схему САУ можно привести к следующему типовому виду:
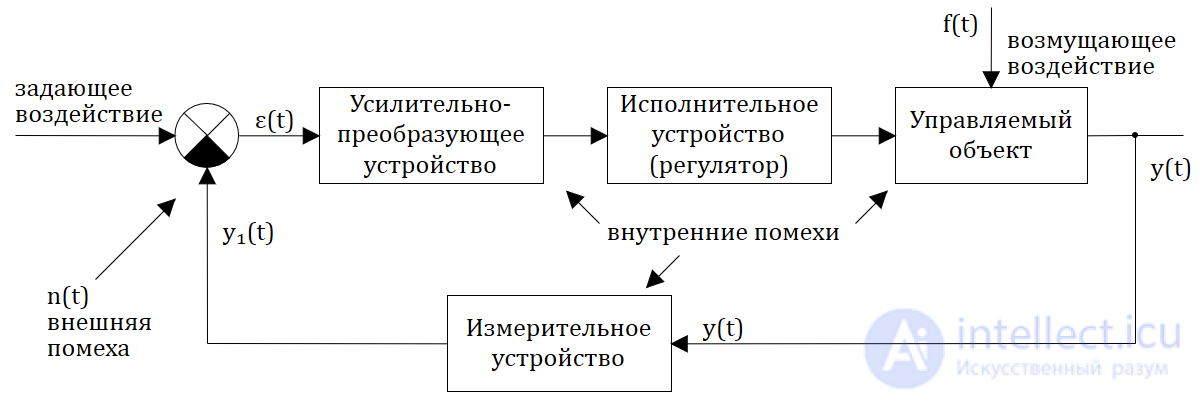
Рис. 1.2.3 — Структурная схема системы автоматического управления
Символом ε(t) или переменной ε(t) обозначается рассогласование (ошибка) на выходе сравнивающего устройства, которое может “работать” в режиме как простых сравнительных арифметических операций (чаще всего вычитание, реже сложение), так и более сложных сравнительных операций (процедур).
Так как y1(t) = y(t)*k1, где k1 — коэффициент усиления, то ==>
ε(t) = x(t) — y1(t) = x(t) — k1*y(t)
Задача системы управления состоит в том (если она устойчива), чтобы “работать” на уничтожение рассогласования (ошибки) ε(t), т.е. ==> ε(t) → 0.
Следует отметить, что на систему управления действуют как внешние воздействия (управляющее, возмущающее, помехи), так и внутренние помехи. Помеха отличается от воздействия стохастичностью (случайностью) своего существования, тогда как воздействие почти всегда детерминировано.
Для обозначения управляющего (задающего воздействие) будем использовать либо x(t), либо u(t).
Если вернуться к последнему рисунку (структурная схема САУ на рис. 1.2.3), то необходимо “расшифровать” роль, которую играет усилительно-преобразующее устройство (какие функции оно выполняет).
Если усилительно-преобразующее устройство (УПУ) выполняет только усиление (или ослабление) сигнала рассогласования ε(t), а именно: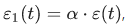 
, где α– коэффициент пропорциональности (в частном случае α = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление).
Если УПУ выполняет формирование выходного сигнала ε1(t), пропорционального ошибке ε(t) и интегралу от ε(t), т.е.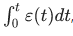 
, то такой режим управления называется пропорционально-интегрирующим (ПИ-управление). ==> 
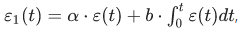, где b – коэффициент пропорциональности (в частном случае b = Const).
Обычно ПИ-управление используется для повышения точности управления (регулирования).
Если УПУ формирует выходной сигнал ε1(t), пропорциональный ошибке ε(t) и ее производной, то такой режим называется пропорционально-дифференцирующим (ПД-управление): ==> 
Обычно использование ПД-управления повышает быстродействие САУ
Если УПУ формирует выходной сигнал ε1(t), пропорциональный ошибке ε(t), ее производной, и интегралу от ошибки ==>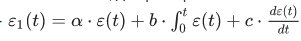
, то такой режим называетсято такой режим управления называется пропорционально-интегрально-дифференцирующим режимом управления (ПИД-управление).
ПИД-управление позволяет зачастую обеспечить “хорошую” точность управления при “хорошем” быстродействии.
Статистические характеризуются набором статистических параметров и функций распределения. Для их исследования используются методы математической статистики.
Адаптивные используют для описания объекта управления детерминированно-стохастические методы.
Гипотезы и аналоги, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам: такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Об этом говорит сайт https://intellect.icu . Другими словами, модель (лат. modulus – мера) – это объект – заместитель объекта – оригинала, обеспечивающий изучение некоторых свойств оригинала.
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.
Для математического моделирования линейных непрерывных САУ используются дифференциальные уравнения.
В непрерывных системах как входные воздействия, так и выходные процессы являются непрерывными функциями. Связь между ними отображается посредством дифференциальных уравнений, имеющих следующий вид:
|
|
(1) |
гдеx(t) иy(t) – задающее воздействие и выходной процесс, а переменные 
- их производные. Если функцииF1 иF2 – нелинейны относительно переменных, то системы будут нелинейными.
В линейных системахF1 иF2 – линейные функции. Если они явно зависят от времениt, то системы будут нестационарными. В случае стационарных систем явная зависимость функци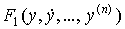й
и
от времени отсутствует. Величина старшей производнойn при выходной переменной в левой части уравнения называется порядком уравнения или порядком системы.
Если стационарная система допускает линеаризацию своих уравнений, то она описывается линейным дифференциальным уравнением следующего вида:
|
|
(2) |
где с иb – постоянные коэффициенты, зависящие от параметров системы. Все переменные входят в это уравнение линейно, что обеспечивает системе применимость принципа суперпозиции.
Так, если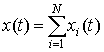
, то выходной процесс
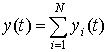, где каждой паре xi(t) и yi(t) соответствует уравнение (2).
Примером уравнения (2) является линеаризированное уравнение:
.
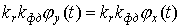Если обозначить
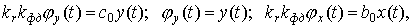
то мы получим частный случай уравнения (2).
Анализ линейной стационарной системы сводится к нахождению функцииy(t) по заданному воздействиюx(t). Иначе говоря, анализ САУ требует нахождения решения уравнения (2). Из соответствующих разделов высшей математики известно, что решение уравнения (2) состоит из двух слагаемых:
,
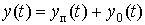гдеyп(t) переходная составляющая решения или переходный процесс системы, который находится из решения однородного уравнения
|
|
(3) |
при нулевых начальных условиях для самого процесса и его первых (n-1) производных.
Поясним смысл переходного процесса в САУ на примере следящей системы ФАП. Линеаризованное уравнение этой системы равно
|
|
(4) |
где x(t) = jx(t) – фаза входного воздействия генератора сигнала ГС, а y(t) = = jy(t) – фаза выходного сигнала подстраиваемого генератора ПГ.
Пусть задающее воздействие x(t) = 0, а в момент включения системы при t = 0 выходная фаза y(t) 
0.
Благодаря наличию начального рассогласования
система начинает работать, стремясь обеспечить значение фазы выходного
процесса y(t) = x(t) = 0. Это и будет переходный процессy П(t).
Так как по условию воздействиеx(t) = 0, то уравнение (4) для переходного процесса примет вид
,
что является однородным уравнением для (4).
Его решение легко находится и имеет вид
.
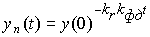Экспоненциальный характер переходного процесса показан на рис. 11.
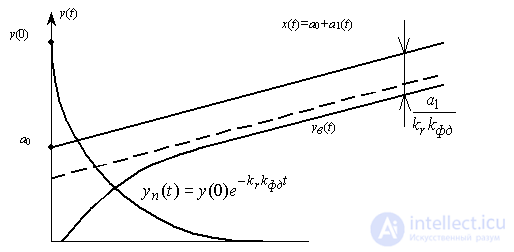
Рис. 11. Переходный и вынужденный процессы в системе ФАП
Теперь займемся вынужденным процессомyв(t). Он определяется только задающим воздействиемx(t) при нулевых начальных условиях в системе. Для нахожденияyв(t) надо определить частное решение неоднородного уравнения
|
|
(5) |
при нулевых начальных условиях и заданной функцииx(t).
Для рассмотрения системы ФАП уравнение вынужденного процесса примет вид
.
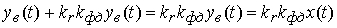Для примера положим
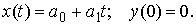
Воспользовавшись выражением общего решения дифференциального уравнения первого порядка, можно записать, что
.
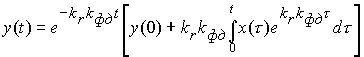Отсюда легко получить вынужденный процесс ФАП, полагая
y(t) = 0; x(t) = a0 + a1t:
.
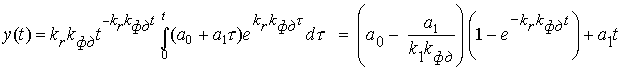Характер этой зависимости показан на рис. 11. С течением времени при t выходной процесс будет стремиться к функции
,
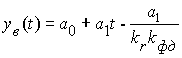то есть фаза выходного сигнала будет меньше фазы входного на величинуa1/krkфд и система слежения будет работать с некоторой ошибкой.
Важно подчеркнуть, что благодаря нулевым начальным условиям вынужденный процессyв(t) начинается с нуля.
На основании принципа суперпозиции итоговый процесс в системе
y(t) = yп(t) + yв(t).
Таким образом, исследование линейных стационарных систем автоматического управления сводится к отдельному исследованию характеристик переходных и вынужденных процессов, методы определения которых, как правило, оказываются различными.
Закон управления - это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t). Эта зависимость может быть представлена в виде
u(t) = F(x, g, f), (8.1)
где F - некоторый оператор от отклонения x, задающего воздействия g и возмущающего воздействия f, а также от их производных и интегралов по времени.
Обычно выражение (8.1) может быть записано следующим образом:
u(t) = F1(x) + F2(g) + F3(f). (8.2)
Здесь первое слагаемое соответствует управлению по отклонению, второе и третье - управлению по внешнему воздействию.
В зависимости от вида оператора F законы управления делятся на стандартные и специальные.
Стандартные законы управления - это универсальные законы, с помощью которых можно решать задачи автоматизации разнообразных технологических процессов и объектов.
Специальные законы управления - это законы, формируемые для решения конкретных задач.
Если для формирования управляющего воздействия u(t) используются только линейные математические операции, то такой закон управления называется линейным, в противном случае - нелинейным.
Линейный стандартный закон управления имеет следующий вид:
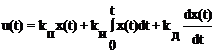, (8.3)
где первое слагаемое является пропорциональной, второе - интегральной, третье - дифференциальной составляющими закона, а коэффициенты kП, kИ и kД определяют вклад каждой из составляющих в формируемое управляющее воздействие.
Интегральная составляющая закона управления вводится для повышения точности, а дифференциальная - для повышения быстродействия работы системы.
Регулятор, формирующий управляющее воздействие в соответствии с (8.3), имеет передаточную функцию
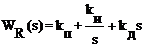. (8.4)
Структурная схема линейного стандартного регулятора приведена на рис.8.1.
Настройка такого регулятора заключается в задании значений коэффициентов kП, kИ, kД таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.
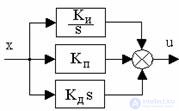
Рис. 8.1. Структура линейного стандартного регулятора
На практике широкое распространение получили типовые или промышленные регуляторы, представляющие собой универсальные автоматические устройства, легко приспосабливаемые для автоматизации разнообразных технологических процессов и объектов. При этом объект управления, как правило, является звеном статического типа, т.е. WОУ(0)=kОУ, где kОУ - коэффициент передачи объекта управления. Типовые регуляторы реализуют типовые законы управления, являющиеся частными случаями линейного стандартного закона управления, и классифицируются следующим образом.
П-регуляторы. Реализуют П-закон или пропорциональный закон управления
u(t) = kП x(t).
Передаточная функция П-регулятора
WR(s) = kП.
Пропорциональное управление позволяет уменьшить установившуюся ошибку в объекте в (1+k) раз, где k = kП´kОУ - коэффициент передачи разомкнутой системы. Регулирование в этом случае получается статическим, так как при любом конечном значении коэффициента передачи разомкнутой системы установившаяся ошибка будет отличной от нуля.
И-регуляторы. Реализуют И-закон или интегральный закон управления
u(t) = 
.
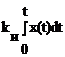Передаточная функция И-регулятора
.
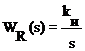При интегральном управлении получается система, астатическая по отношению к задающему воздействию. Повышение степени астатизма приводит к увеличению установившейся точности системы, но одновременно снижает ее быстродействие, а также приводит к ухудшению устойчивости. Снижение быстродействия объясняется тем, что в первый момент времени при появлении ошибки управляющее воздействие равняется нулю и только затем начинается его рост. В системе пропорционального управления рост управляющего воздействия в первые моменты времени происходит более интенсивно, так как наличие ошибки сразу дает появление управляющего воздействия, в то время как в системе интегрального управления должно пройти некоторое время.
ПИ-регуляторы. Реализуют ПИ-закон или пропорционально-интегральный закон управления
u(t) = kП x(t) +.
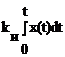Передаточная функция ПИ-регулятора
,
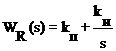
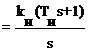где TИ = kП/ kИ.
Пропорционально-интегральное (изодромное) управление сочетает в себе высокую точность интегрального управления (астатизм) с большим быстродействием пропорционального управления. В первые моменты времени при появлении ошибки система с ПИ-регулятором работает как система пропорционального регулирования, а в дальнейшем начинает работать как система интегрального управления.
ПД-регуляторы. Реализуют ПД-закон или пропорционально-диф-ференциальный закон управления
.
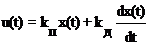Передаточная функция ПД-регулятора
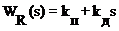= kП(TДs + 1),
где TД = kД/ kП.
Пропорционально-дифференциальное управление применяются для повышения быстродействия работы системы.
Регулирование по производной не имеет самостоятельного значения, так как в установившемся состоянии производная от ошибки равна нулю и управление прекращается. Однако она играет большую роль в переходных процессах, потому что позволяет учитывать тенденцию к росту или уменьшению ошибки. В результате увеличивается скорость реакции системы, повышается быстродействие, снижается ошибка в динамике.
ПИД-регуляторы. Реализуют ПИД-закон или пропорционально-интегрально-дифференциальный закон управления, соответствующий линейному стандартному закону вида (8.3).
ПИД-регулятор, представляющий собой астатический изодромный регулятор с предвидением, обеспечивает повышенную точность и повышенное быстродействие системы.
Прочтение данной статьи про законы управления позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое законы управления, закон управления, пид регуляторы, математические модели сау и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
;
; 
,
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления