Лекция
Привет, Вы узнаете о том , что такое идентификация матичестических моделей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое идентификация матичестических моделей , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Идентификация динамических объектов в общем случае состоит в определении их структуры и параметров по наблюдаемым данным – входному воздействию и выходным величинам.
В этом случае объект (элемент системы, объект управления, элемент технологического процесса и т. п.) представляет собой "черный ящик". Исследователю необходимо, подвергая объект внешним воздействиям и анализируя его реакции, получить математическую модель (описание его структуры и параметров), то есть превратить "черный ящик" в "белый ящик", добиться его "информационной прозрачности". Графически процесс идентификации иллюстрирует рис. 1.

Рис. 1
Важным моментом этого процесса является выбор точек приложения внешних воздействий и сбор информации о реакциях объекта, то есть размещение управляющих устройств и датчиковых систем.
Решается при идентификации объектов и более простая (относительно простая) задача, это задача идентификации параметров, когда заранее известна структура математической модели объекта, но не известны ее параметры. В этом случае говорят о переходе от "серого ящика" к "белому ящику". Графически процесс идентификации параметров иллюстрирует рис. 2.

Рис. 2
Задача идентификации параметров может либо входить компонентом в общую задачу идентификации объекта, либо решаться самостоятельно.
Рассмотрим на обобщенной структуре и процедуре процесса идентификации основы подхода к решению задач идентификации. Обобщенная структура процесса идентификации показана на рис. 3.
Обобщенная процедура идентификации
Классификация объекта.
Выбор для определенного класса объекта настраиваемую модель, то есть модель, структуру и параметры которой можно менять в процессе идентификации.
Выбрать критерий (оценку) качества идентификации, характеризующий в виде функционала доступных для наблюдения переменных отличие модели и объекта.
Выбрать алгоритм идентификации (механизм настройки модели), обеспечивающий сходимость процесса идентификации, минимум критерия качества идентификации.

Рис. 3
Методы идентификации принято разделять на две группы:
активная идентификация – идентификация вне контура управления,
пассивная идентификация – идентификация в контуре управления.
Активная идентификация
В этом случае объект исследования выводится из условий нормальной окружающей среды (нормальный режим эксплуатации, номинальные параметры рабочего режима и т. п.). Исследования проводятся в специализированных лабораторных условиях, как это показано на рис. 4. На входы объекта (рабочие и дополнительные) подаются тестовые сигналы специального вида. Это могут быть:
ступенчатые и импульсные временные сигналы,
гармонические сигналы,
случайные воздействия с заданными параметрами.
Активную идентификацию используют при разработке новых технологий применительно к действующим промышленным объектам, в изучении новых явлений, в первоначальной разработке математической модели.
Пассивная идентификация
При пассивной идентификации объект функционирует в контуре управления, находится в процессе нормальной эксплуатации. На его входы поступают только естественные сигналы управления.
Пассивную идентификацию используют для уточнения математической модели, для слежения за изменениями в объекте. Информация оперативно используется в системе управления объектом, процесс такой идентификации иллюстрируется рис. 5.
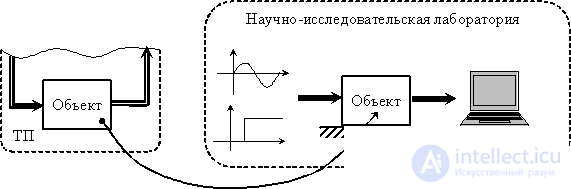
Рис. 4

Рис. 5
Кроме перечисленных групп методов реализуются и системы идентификации смешанного типа, когда объект не выводится из нормального режима эксплуатации, но к управляющим сигналам добавляются тестовые воздействия, позволяющие идентифицировать объект, не ухудшая качества основного процесса управления.
Более подробно рассмотрим активную идентификацию.
Активная идентификация объектов управления может производиться как во временной области, так и в частотной области. Об этом говорит сайт https://intellect.icu . При этом В каждой области используют собственные алгоритмы и методы идентификации.
При активной идентификации в большинстве случаев используют полученные в результате экспериментов характеристики:
частотные характеристики (АФЧХ, ЛАЧХ, ЛФЧХ и др.),
временные характеристики (ступенчатое изменение задания, "узкий" импульс задания и др.).
Рассмотрим в качестве примера один из подходов решения задачи идентификации структуры и параметров объекта в частотной области. Ограничим рассмотрение объектом с одним входом и одним выходом.
Мы знаем, что если имеется математическая модель такого объекта в виде передаточной функции –
|
|
(1) |
то это соответствует наличию полной информации о структуре и параметрах объекта, всех его характеристиках.
Преобразуем передаточную функцию (1) к полюсно-нулевому представлению, форме Боде –
|
|
(2) |
где 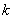 – коэффициент усиления (
– коэффициент усиления (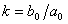 ),
), 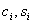 – соответственно полюсы и нули передаточной функции.
– соответственно полюсы и нули передаточной функции.
Если среди корней ( ) встречаются комплексно сопряженные пары корней, то разложение (2) необходимо дополнить сомножителями следующего типа –
) встречаются комплексно сопряженные пары корней, то разложение (2) необходимо дополнить сомножителями следующего типа –
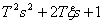 .
.
Предполагая для простоты изложения отсутствие комплексно сопряженных корней, можно преобразовать (2) к следующему виду –
|
|
(3) |
где
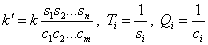 .
.
По выражению для передаточной функции в виде (3) получим частотную характеристику объекта –
 ,
,
ЛАЧХ –
|
|
(4) |
ЛФЧХ –
|
|
(5) |
С другой стороны, нам известно, что ЛАЧХ и ЛФЧХ динамических звеньев с передаточными функциями –
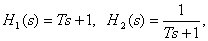
имеет вид, показанный на рис. 6, так как звенья являются соответственно форсирующим и апериодическим динамическими звеньями первого порядка.

Рис. 6
Исходя из изложенного материала, можно предложить следующую процедуру активной идентификации структуры и параметров линейной системы с одним входом и одним выходом:
В процессе эксперимента с объекта снимается частотная характеристика в виде ЛАЧХ и ЛФЧХ.
Полученная экспериментально ЛАЧХ аппроксимируется кусочно-линейной криво1 – набором отрезков (асимптот) с целочисленным наклоном кратным 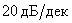 .
.
По наклону асимптот и частотам сопряжения асимптот определяется передаточная функция объекта в виде произведения передаточных функций соответствующих асимптотам элементарных динамических звеньев (апериодических и форсирующих).
При наличии в полученной ЛАЧХ и ЛФЧХ признаков звеньев второго порядка, то есть асимптот с наклоном кратным 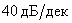 , необходимо ввести такие звенья в модель.
, необходимо ввести такие звенья в модель.
Колебательное звено с передаточной функцией –
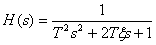 ,
,
имеет ЛАЧХ и ЛФЧХ, показанные на рис. 7.

Рис. 7
Форсирующее звено второго порядка с передаточной функцией
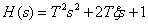 ,
,
имеет ЛАЧХ (ЛФЧХ) симметричные показанным на рис. 7 характеристикам колебательного звена относительно оси частот.
Рассмотрим пример идентификации по рассмотренной процедуре.
Пример
По экспериментально полученной ЛАЧХ объекта определить передаточную функцию.
Решение
Аппроксимируем экспериментальную ЛАЧХ набором асимптот, как это показано на рис. 8.
Рассмотрим теперь участки аппроксимированной ЛАЧХ, на которых наклон не изменяется:
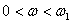 .
.
На этом интервале виду асимптоты соответствует ЛАЧХ интегрирующего звена, его передаточная функция –
 .
.
Этому звену соответствует следующее выражение ЛАЧХ –
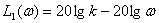 .
.
Используем последнее выражение для определение 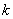 , подставив значение характеристики при частоте
, подставив значение характеристики при частоте 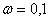
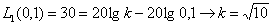 .
.

Рис. 8
 .
.
На этом интервале наклон асимптоты возрос на 20 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией –
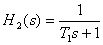 ,
,
где постоянная времени определяется по точке сопряжения асимптот –
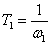 .
.
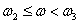 .
.
На этом интервале наклон асимптоты уменьшился на 20 дБ/дек, что соответствует добавлению форсирующего звена первого порядка с передаточной функцией –
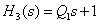 ,
,
где постоянная времени определяется по точке сопряжения асимптот –
 .
.
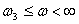 .
.
На этом интервале наклон асимптоты возрос на 20 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией –
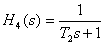 ,
,
где постоянная времени определяется по точке сопряжения асимптот –
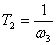 .
.
Перемножая полученные передаточные функции, получим передаточную функцию объекта –
 .
.
Контрольные вопросы и задачи
Дайте определение процессу идентификации объекта, идентификации параметров.
Какие методы относят к методам пассивной идентификации?
Какие методы относят к методам активной идентификации?
Поясните процедуру идентификации параметров объекта управления по его экспериментальной ЛАЧХ.
Асимптотическая ЛАЧХ объекта имеет вид –

Определите передаточную функцию объекта.
Ответ:
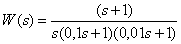 .
.
Асимптотическая ЛАЧХ объекта имеет вид –

Определите передаточную функцию объекта.
Ответ:
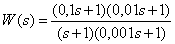 .
.
Асимптотическая и точная ЛАЧХ динамического звена имеет вид –

Определите передаточную функцию звена.
Ответ:
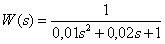 .
.
Прочтение данной статьи про идентификация матичестических моделей позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое идентификация матичестических моделей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про идентификация матичестических моделейОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления