3.2 Модели управляемых систем

Привет, Вы узнаете о том , что такое модели управляемых систем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое модели управляемых систем , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

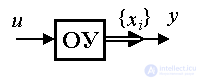
3.2.1. Модели вход-состояние-выход. Сначала рассмотрим частный случай управляемой динамической системы с одним входом u(t) и одним выходом y(t) , описываемой уравнением [M1a] , где a₀=1. Введем в рассмотрение переменные состояния (3.1). Дифференцируя (3.3) по времени и подставив [M1a] , находим уравнения состояния:

(3.38)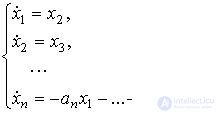                     

При этом уравнение выхода по-прежнему имеет вид (3.8). Уравнения (3.38) и (3.8) представляют собой простейший случай модели вход-состояние-выход (ВСВ).

В более общем случае модель ВСВ управляемой динамической системы [ М1 ] содержит уравнения состояния вида:

[М4]                     

и уравнение выхода [М5]. Для их преобразования к компактной векторно-матричной форме необходимо определить вектор состояния 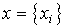 ,  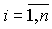, матрицы  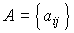,  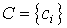, а также матрицу входа размера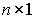 

                      .

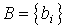
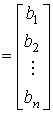Тогда уравнения [М4], [М5], описывающие модель вход-состояние-выход, принимают вид:

[М6]                      ,

[М7]                      ,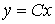

где  .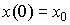

Модель [М6] и [М7] связывает вход  и выход 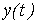 через промежуточные переменные  .

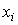В частном случае, когда модель ВСВ представлена в форме ( 3.38), (3.8 ), получаем матрицы

                     , ,  .

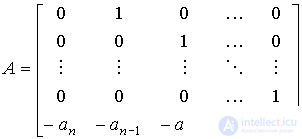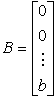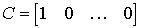Аналогично получается модель ВСВ многоканальной (многосвязной) системы (см. модель [M2m]). В общем случае она содержит уравнения состояния вида

[М4m]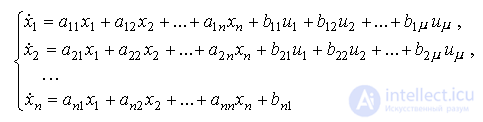           

и уравнения выходов [М5m] . Определим 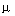 -мерный вектор управления: 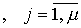  и m -мерный вектор выходов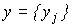 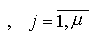  , а также матрицы

                     , 

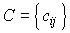
размерност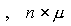и  и 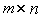 , соответственно. Тогда уравнения [M4m] и [M5m] можно переписать в виде [M6] и [M7].

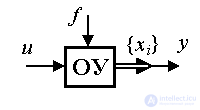
Рассмотрим возмущенную динамическую систему, (см. [М1f]), т.е. управляемую систему на вход которой дополнительно действует входной сигнал ( возмущающее воздействие ) 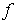 (t ). Уравнение состояния такой системы записывается в виде:

[М4f]                      ,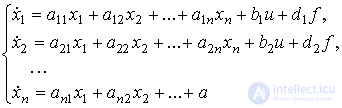

где d_i , 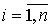 , - коэффициенты, а уравнение выхода сохраняет форму [M5]. Векторно-матричная форма модели [M4f] имеет вид :

[М6f]                      ,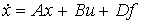

[M7]                     y=Cx,

где   .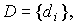

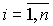Если на вход системы действует несколько возмущающих воздействий f_k , то в уравнении [M6f] 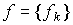 - вектор возмущений, и  .

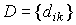В частном случае (см. Об этом говорит сайт https://intellect.icu . (3.35) ) уравнения состояния возмущенной системы принимают вид

(3.39)                     

и в уравнении [М6f]

                     .

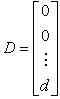Рассмотрим решения уравнений [М6], [М7], полагая 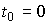 . Решение уравнения состояния [M6] можно представить в виде:

(3.40)                      ,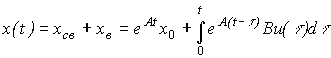

где 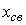 (t) - свободная составляющая (переходный процесс автономной системы), соответствующая решениям однородного дифференциального уравнения [M6a] и зависящая от начальных условий  ,  (t) - вынужденная составляющая, соответствующая переходному процессу системы [M6] при нулевых начальных условиях 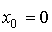 (реакция системы на входное воздействие u(t)).

Подставляя (3.40) в уравнение выхода [M7] , получаем

(3.41)                      ,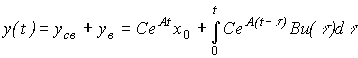

где

(3.42)                      .

Отметим, что матрица

(3.43)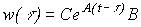                     

является весовой (импульсной переходной) матрицей (при 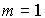 - весовой функцией) и , следовательно , уравнение (3.42) совпадает с приведенным ранее выражением (2.35).

Для возмущенных моделей ВСВ решения могут быть получены в аналогичной форме.

3.2.2. Передаточная функция (матрица) модели ВСВ и структурные схемы. Приведенные выше уравнения, описывающие модели вход-состояние-выход , могут быть записаны в операторной форме (см. 2.1). Рассмотрим уравнения [M6a], [M7]. Используя оператор дифференцирования p=d/dt, запишем 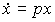. Тогда из уравнение состояния [M6a] после простейших алгебраических преобразований находим

(3.44)                      .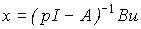

Подставляя последнее выражение в уравнение выхода [M7] получаем

(3.45)                      .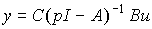

Введем обозначение

(3.46)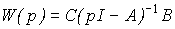                     

и запишем предыдущее уравнение в виде

(3.47)                      .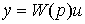

Сравнение с уравнением [M3m] показывает, что матричный интегро-дифференциальный оператор W(p) есть не что иное, как передаточная матрица управляемой динамической системы (см. п. 2.1.3 ).

Рассмотрим свойства оператора (3.4 6). Матрица 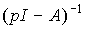 называется резольвентой и может быть представлена в виде

(3.48)                      ,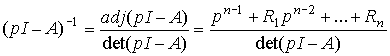

где 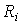 - числовые матрицы  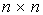. Тогда

(3.49)                      ,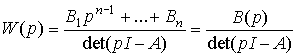

где  ;  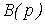- матричный оператор.

Для случая одноканальной системы ( m= 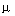 =1) W(p) - передаточная функция. Принимая во внимание уравнение (3.48), найдем, что

(3.50)                      -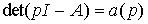

характеристический полином системы; а

(3.51)                      -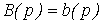

характеристический полином правой части дифференциального уравнения (см. п. 2.1.1). Следовательно, собственные числа матрицы A в точности совпадают с корнями характеристического уравнения (полюсами) системы

(3.52)                      .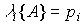

Для построения структурной схемы, соотвествующей модели ВСВ, перепишем уравнение состояния [М6] в операторном виде

(3.53)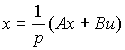                     

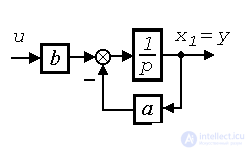
и воспользуемся также уравнением выхода [М7 ]  . Структурная схема системы принимает вид, представленный на рис. 3.2 .

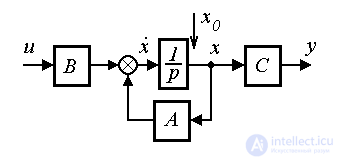
Рис. 3. 2. Структурная схема модели ВСВ

В частном случае, когда уравнения состояния записаны в форме (3.38), (3.8) найдем

(3.54)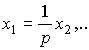                     

(3.55)                      .

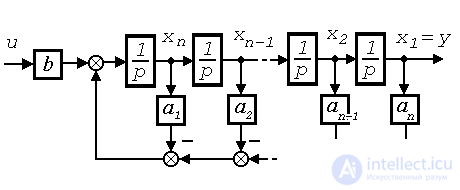
Рис. 3.3. Структурная схема модели ( 3.38), (3.8)

Структурная схема приведена на рис. 3.3 и соотвествует кононической управляемой форме представления линейной системы (см. п. 3.3.2)

3.2.3. Статический режим. Рассмотрим поведение модели ВСВ при постоянном входном (управляющем) воздействии, т.е.  . В этом случае решение дифференциального уравнения [М6а] соответствует установившейся составляющей переходного процесса и ищется в виде 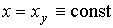 .Замечая, что 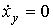находим:

(3.56)                      .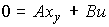

При условии, что 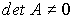 , ( т.е.  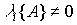) , алгебраическое уравнение (3.56) единственным образом разрешимо относительно x _у :

(3.57)                      .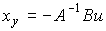

Подставляя найденное решение в уравнение выхода [М7], находим статическую характеристику системы [М6а], [М7]

(3.58)                      .

Принимая во внимание выражение (2.47), с очевидностью можно записать

(3.59)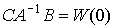                     

и получить выражение (2.46).

Если система такова, что  , то матрица A необратима и система не имеет статического режима (см. п. 2.2.5).

Пример 3.1. Рассмотрим систему второго порядка ( n =2), модель ВВ которой представлена уравнением

(3.60)                      .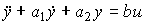

Переменные состояния определяются выражениями

(3.61)                      ;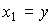 

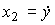
и модель ВСВ находятся как

(3.62)                       ,

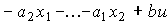(3.63)                      .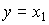

Векторно-матричная форма модели имеет вид

(3.62а)                       ,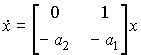

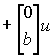(3.63а)                      .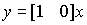

Пример 3.2. 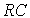 - цепь, рассмотренная в п. 1.1.2, описывается дифференциальным уравнением первого порядка:

(3.64)                      .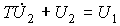

Введем обозначения

(3.65)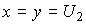                     

и

(3.66)                      .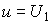

Уравнение (3.64) принимает вид

(3.67)                      ,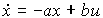

(3.68)                      ,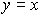

где 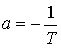 и  .

Пример 3.3. Рассмотрим дифференциальное уравнение второго порядка

                     ,

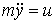описывающее движение материальной точки (см. пример 2.3).

Уравнение приводится к виду

(3.69)                      ,

где  . Введем в рассмотрение переменные состояния

(3.70)                      ,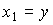

(3.71)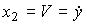                     

и найдем модель ВСВ как

(3.72)                       ,

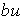(3.73)                      .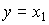

Векторно-матричная форма модели имеет вид

                     ,

                     .

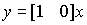Это частный случай ранее рассмотренной модели (3.62а ), ( 3.63а ).

Прочтение данной статьи про модели управляемых систем позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое модели управляемых систем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про модели управляемых систем