19 Квадратичная интегральная оценка с учетом производной

Привет, Вы узнаете о том , что такое квадратичная интегральная оценка с учетом производной, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое квадратичная интегральная оценка с учетом производной , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Недостатком квадратичной интегральной оценки , как и предыдущих оценок, является то, что при минимизации оценки не накладываются ограничения на форму переходного процесса. На пример, показанные на рис. 1 графики  – (а, б, в) могут иметь одинаковые значения 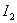 существенно при этом отличаясь по форме переходного процесса.

Рис. 1

Кроме того, часто оказывается, что выбранные по 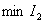 параметры системы приводят к существенно колебательному процессу, большим производным из-за стремления приблизить процесс к идеальному скачку.

Поэтому используют еще один вид интегрально квадратичной оценки, в которой ограничение накладывается не только на величину отклонения 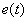, но и на скорость его изменения . Эта оценка имеет следующий вид –

(1)

где 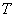 – некоторая постоянная времени.

Разницу между оценкам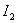и  и 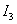 можно представить графически, как это показано на рис. 2.

Рис. 2

То есть оптимизированный по 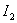 переходный процесс стремиться к идеальному скачку, а оптимизированный по  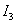– к кривой экспоненциального вида, которая описывается следующим выражением –

.

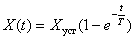Докажем последнее утверждение. Для этого проанализируем выражение (1).

,

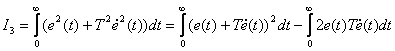с учетом того, что

,

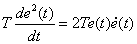получаем

(2)

С учетом того, что последнее слагаемое в (2) является величиной постоянной –

,

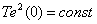квадратичная оценка 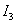 будет иметь минимум при

(3)

Решение дифференциального уравнения (3) имеет вид –

,

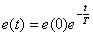а если перейти от ошибок к выходным переменным, то получим –

,

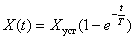что и требовалось доказать.

Следовательно, выбирая параметры системы по 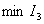, можно приблизить переходный процесс к экспоненте с заданной постоянной времени 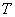, тем самым вводится ограничение на скорость нарастания выходной величины .

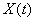Методика определения 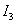 может быть аналогичной методике определения 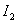, рассмотренной выше, если представить квадратичную оценку с учетом производной в следующем виде –

,

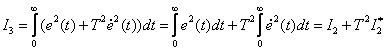где 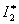 определяется по формулам для 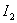, но с учетом того, что порядок числителя 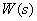–  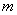увеличивается на 1.

В теории автоматического управления используют квадратичные оценки с производными более высокого порядка (до 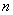) для более точного задания желаемой формы переходного процесса, естественно, что при этом усложняется и процесс вычисления оценок.

 

Вычисление квадратичных интегральных оценок

 

Рассмотрим вычисление и использование квадратичных ошибок на примере.

Пример

В системе управления с передаточной функцией –

,

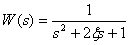зададим :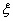

• из условия ,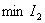

• из условия ,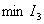

и сравним переходные процессы для двух этих случаев.

Решение

Получим выражение для . Об этом говорит сайт https://intellect.icu . Для этого преобразуем передаточную функцию системы к заданному виду

,

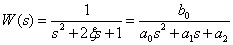тогда получим

(4)

Выражение для 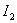 принимает вид –

(5)

Определим компоненты (5) по параметра передаточной функции системы (4).

(6)

Для нахождения 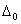 определим (), при ,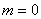 

,

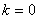
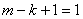Заменим в выражении (6) для  первый столбец столбцом вида

.

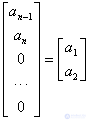Тогда получаем

.

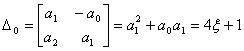Определим  –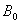

.

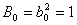После подстановки полученных компонент в (5) получаем выражение для квадратичной интегральной оценки.

(5)

Найдем выражение для частной производной по 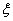 от выражения (5)

,

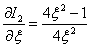приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .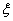

.

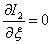В результате получаем оптимизированное по квадратичной оценке значение  –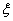

(6)

Передаточная функция системы при 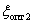 примет вид –

.

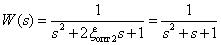На рис. 3 покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по 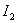 параметром.

Рис. 3

Таким образом, имеем следующие показатели качества переходного процесса,

(7)

Определим 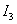 по отработанной выше методике для  –

,

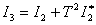выражение для 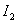 берем из предыдущего случая –

.

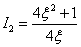Определим теперь 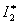. Передаточная функция системы для этого случая имеет вид –

,

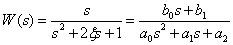тогда получим

(8)

Выражение для 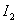 принимает вид –

(9)

Определим компоненты (9) по параметра передаточной функции системы (8).

(10)

Определим коэффициенты  –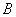

.

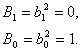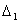не определяем, так как 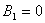. Для нахождения  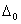определим (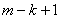), при , 

,

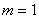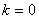
Заменим в выражении (10) для  второй столбец столбцом вида

.

Тогда получаем

.

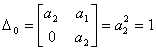После подстановки полученных компонент в (9) получаем выражение для квадратичной интегральной оценки.

(11)

Окончательно получаем

(12)

Найдем выражение для частной производной по 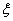 от выражения (12)

,

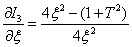приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .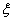

.

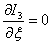В результате получаем оптимизированное по квадратичной оценке с учетом производной значение  –

(13)

Полагаем для определенности 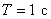, тогда

.

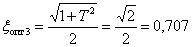Передаточная функция системы при 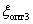 примет вид –

.

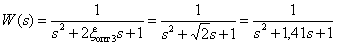На рис. 3 покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по 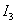 параметром.

Рис. 4

Таким образом, имеем следующие показатели качества переходного процесса,

(14)

Сравнивая переходные процессы, видим, что при оптимизации по квадратичной оценке с учетом производной (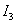) получили существенно меньшие значения перерегулирования и быстродействия, при более плавном нарастании переменной.

Контрольные вопросы и задачи

1. Дайте определение квадратичной интегральной оценки с учетом производной, поясните ее компоненты.

2. К какому виду стремиться переходный процесс при минимизации интегральной квадратичной оценки с учетом производной?

3. Как вычисляют квадратичную интегральную оценку с учетом производной?

4. Вычислите интегральную квадратичную оценку переходного процесса в системе с передаточной функцией –

,

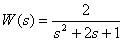если на вход системе подается единичная ступенчатая функция.

Ответ:

Интегральная квадратичная оценка .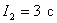

1. Вычислите интегральную квадратичную с учетом производной оценку переходного процесса в системе с передаточной функцией –

,

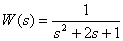если на вход системе подается единичная ступенчатая функция, а постоянная времени оценки .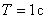

Ответ:

Интегральная квадратичная оценка .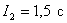

1. Определите параметр регулятора системы управления, обеспечивающий минимум квадратичной оценки

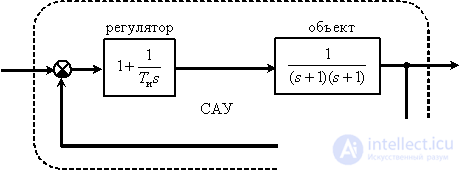
Ответ:

Параметр пропорционально-интегрального регулятора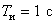 

Прочтение данной статьи про квадратичная интегральная оценка с учетом производной позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое квадратичная интегральная оценка с учетом производной и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про квадратичная интегральная оценка с учетом производной

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.