Лекция
устойчивость – свойство системы возвращаться в исходное состояние после какого-либо воздействия. Устойчивость — способность системы сохранять текущее состояние при влиянии внешних воздействий, может означать:
Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения. Устойчивая САУ — система, в которой переходные процессы являются затухающими.
— операторная форма записи линеаризированного уравнения.
y(t) = yуст(t)+yп = yвын(t)+yсв
yуст(yвын) — частное решение линеаризированного уравнения.
yп(yсв) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть 
САУ устойчива, если переходные процессы уn(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть 
при 
Решая дифференциальное уравнение в общем случае, получим комплексные корни pi, pi+1 = ±αi ± jβi
Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:
, где 
, 
Из полученных результатов видно, что:
, что приводит к расходящимся колебаниям;
, что приводит к незатухающим синусоидальным колебаниям системы (система на границе устойчивости) (теорема Ляпунова 3).Линейная динамическая система называется устойчивой, если после снятия возмущений при
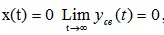, то есть движение затухает (рис. 6.1. а).
Система называется неустойчивой, если после снятия возмущений свободное движение стремится к ?, то есть при t??,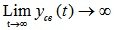
(рис. 6.1. б).
Система называется нейтральной, если после снятия возмущений x(t) свободное движение стремится к какому-то пределу M, то есть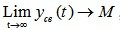 
, где 0<M (рис. 6.1. в).
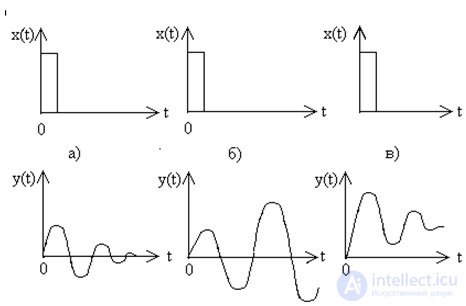
Рис.6.1. Свободное движение системы управления
В общем случае дифференциальное уравнение звена или системы имеет вид:
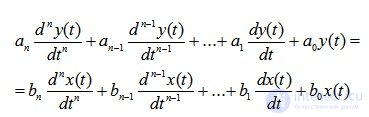(6.1)
Его общее решение
(6.2)
Составляющую решения в виде общего решения однородного уравнения называют свободным движением yсв(t) а составляющую в виде частного решения неоднородного уравнения называют вынужденным движением yвын(t), где yсв(t) определяется левой частью уравнения (6.1):
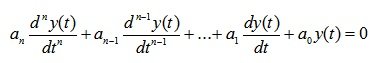(6.3)
Его характеристическое уравнение
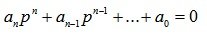(6.4)
Так как в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса (независимо от быстроты затухания переходного процесса), то устойчивость линейной системы не зависит от правой части дифференциального уравнения (6.1.) и полностью определяется его левой частью, то есть (6.3).
Уравнение движения системы представлено уравнением (6.1). Для анализа устойчивости исследуем уравнение (6.3). Его решение:
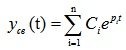
, где pi – корни характеристического уравнения (6.4).
Так как при ограниченном по абсолютной величине входном воздействии составляющая вынужденного движения также ограничена, то устойчивость системы обеспечивается при выполнении условия:
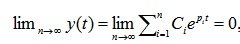(6.5)
который означает, что переходной процесс в системе затухает.
Рассмотрим случаи для корней различного вида.
Вещественные корни:
Если все pi =?, где ?i - действительно положительное число, то
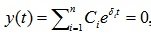
?i может иметь значения >0, <0, =0.
Из свойств экспоненциальной функции можем сделать вывод, что при ?i <0 и при t??, компонента y(t) является затухающей, то есть система устойчива.
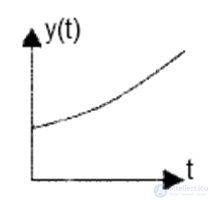
Рис. 6.2. ? > 0 (система неустойчива)
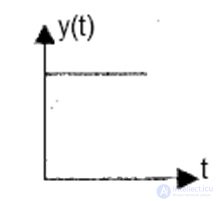
Рис. 6.3. ? = 0 (система на грани устойчивости)
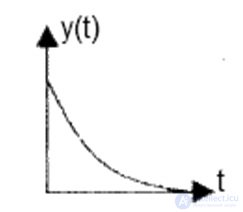
Рис. 6.4. ? < 0 (система устойчива)
Комплексно-сопряженные корни:
То есть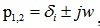 
, в этом случае компонента решения имеет вид:
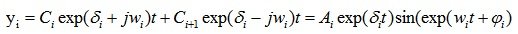(6.6)
где Ai, ?i, –константы, определяемые Ci, Ci+1, .
Графики зависимости yi от значения ?i приведены на рис.6.5 и 6.6
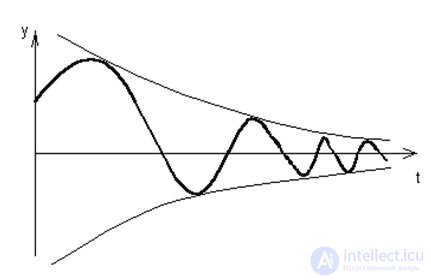
Рис. 6.5. Свободное движение системы для случая комплексных корней с отрицательной действительной частью
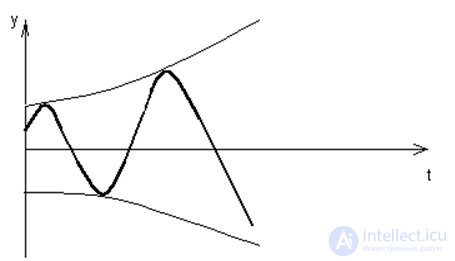
Рис. 6.6. Свободное движение системы для случая комплексных корней с положительной действительной частью .
В случае ?i=0, корни являются чисто мнимыми и график функции представляет собой незатухающие гармонические колебания.
Из проведенного анализа следует, что линейная динамическая система будет устойчива тогда и только тогда, когда действительная часть корней характеристического уравнения будет отрицательной. Это есть необходимое и достаточное условие устойчивости линейной системы управления.
Следует отметить, что ни одна реальная система управления не является строго линейной. Линейные характеристики звеньев и линейные дифференциальные уравнения получаются путем линеаризации реальных характеристик и уравнений.
Ляпуновым доказано, что если линеаризованная система устойчива, то реальная система при малых отклонениях также устойчива; если линеаризованная система неустойчива, то реальная система тоже неустойчива; если линеаризованная система нейтральная или находится на колебательной границе устойчивости, то судить об устойчивости реальной системы затруднительно, так как малые нелинейные члены могут коренным образом изменить вид переходного процесса, сделав систему устойчивой или неустойчивой.
Недостатком прямого метода исследования устойчивости системы является необходимость вычисления корней характеристического уравнения, что связано с определенными трудностями.
Существуют критерии устойчивости, которые позволяют, не решая уравнения, ответить на вопрос: устойчива или неустойчива система управления.
Для определения устойчивости системы строятся таблицы вида:
| Коэффициенты | Строки | столбец 1 | столбец 2 | столбец 3 |
|---|---|---|---|---|
| 1 |  |
 |
 |
|
| 2 |  |
 |
 |
|
 |
3 |  |
 |
 |
 |
4 |  |
 |
 |
Для устойчивости системы необходимо, чтобы все элементы первого столбца имели положительные значения; если в первом столбце присутствуют отрицательные элементы — система неустойчива; если хотя бы один элемент равен нулю, а остальные положительны, то система на границе устойчивости.
— определитель Гурвица
Теорема: для устойчивости замкнутой САУ необходимо и достаточно, чтобы определитель Гурвица и все его миноры были положительны при 
Одним из наиболее распространенных алгебраических критериев устойчивости является критерий устойчивости Рауса-Гурвица, который был разработан в конце 19 века. Он основан на анализе коэффициентов характеристического полинома и сводится к проверке удовлетворения n неравенств (n порядок характеристического полинома). Порядок проверки устойчивости АС по данному критерию следующий. Из коэффициентов характеристического полинома
полагая, что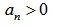 
составляется главный определитель Гурвица.
Система устойчива, если определитель Гурвица и все определители низшего порядка больше 0
Определитель Гурвица
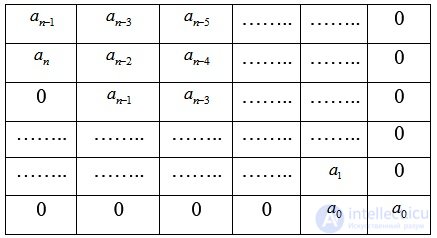(6.7)
Из главного определителя Гурвица выделяются определители Гурвица низшего порядка (миноры).
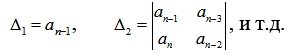(6.8)
Номер определителя Гурвица соответствует его размерности.
Критерий Рауса-Гурвица формулируется следующим образом: для того, чтобы линейная система автоматического управления была устойчива, необходимо и достаточно, чтобы при все определители Гурвица были положительными, т.е.
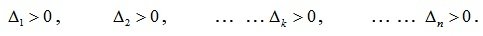
Чтобы линейная система уравнений была устойчива, необходимо и достаточно положительности диагональных миноров матрицы Гурвица при условии a0>0. Можно показать, что для уравнений первого и второго порядков условием устойчивости, по Гурвицу, является положительность их коэффициентов.
Как и при использовании критерия Гурвица исходной информацией для использования критерия Михайлова является характеристическое уравнение исследуемой системы. Здесь применяется геометрическая иллюстрация траектории движения конца вектора Михайлова – годограф Михайлова.
На основе характеристического уравнения замкнутой системы (6.4) вводится в рассмотрение некоторая функция комплексного переменного, полученная заменой p=j?:
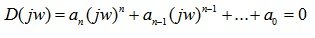(6.9)
Функцию (6.9) можно представить в виде
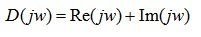(6.10)
На комплексной плоскости Re-Im вектор D(j?) опишет при изменении ? от 0 до ? кривую – годограф Михайлова.
Для устойчивой системы управления n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении ? от 0 до ?, начиная с вещественной положительной полуоси, проходил против часовой стрелки последовательно через n– квадрантов.
На рисунке 6.7 приведен годограф Михайлова для различных случаев.
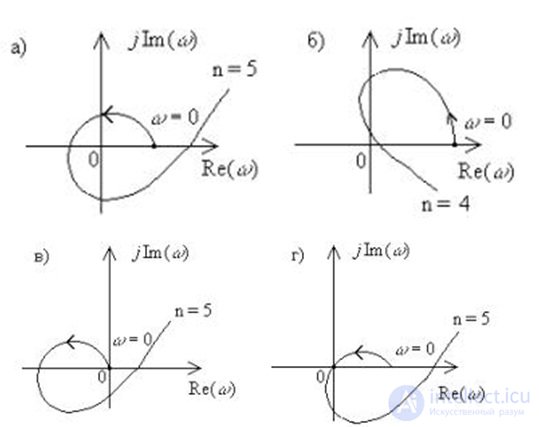
Рис. 6.7. Примеры для случаев: а) устойчивой, б) неустойчивой систем, в) случай нейтральной системы с нулевым корнем, г) случай колебательной границы устойчивости.
Обратимся к рис.6.8, иллюстрирующему устойчивую системы автоматического регулирования. Для устойчивой системы автоматического регулирования наблюдается чередование корней действительной Re(?) и мнимой jIm(?) частей (следствие из критерия Михайлова).
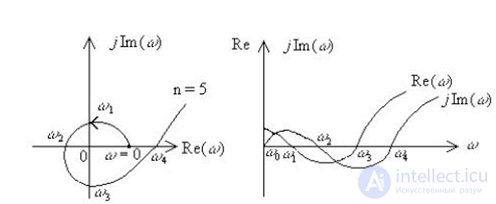
Рис. 6.8. Изменение вещественной и мнимой составляющих вектора Михайлова при изменении частоты
Недостатком алгебраических критериев и частотного критерия устойчивости является их ограниченность системами без транспортного запаздывания. В случае системы с транспортным запаздыванием их применение дает приближенную оценку устойчивости в пределах правомерности аппроксимации звена транспортного запаздывания рядом Паде.
В 1932 году американский ученый Г.Найквист показал, что существует определенная связь между устойчивостью и видом АФЧХ усилителей с отрицательной обратной связью, а в 1936 году советский ученый А.В. Михайлов распространил предложенный критерий на системы автоматического управления. Частотный критерий устойчивости Найквиста –Михайлова, который позволяет судить об устойчивости замкнутой системы автоматического регулирования по ее амплитудно – частотной характеристике в разомкнутом состоянии. Поскольку последняя может быть получена экспериментально, то этот критерий нашел широкое распространение.
АС, неустойчивая в разомкнутом состоянии, может оказаться устойчивой в замкнутом состоянии. Это становится очевидным после анализа критерия Найквиста-Михайлова.
Этот критерий позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой системы.
Для минимально-фазовых систем этот критерий формулируется следующим образом: для того, что бы автоматическая система, устойчивая или нейтральная в разомкнутом состоянии, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы не охватывал точку М{-1, j0} на комплексной плоскости при изменении частоты ? от нуля до бесконечности и повороте вектора АФЧХ W(j?) по часовой стрелке .
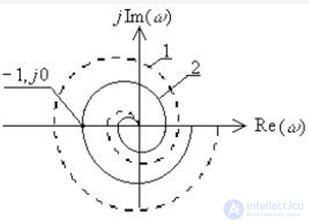
Рис. 6.9. Пример неустойчивой замкнутой системы при устойчивой разомкнутой системе (1) и положения системы на границе устойчивости (2)
запас устойчивости по модулю и по фазе
На рис.6.10. показана амплитудно-фазовая характеристика разомкнутой системы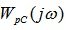 
и окружность с радиусом R=1.
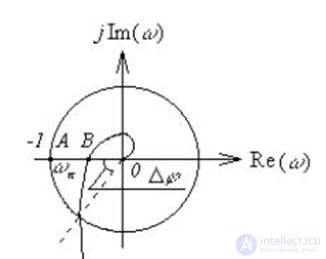
Рис. 6.10. К определению запаса устойчивости по модулю и по фазе
Запас устойчивости по модулю определяется величиной отрезка АВ. Он показывает, на какую величину нужно увеличить амплитуду амплитудно-фазовой характеристики разомкнутой системы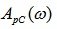 
без изменения фазы, чтобы замкнутая система вышла на границу устойчивости:
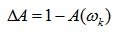(6.11)
Запас устойчивости по фазе определяется величиной
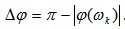(6.12)
Он показывает, на какую величину по часовой стрелке нужно повернуть по фазе без изменения амплитуды вектор амплитудно-фазовой характеристики разомкнутой системы, чтобы замкнутая система вышла на границу устойчивости.
Устойчивость замкнутой САР с использованием логарифмического критерия можно определить, построив совмещенные ЛАЧХ и ЛФЧХ разомкнутой системы.
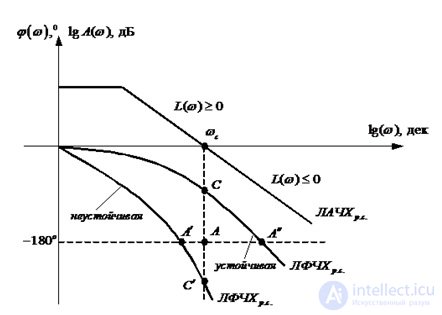
Рис. 6.11. Устойчивость системы по ЛАЧХ и ЛФЧХ
Замкнутая система автоматического управления устойчива, если при L(w)?0 соответствующая ЛФЧХ проходит таким образом, что фаза ?(w) не превосходит значения -180°(-?).
Система устойчивая в разомкнутом состоянии будет устойчивой и в замкнутом, если точка А ЛФЧХ определяемая фазой -180°(-?) соответствует области отрицательных значений логарифмической амплитуды L(w) ;
Важным показателем работоспособности АС служат запасы устойчивости по амплитуде и по фазе.
Запас устойчивости по фазе определяется как возможная величина приращения ЛФХ до достижения границы устойчивости: ??3 = ? + ? (Wср).
Запас устойчивости по амплитуде определяется как возможная величина приращения ЛАЧХ ( т.е. коэффициента усиления), при котором АС сохраняет устойчивость L3=20lgR(w?)|.
В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать систему так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.
Необходимость запаса устойчивости определяется следующими условиями:
Частотный критерий Найквиста применим, главным образом, когда трудно получить фазовые характеристики экспериментально. Однако вычисление АФХ, особенно частотных, сложнее, чем построение кривых Михайлова. Кроме того, расположение АФЧХ не дает прямого ответа на вопрос: устойчива ли система, то есть требуется дополнительное исследование на устойчивость системы в разомкнутом состоянии.
Критерий Михайлова применяется для систем любого порядка, в отличие от критерия Рауса. Применяя частотный критерий Найквиста и критерий Михайлова, характеристические кривые можно строить постепенно, с учетом влияния каждого звена, что придает критериям наглядность и решает задачу выбора параметров системы из условия устойчивости.
Оценим устойчивость разомкнутой системы по критерию Ляпунова.
Передаточная функция разомкнутой системы
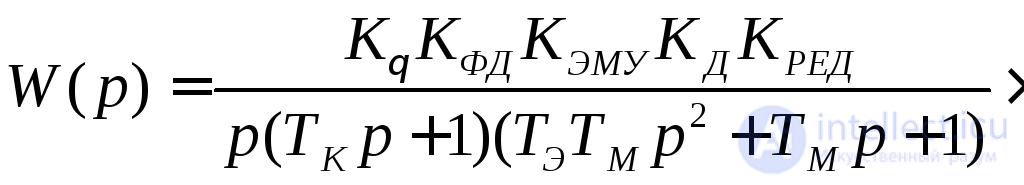
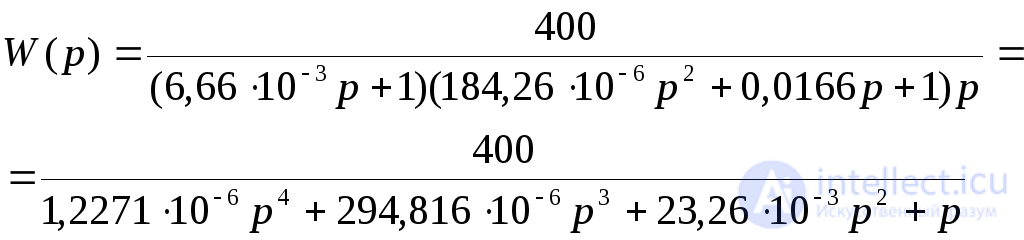
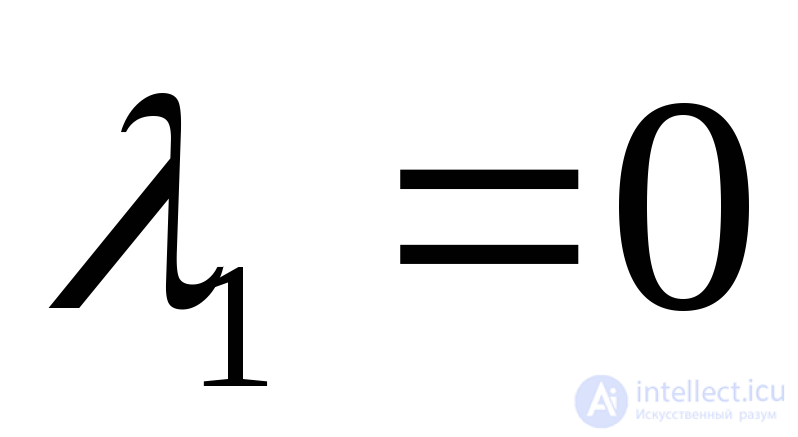
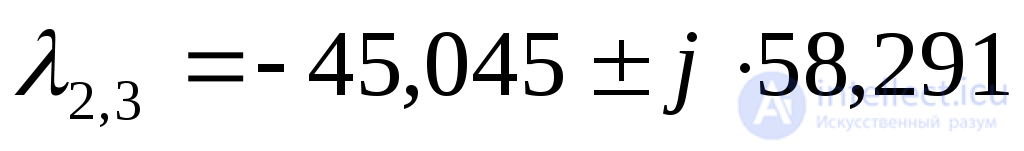
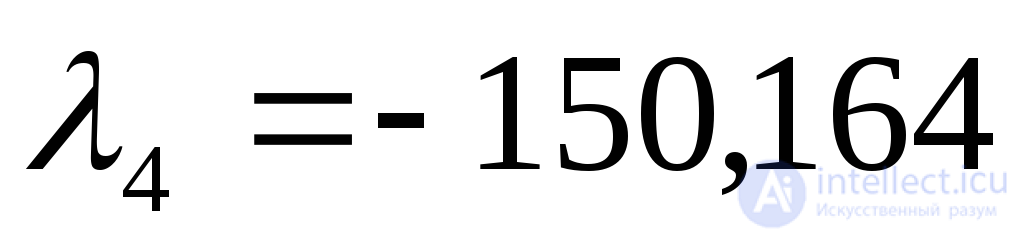
Согласно критерию Ляпунова разомкнутая САУ является устойчивой, причем, поскольку все корни являются действительными отрицательными, а два из них комплексно-сопряженными с отрицательной действительной частью, то переходный процесс представляет собой сходящиеся колебания.
Построим КЧХ разомкнутой системы 
.
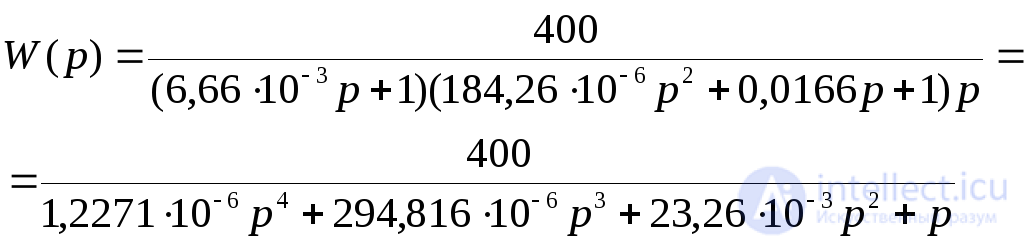
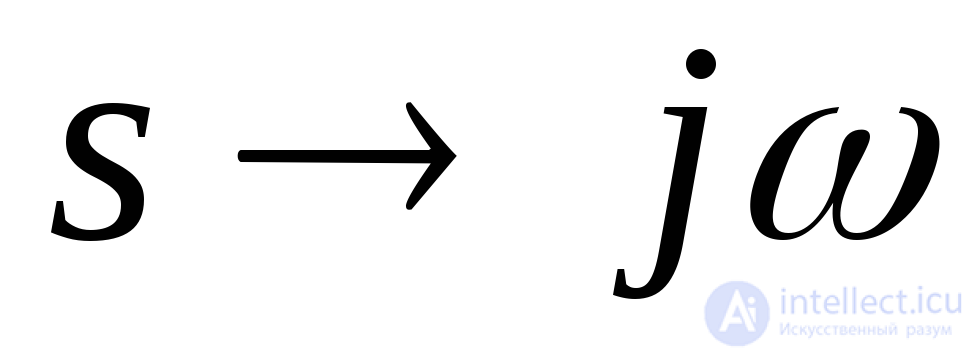
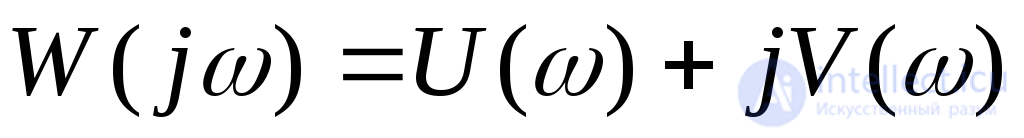
Для исследования устойчивости САУ по критерию Найквиста необходимо построить комплексно-частотную характеристику (КЧХ) исходной разомкнутой САУ и проанализировать ее в соответствии с критерием Найквиста. В случае устойчивой САУ необходимо определить запасы устойчивости по фазе и амплитуде.
Разомкнутая система находится в безразличном состоянии (т.к. эта система астатического класса). Следовательно, критерий устойчивости Найквиста будет выражаться так: чтобы система являлась устойчивой в замкнутом состоянии необходимо и достаточно, чтобы КЧХ разомкнутой системы, дополненная дугой окружности бесконечно большого радиуса, при изменении частоты от нуля до бесконечности не охватывала точку (-1;j0).
Построим КЧХ разомкнутой системы (Рис.5).
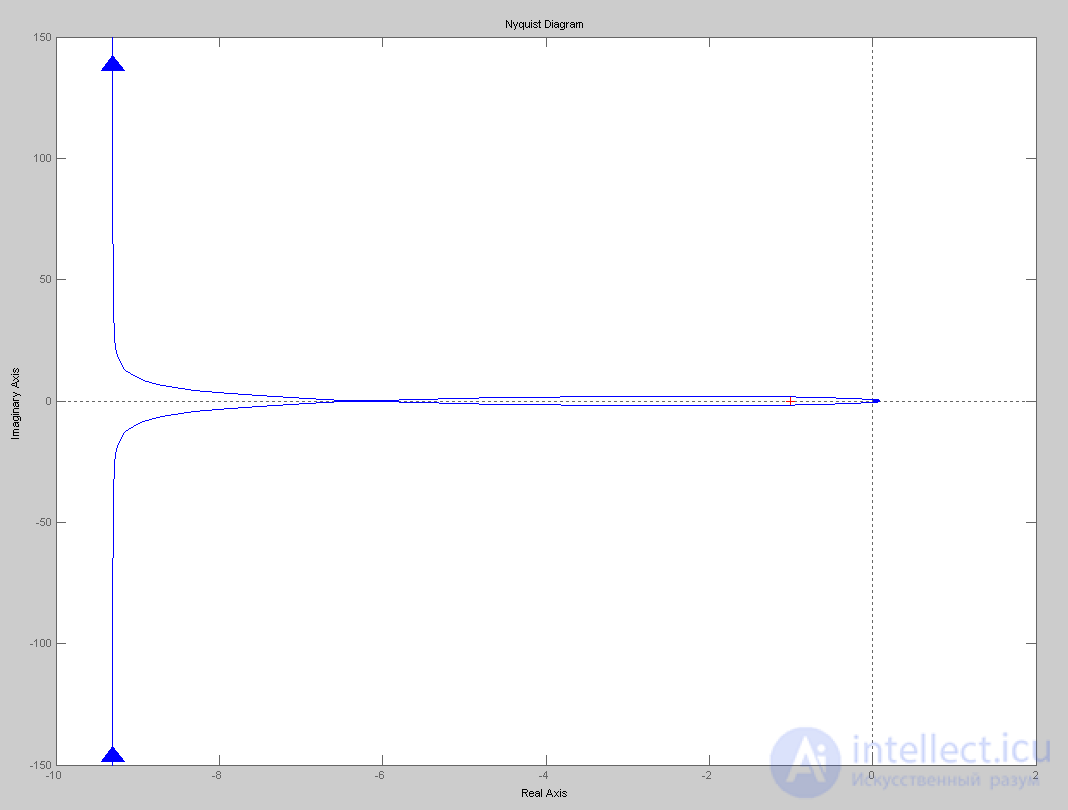
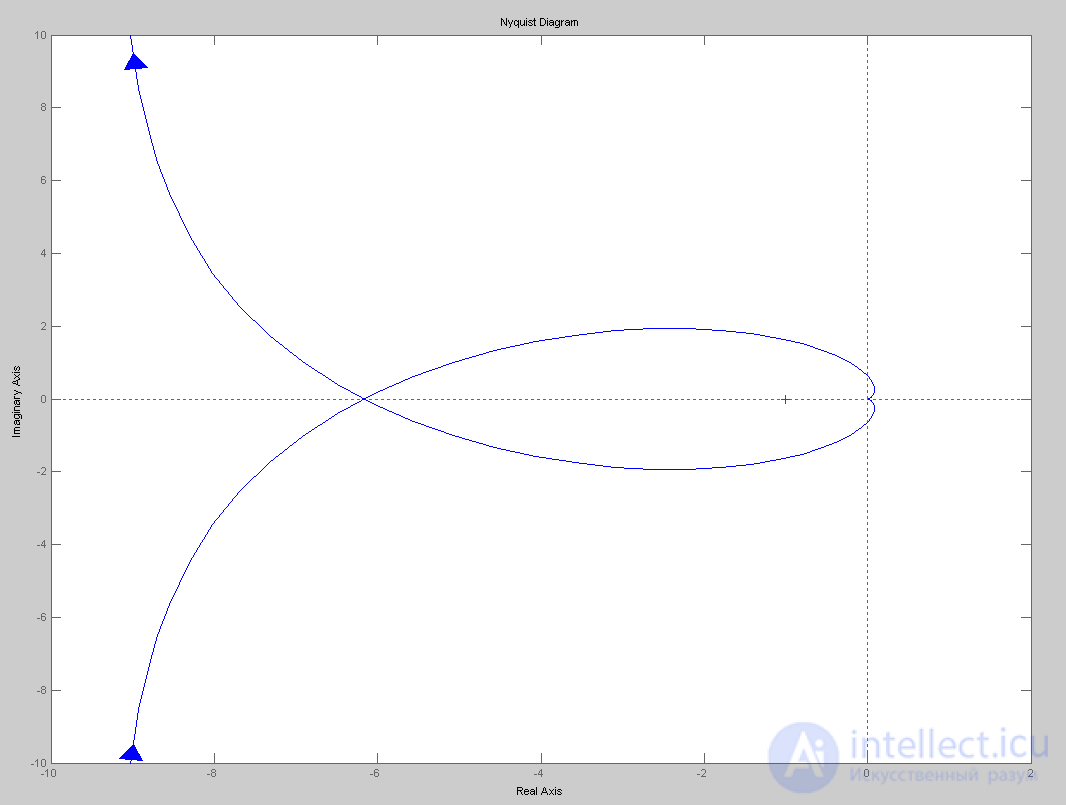
Рис.5. КЧХ разомкнутой системы
Как видно, КЧХ разомкнутой системы охватывает точку (-1;j0). Следовательно, замкнутая система неустойчива.
Пример 1. Передаточная функция системы имеет вид:
.
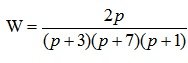Проверить систему на устойчивость. Исследовать устойчивость системы с помощью критерия Гурвица.
Решение:
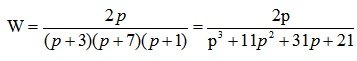
Характеристическое уравнение системы имеет вид:
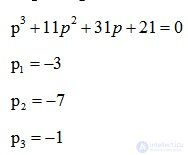
Необходимое условие устойчивости системы автоматического управления: все корни характеристического уравнения должны быть левыми (располагаться во второй или третьей четвертях координатной плоскости). В данном случае необходимое условие выполняется.
Исследование устойчивости системы с помощью критерия Гурвица:
Составим определители Гурвица:
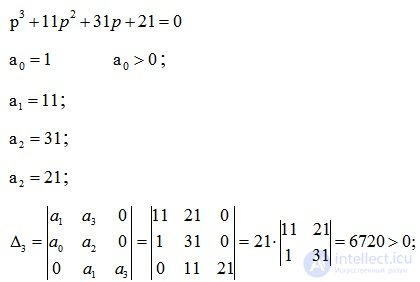
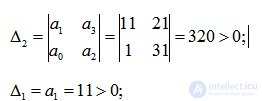
Все определители Гурвица больше нуля, следовательно система устойчива.
Пример 2. Определить устойчивость системы, представленной на рис. 6.12 с помощью критериев Найквиста и Михайлова.
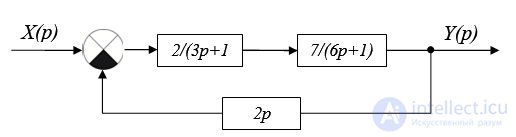
Рис. 6.12. Структурная схема
Решение:
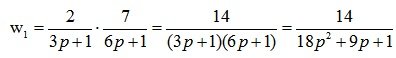
Находим корни характеристического уравнения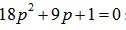 
:
p1=-1/6;
p2=-1/3;
Оба корня лежат по левую сторону от мнимой оси, значит разомкнутая система устойчива.
Критерий Найквиста:
Строим АФЧХ разомкнутой системы (рис. 6.13).
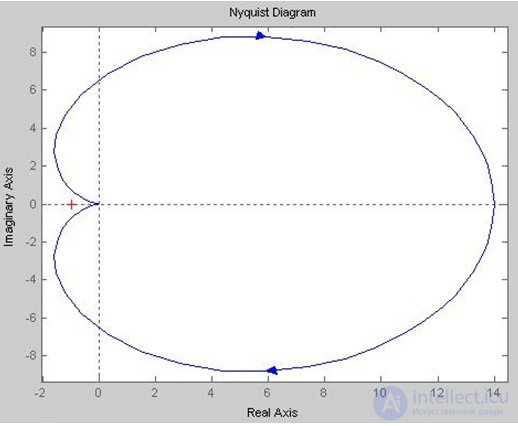
Рис. 6.13. АФЧХ
Вывод: чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w от нуля до бесконечности не охватывала точку с координатами (-1; j0). На рис. 6.13 видно, что система не охватывает точку (-1; j0), значит система является устойчивой.
Критерий Михайлова:
Берем характеристическое уравнение системы:
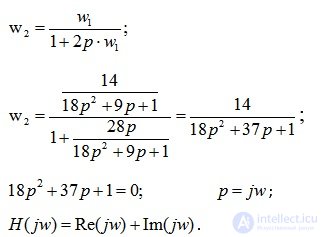
На комплексной плоскости график мнимой части (Im) от реальной (Re) вектора H(jw) опишет при изменении w от 0 до ? кривую – годограф Михайлова (рис. 6.14).
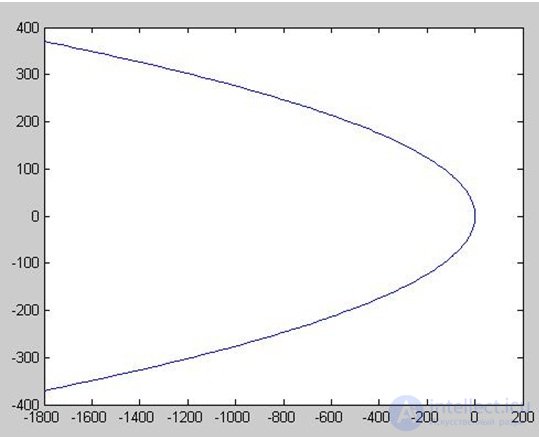
Рис. 6.14. Годограф Михайлова
Вывод:
Для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении w от 0 до ? вектор Михайлова D(jw) повернулся на угол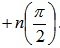 
.
Полученный график соответствует устойчивому состоянию системы (рис. 6.7), так как при изменении w от 0 до ? вектор Михайлова повернулся на угол 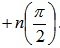. В данном случае n=2 (порядок характеристического уравнения).
Пример 3. Колебательное звено с передаточной функцией
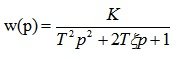
охвачено отрицательной обратной связью через интегрирующее звено (рис. 6.15). Определить устойчивость системы с помощью критериев Найквиста и Михайлова при следующих условиях:
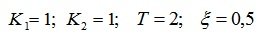
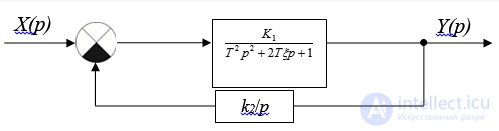
Рис. 6.15. Структурная схема
Решение:
Передаточная функция системы:
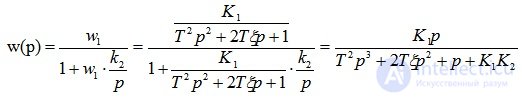
Подставляем значения из условия задачи, получаем:
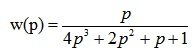
Критерий Найквиста:
Берем передаточную функцию разомкнутой системы , строим график АФЧХ (рис. 6.16).
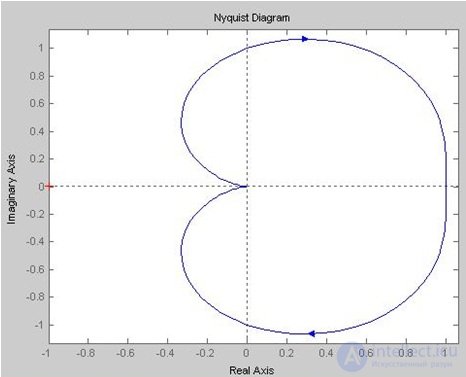
Рис. 6.16. АФЧХ
Вывод: чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w от нуля до бесконечности не охватывала точку с координатами (-1; j0). На рис. 6.16 видно, что система не охватывает точку (-1; j0), значит система является устойчивой.
Критерий Михайлова:
Запишем характеристическое уравнение системы:
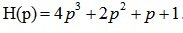
Вводим функцию комплексной переменной, заменяя p на p=j?. Получаем:
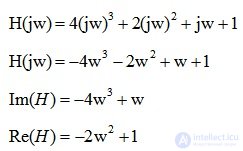
На комплексной плоскости график мнимой части (Im) от реальной (Re) вектора H(jw) опишет при изменении w от 0 до ? кривую – годограф Михайлова (рис. 6.17).
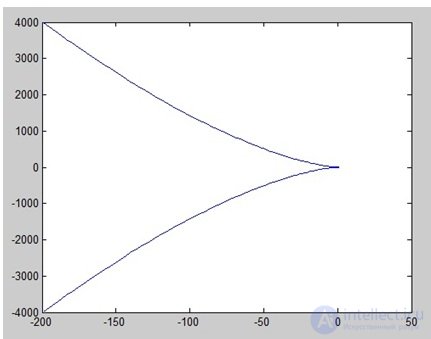
Рис. 6.17. Годограф Михайлова
Вывод: для того, чтобы замкнутая система была устойчивой, необходимо т достаточно, чтобы при изменении w от 0 до ? вектор Михайлова D(jw) повернулся на угол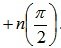 
.
Полученный график соответствует неустойчивому состоянию системы (рис. 6.7).
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления