Привет, Вы узнаете о том , что такое метод пространства состояний, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод пространства состояний, состояние системы , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

состояние системы  – это совокупность таких переменных, знание которых позволяет, при известном входе и известных уравнениях динамики, описать будущее состояние системы и значение ее выхода. Выбор переменных состояния неоднозначен.

метод пространства состояний достаточно универсален, его можно применять для нелинейных систем многомерных систем. Для начального знакомства с этим подходом ниже рассматриваются линейные одномерные системы (или SISO – Single Input Single Output), уравнения состояний которых имеют следующий общий вид:

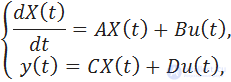
где X(t) – вектор-столбец состояния [n Ч 1]; А – матрица коэффициентов объекта [n Ч n]; В – матрица входа [n Ч 1]; u(t) – сигнал управления; Y – вектор выхода [k Ч 1]; С – матрица выхода [1 Ч n]; D –матрица влияния входа непосредственно на выход системы [n Ч 1](часто полагают D = 0).

 

Уравнения состояния SISO-системы в развернутом виде:

 

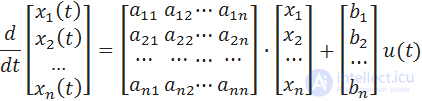
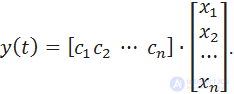
Система, описываемая матрицами А и В, является управляемой,если существует такое неограниченное управление u(t), которое может перевести объект из начального состояния X(0) в любое другоесостояние X(t).

Для SISO-системы с одним входом и одним выходом вводитсяпонятие матрицы управляемости (размером  ):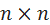

Если детерминант этой матрицы отличен от нуля, то система управляема.

Модальный синтез предполагает формирование таких обратных связей по состоянию, при которых обеспечивается заданное расположениеполюсов замкнутой системы. Модой называется составляющая решения дифференциального уравнения, соответствующая конкретномуполюсу.

Расположение полюсов в основном определяет характер переходного процесса в системе. Обычно рассматриваются такие корневые оценкикачества переходного процесса, как время переходного процесса, степень устойчивости, колебательность и перегулирование.

Для оценки быстродействия системы используется понятие степениустойчивости 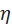 , под которой понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (потому что корни,имеющие наименьшую по модулю вещественную часть, дают в переходном процессе наиболее медленно затухающую составляющую).

Время переходного процесса t можно приближенно оценить по формуле

Запас устойчивости системы оценивается колебательностью. Об этом говорит сайт https://intellect.icu . Система имеет склонность к колебаниям, если характеристическое уравнение содержит комплексные корни  .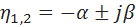

Колебательность оценивается по формуле

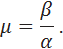
По значению колебательности можно оценить перерегулирование

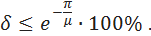
Для объекта, заданного уравнениями состояния (1), управление посостоянию описывается выражением

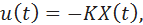
где К – вектор коэффициентов обратной связи.

 

Таким образом, система, замкнутая регулятором, приводится к следующему виду:

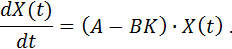
Этому выражению соответствует рис. 1, где g(t) – задающее воздействие.

Основная теорема модального управления гласит, что если линейная динамическая система (8.1) является управляемой, то линейнаяобратная связь может быть выбрана таким образом, что матрица (А-ВK) будет иметь желаемое расположение корней (спектр). При доказательстве этой теоремы используется каноническая форма управляемости матриц A и B.

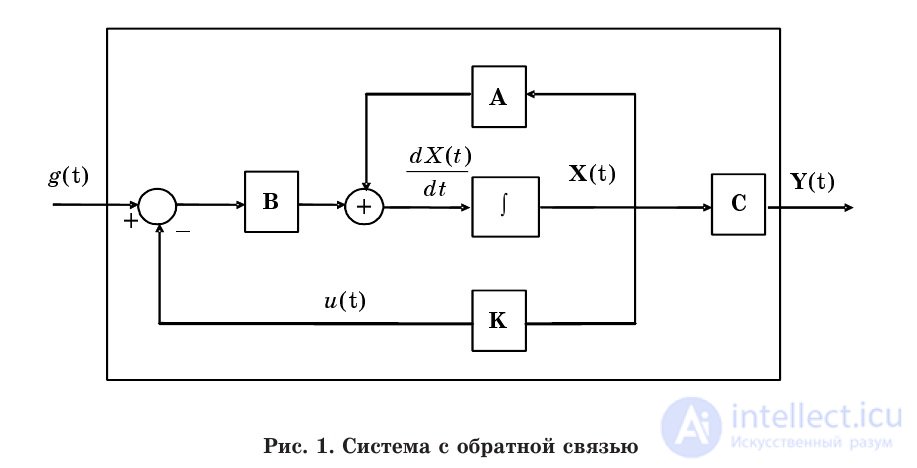
Рис. 6.1. Система с обратной связью

Аккерманом была предложена формула, позволяющая с помощьюпреобразования подобия перевести модель произвольной структуры вканоническую форму управляемости, определить искомые коэффициенты К, а затем пересчитать полученное решение применительно к исходной структуре. Формула Аккермана имеет вид [3]

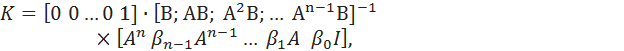
где B – коэффициенты характеристического полинома матрицы (А– ВK).

Таким образом, задача модального синтеза сводится к выбору желаемых корней характеристического полинома замкнутой системы,при которых обеспечиваются заданные параметры переходного процесса, после чего в соответствии со стандартным алгоритмом рассчитываются коэффициенты обратных связей по состоянию.

 

ИспользованиеMatLab

 

>> w1 = ss(A, B, C, D),

 

где A, B, C, D– матрицы модели.

 

Из модели в пространстве состояний можно получить ПФ команnдой:

>> w2 = tf(w1)

 

И, наоборот, если уже существует модель, заданная ПФ, то ее можnно преобразовать в пространство состояний с помощью команды ss:

>> w=tf([2 2],[3 4 1]);

>> w1=ss(w)

Заметим, что одной и той же ПФ могут, вообще говоря, соответnствовать разные модели в пространстве состояний, но всем этим моделям соответствует одна и та же ПФ.

Матрица управляемости может быть построена с помощью функnции ctrb, которая вызывается одной из команд:

>> W = ctrb(A, B)

>> W = ctrb(sys)

>> W = ctrb(sys.A, sys.B)

 

В пакете MatLab имеется функция acker, с помощью которой можно обеспечить желаемое расположение полюсов одномерной линейной системы (в соответствии с формулой Аккермана):

>> k = acker(A,B,P),

 

где А и В – матрицы системы; Р – вектор, задающий желаемое распоnложение полюсов системы.

Пример. Пусть система описывается матрицами

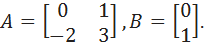
Желаемые полюса заданы вектором:

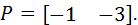
Тогда рассчитать значение коэффициентов обратных связей можно с помощью команд

>>A=[0 1;,2 3];

>> B=[0; 1];

>> P=[,1 ,3];

>> K=acker(A,B,P)

K =1 7

Таким образом, управление в этом примере должно быть сформировано в виде

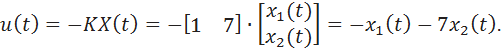
Для многомерных систем в пакете MatLab имеется функция place(ее можно использовать также и для одномерных систем). Функция

>> K=place(A,B,P)

 

рассчитывает матрицу коэффициентов обратных связей K, которая обеспечивает желаемое расположение полюсов системы. Длинавектора Pдолжна быть равна числу строк матрицы А.

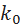Следует заметить, что метод модального управления не гарантирует равенство установившейся ошибки нулю. Для обеспечения равенства задающего воздействия и выходного сигнала системы в установившемся режиме вводится масштабирующий коэффициент  . Дляего вычисления запишем уравнения состояния в виде: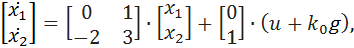

подставляя уравнение (6), имеем:

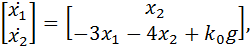
В установившемся режиме получаем

и должно выполняться условие

Следовательно, из уравнения (7) получаем

На этот коэффициент должно умножаться входное воздействие.

 

В пакете моделирования Simulink MatLab для описания объекта в пространстве состояний имеется блок State Space. Однако этот блок не позволяет непосредственно оценивать текущее значение вектора состояния, поэтому для моделирования работы модального регулятор нужно детально описывать матричные операции.

Прочтение данной статьи про метод пространства состояний позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое метод пространства состояний, состояние системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про метод пространства состояний