2.4 Построение моделей системы управления вход-выход кратко

Привет, Вы узнаете о том , что такое построение моделей системы управления вход-выход, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое построение моделей системы управления вход-выход , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Модель вход-выход системы управления строится по известным уравнениям отдельных компонентов (блоков, звеньев, см. п.4.1). Процедура сводится к преобразованию системы дифференциальных уравнений, описывающих поведение отдельных блоков, к единому уравнению системы управления вида [М1], [М2] или [М3]. При этом вне зависимости от первоначального описания наиболее удобной для осуществления подобных преобразований является операторная форма [M3], которая по окончанию процедуры может быть легко приведена к виду [М1] или [М2].

2.4.1. Простейшие соединения блоков. Рассмотрим последовательное соединение блоков, т.е. систему, состоящую из блоков Б1 и Б2 и описываемую операторными уравнениями:

(2.82) ,

(2.83) ,

где, соответственно, - выходной, а - входной сигналы системы.

Рис. 2.18. Последовательное соединение блоков

Требуется найти единое описание системы (2.82)- (2.83) , т.е уравнение связи сигналов и . Подставляя (2.83) в (2.82) получаем

(2.84) .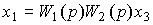

Таким образом система описывается уравнением

(2.85) ,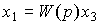

где - передаточная функция системы последовательно соединенных блоков.

Пример 2.4. Рассмотрим последовательное соединение апериодического звена (с единичным коэффициентом передачи) и идеального дифференцирующего звена (см. п.2.3). Применение рассмотренного выше правила дает передаточную функцию

(2.86) ,

которая совпадает с передаточной функцией реального дифференцирующего звена.

Рассмотрим параллельное соединение тех же блоков, т.е. систему описываемую уравнениями

(2.87) ,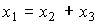

(2.88) ,

(2.89) ,

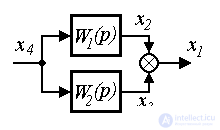
Рис. 2.19. Параллельное соединение блоков

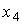где - выходной, а - входной сигналы системы. После соответствующих подстановок находим связь выхода и входа:

(2.90) ,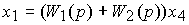

или

(2.91)

где - передаточная функция системы параллельно соединенных блоков.

Пример 2.5. Рассмотрим параллельное соединение пропорционального и интегрирующего звеньев (ПИ-регулятор, см. Об этом говорит сайт https://intellect.icu . п. 4). Используя полученное выше правило находим передаточную функцию звена, называемого изодромом:

(2.92) .

Рассмотрим систему, составленную из двух блоков, один из которых подключен к другому в виде отрицательной обратной связи (подключение в обратную связь), т.е.

(2.93) ,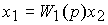

(2.94) ,

(2.95) ,

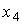где - выходной, а входной - сигнал системы.

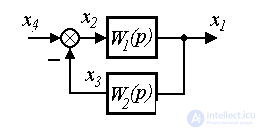
Рис. 2.20. Подключение в обратную связь

После элементарных преобразований, получаем

(2.96) .

Таким образом система описывается уравнением вида (2.96) и имеет передаточную функцию

(2.97) .

Пример 2.6. Рассмотрим двойной интегратор, имеющий передаточную функцию

,

с отрицательной обратной связью, образованной пропорциональным звеном с коэффициентом 2. Используя формулу (2.96) находим

,

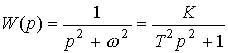где K=1/ 2 , T=1/ , т.е. составной блок является консервативным звеном (см. п. 2.5).

Пример 2.7. Рассмотрим последовательное соединение пропорционального звена с коэффициентом b и интегратора с отрицательной обратной связью в виде пропорционального блока с коэффициентом a. Используя рассмотренные выше правила находим

(2.98) ,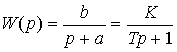

где a=K/T, b=1/K. Полученная передаточная функция соответствует апериодическому звену (см. п. 2.3).

Отметим, что для системы с положительной обратной связью, уравнение (2.95) принимает вид

(2.99)

и

(2.100) .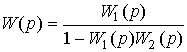

С другой стороны, в простейшем частном случае (единичная отрицательная обратная связь) 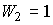и, следовательно,

(2.101) .

2.4.2. Передаточные функции систем управления. Сначала рассмотрим систему управления без обратной связи (так называемую разомкнутую систему, см. п.4.3), состоящую из последовательно соединенных регулятора и объекта управления. Пусть объект управления описывается операторным уравнением

(2.102) ,

а регулятор представлен выражением

(2.103) ,

Рис. 2.21. Разомкнутая система

где y(t) - выходная переменная, u(t) - управляющее воздействие, y*(t) - задающее воздействие (вход системы), W0 (p) и K(p) - передаточные функции (интергро-дифференциальные операторы). Используя правило построения модели последовательно соединенных блоков, находим уравнение

(2.104) ,

связывающее выходную переменную y(t) и входную переменную y*(t) через передаточную функцию разомкнутой системы

(2.105) .

Передаточная функция может быть записана в виде

(2.106) ,

где a(p), b(p) - дифференциальные операторы соответствующих степеней. Тогда уравнение (2.104) можно привести к виду

(2.107)

и при необходимости переписать в стандартной форме [М1].

Теперь рассмотрим замкнутую систему управления, т.е. систему, представленную объектом управления (2.102) и простейшим регулятором отклонения (см. п.1.5):

(2.108) u(t)=K(p)e (t),

(2.109) e (t) = y*(t)- y(t),

где e - рассогласование (ошибка). Используя правило (2.96) находим модель замкнутой системы в виде

(2.110) ,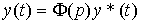

Рис. 2.22. Замкнутая система

где (p) - передаточная функция замкнутой системы, определяемая как

(2.111) .

Учитывая (2.106) нетрудно получить

(2.112) .

Сравнение последнего выражения с (2.106) показывает, что замыкание системы приводит к изменению знаменателя ее передаточной функции a(p)+b(p), т.е. характеристического полинома системы.

Прочтение данной статьи про построение моделей системы управления вход-выход позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое построение моделей системы управления вход-выход и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про построение моделей системы управления вход-выход