3.3 Фазовые траектории автономной системы второго порядка

Привет, Вы узнаете о том , что такое фазовые траектории автономной системы второго порядка, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое фазовые траектории автономной системы второго порядка , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Рассмотрим автономную систему второго порядка:

(3.74)                      ,

с начальными значениями 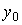 ,  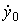. Характеристическое уравнение системы

(3.75)                     

имеет два вещественных или комплесно-сопряженных корня (полюса системы):

(3.76)                      ,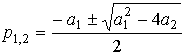

расположение которых на комплексной плоскости определяет вид переходных процессов

(3.77)                     y=y(y₀, 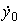 , t)

и динамические свойства системы (см. п. 1.4.1).

Определим переменные состояния, как фазовые переменные: 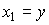 ,  . Модель состояние-выход принимает вид:

(3.78)                      ,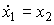

(3.79)                      ,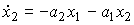

(3.80)                      ,

с начальными значениями  ,  Собственные числа матрицы системы

                    

совпадают с корнями характеристического полинома (3.75) p_1,2.

Собственные векторы 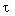 _1,2 (см. п. 3.1.3) рассматриваемой системы второго порядка находятся (при условии вещественности ее полюсов) из выражения

                     ,

т.е.

                    

и соответствующие собственные подпространства R_1,2 представлены прямыми

(3.81)                     x₂ =p_1,2 x₁.

Равновесные (установившиеся) состояния ( x₁*, x₂* ) системы (3.78), (3.79), (3.80) находятся из условия

(3.82)                      ,  .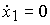

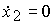При a ₂ 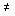 0 получаем, что положением равновесия является начало координат

(3.83)                     x₁*=0, x₂*=0,

а при a₂ = 0 находим множество равновесных состояний (прямую)

(3.84)                     x₂ =0.

Напомним, что интегральной кривой (фазовой траекторией) рассматриваемой системы является годограф вектора состояния  = при изменении параметра t, а множество фазовых траекторий, полученных для различных начальных условий, образуют ее фазовый портрет (см. п. 3.1.2).Фазовые траектории могут быть получены экспериментально или найдены аналитическим путем. В последнем случае используется следующий прием. Уравнения (3.78), (3.79) записываются в виде

                    dx₁=x₂ dt,

                    dx₂= - (a₂ x₁ +a₁ x₂) dt.

После деление второго выражения на первое получаем дифференциальное уравнение

(3.85)                      .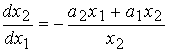

Решение этого уравнения ищется в виде

(3.86)                     x₂=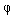 ₁ (x₁)

и определяет интегральную (фазовую) траекторию рассматриваемой

системы на плоскости R².

Рассмотрим переходные процессы, соответствующие различным значениям корней характеристического уравнения (полюсов системы (3.78) - (3.80)).

1. Об этом говорит сайт https://intellect.icu . Для неравных вещественных корней (рис. 3.4, 3.5)

(3.87)                     p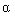_1,2= _1,2=

уравнение (3.74) имеет решение

(3.88)                      ,

что соответствует апериодическому процессу (см. п. 2.2.2).

При условии, что a₁ >0 и a₂>0,

                    Re p_1,2=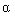 _1,2<0,

(рис. 3.4). В этом случае имеет место затухающий переходный процесс, выполняется условие

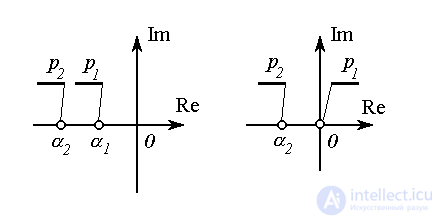
Рис. 3.4                     

Рис. 3.5

(3.89)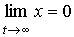                     

и фазовые траектории системы при t 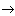  сходятся к положению равновесия O (рис. 3.6), которое называется устойчивым узлом. (Система такого рода относится к классу асимпототически устойчивых систем [11,12] ). Система имеет два собственных (инвариантных) подпространства R₁ и R₂, на которых решения уравнения (3.74) записываются как

 

Рис. 3.6                     

Рис. 3.7

(3.90)                     

и

(3.91)                      ,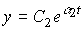

т.е. динамика на собственных подпространствах соответствует поведению системы первого порядка.

При условии, что a₁ >0 и a₂ =0, получаем

                    Re p₁=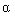 <0, p₂=0,

(рис. 3.5 ). Фазовые траектории системы (рис. 3. 7 ) при t   сходятся к множеству равновесных состояний (прямой R₀ ), описываемому уравнением (3.84). Это же множество является собственным подпространством системы. (Система такого рода относится к классу устойчивых, или нейтрально устойчивых, систем, см. [10,12])

При условии, что a₁ <0 и a₂>0,

                    Re p₁=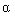 ₁>0, Re p₂=  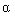₂<0,

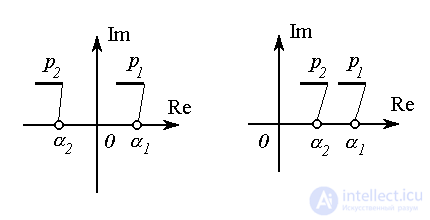
Рис. 3.8                     Рис. 3.9

(рис. 3.8). В этом случае имеет место расходящийся переходный процесс. Фазовые траектории системы при t   расходятся (рис. 3.10):

(3.92)                     

за исключением траекторий, начинающихся на прямой R₂ , для которых выполняется предельное соотношение (3.89).(Система такого рода относится к классу неустойчивых систем, см. [10,12] ) Положение равновесия системы (точка O ) называется седловой точкой (седлом). Система имеет два собственных (инвариантных) подпространства R₁ и R₂ , на которых решения (3.74) записываются в виде (3.90) или (3.91) .

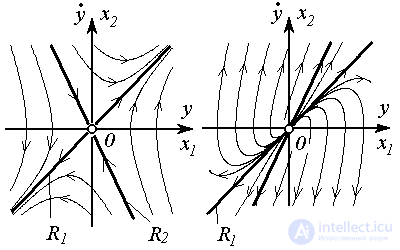
Рис. 3.10                     Рис. 3.11

При условии, что a₁ <0 и a₂<0,

                    Re p₁=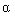 ₁>0, Re p₂=  ₂>0,

(рис. 3.9). В этом случае имеет место расходящийся переходный процесс и все фазовые траектории (рис. 3.11) системы при t   расходятся (выполняется (3.92)). Положение равновесия системы (точка O ) называется неустойчивым узлом (и система также неустойчива). Система также имеет два собственных (инвариантных) подпространства R₁ и R₂.

2. Если  , то система имеет равные вещественные полюсы (рис. 3.12 - 3.14)

                    p_1,2= =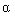

и решение уравнения (3.74) принимает вид:

 

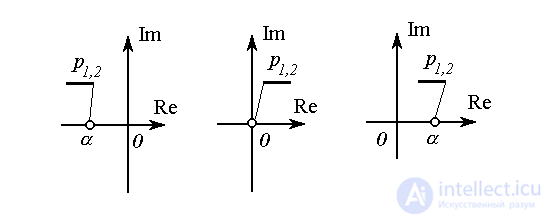
Рис. 3.12                     Рис. 3.13                     Рис. 3.14

                    y=(C₁+C₂t) ,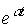

соответствующее апериодическому процессу (см. п. 2.2.2 ).

При условии, что a₂ >0 (и a₁>0),

                    Re p_1,2=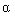 <0,

Рис. 3.15                     Рис. 3.16                     Рис. 3.17

(рис. 3.12). В этом случае имеет место затухающий переходный процесс, выполняется предельное соотношение (3.89), фазовые траектории при t  сходятся к положению равновесия (устойчивому узлу) O (рис. 3.15) и система асимптотически устойчива. Собственные подпространства системы R₁ и R₂совпадают.

При условии, что a₁=a₂ =0, получаем

                    p₁= p₂=0,

(рис. 3.13) и расходящийся переходный процесс. Фазовые траектории системы (рис. 3.16) при t   уходят в бесконечность, за исключением траекторий, начинающихся на множестве равновесных состояний (прямой R₀ ), описываемом уравнением x₂ = const , и система неустойчива.

При условии, что a₂ <0 и a₁ <0, выполняется

                    Re p_1,2=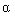 >0,

рис. 3.12),. собственные подпространства системы совпадают. В этом случае имеет место предельное соотношение (3.89), фазовые траектории при t  расходятся. Положение равновесия O является неустойчивым узлом O (рис. 3.17 ) и система неустойчива.

3 . Если выполняется  , то система имеет комплексно-сопряженные полюсы (рис. 3.18-3.20 )

                     

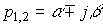
Рис. 3.18                     Рис. 3.19                     Рис. 3.20

а решения уравнения (3.74) принимают вид

                    

что соответствует колебательному процессу (см. п. 2.2.2).

Рассматриваемая здесь система с комплексными полюсами не имеет собственных подпространств.

При условии, что a₁ >0 и a₂>0,

                    Re p_1,2=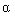 <0,

(рис. 3.18 ). В этом случае имеет место затухающий колебательный переходный процесс. Выполняется ( 3.89 ), фазовые траектории системы при t 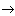 сходятся к положению равновесия O (рис. 3.21 ), которое называется устойчивым фокусом, и система асимптотически устойчива.

При условии, что a₂=0, Re p_1,2=0, система имеет чисто мнимые корни

                    p_1,2 = - j

(рис. 3.22 ) и называется линейным осциллятором (см. п. 2.3). В этом случае имеет место незатухающий колебательный процесс. Фазовые траектории системы представлены замкнутыми концентрическими кривыми ( эллиптическими орбитами ) , и система (нейтрально) устойчива. Положение равновесия системы (точка O ) называется центром

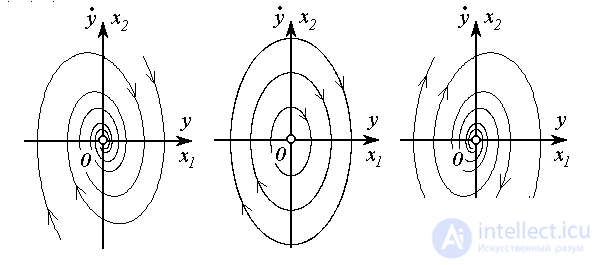
Рис. 3.21                     Рис. 3.22                     Рис. 3.23

При условии, что a₁ < 0 и a₂ < 0,

                    Re p_1,2= >0,

(рис. 3.20). В этом случае имеет место расходящийся колебательный переходный процесс. Фазовые траектории системы при t   расходятся от положения равновесия O (рис. 3.23), которое называется неустойчивым фокусом, и система неустойчива.

Прочтение данной статьи про фазовые траектории автономной системы второго порядка позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое фазовые траектории автономной системы второго порядка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления