4.2 Модели задающих блоков и внешних воздействий

Привет, Вы узнаете о том , что такое модели задающих блоков, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое модели задающих блоков, внешних воздействий , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Для описания внешней среды, объектов слежения и генерации задающих воздействий в системах программного управления возникает необходимость в конструировании дополнительных динамических моделей (генераторов внешних воздействий ), выходом которых является возмущающее 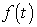 или задающее y*(t) воздействие (см. п. 1.2.1). Для гладких функций  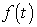и y*(t ) соответствующие генераторы возмущающих и задающих воздействий (задающие блоки) могут быть получены в классе автономных линейных моделей, аналогичных рассмотренным ранее моделям [М1а], [М2а] или [ М6а], [М7]

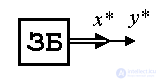
Так, задающий блок ЗБ (генератор задающих воздействий) может быть описан однородным дифференциальным уравнением вида

(4.24)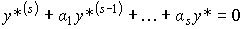                     

с постоянными коэффициентами 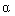 _i и начальными значениями

(4.25)                      ,  ,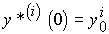

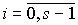или соответствующими векторно-матричными уравнениями состояния

(4.26)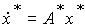                     

и выхода

(4.27)                      ,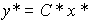

где 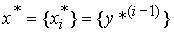 - s - мерный вектор заданий (состояния генератора) с начальными значениями координат  .

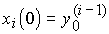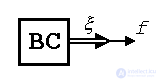
Генератор гладких возмущающих воздействий (модель внешней среды ВС) описывается однородным уравнением

(4.28)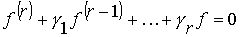                     

с постоянными коэффициентами 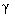 _i и начальными значениями

(4.29)                      ,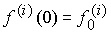 

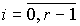
или в компактной форме

(4.30)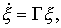                     

(4.31)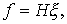                     

где 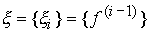 - r - мерный вектор состояния внешней среды с начальными значениями координат  .

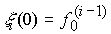Воздействия, генерируемые рассмотренными моделями, соответствуют решениям дифференциальных уравнений (4.26), (4.27) и (4.30), (4.31), т.е. функциям

(4.32)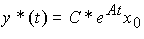                     

и

(4.33)                      ,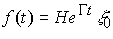

соответственно. В частных случая с помощью таких моделей могут быть получены:

• полиномиальные воздействия

(4.34)                      ,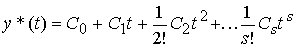

где 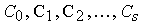 - постоянные, определяемые как

(4.35)                      ;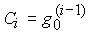

• гармонические воздействия

(4.36)                      ,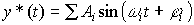

где А _i , 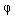 _i и 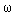 _i - постоянные, соответствующие амплитудам, фазам и частотам гармоник и т.д.

Для построения модели воздействия по заданной функции y*(t ) (или 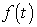 ) можно воспользоваться методом последовательного дифференцирования соответствующих аналитических выражений

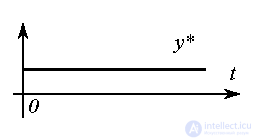
(4.37)                     y=y*(t)

(или f=f(t) ), представленных, например, в виде (4.34) или (4.36).

Пример 4.1. Об этом говорит сайт https://intellect.icu . Для получения модели постоянного сигнала

(4.38)                     y*(t)=С ₀,

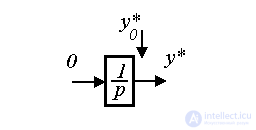
продифференцируем последнее выражение по времени. Получим уравнение первого порядка

(4.39)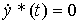                     

с начальным значением y*(0)=С ₀ .

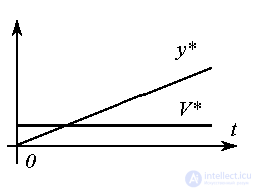
Модель линейно нарастающего сигнала (равномерного движения)

(4.40)                      ,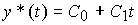

получается двукратным дифференцированием. На первом шаге получаем

(4.41)                      ,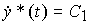

а на втором - искомое дифференциальное уравнение

(4.42)                      .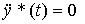

Для получения начальных условий из уравнения (4.40) найдем y*(0) =С ₀ , а из уравнения (4.41) - 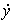 *(0)=С ₁.

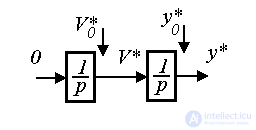
Уравнение (4.42) приводится к форме модели состояния (системе уравнений в форме Коши). Для этого кроме основной переменной состояния, совпадающей с выходной переменной y*(t ), вводится вторая переменная V*(t ) (скорость движения):

(4.43)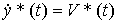                     

с начальным значением 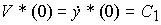 . Уравнение (4.42) можно переписать в виде

(4.44)                      .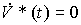

Полученные уравнения (4.43) и (4.44) описывают искомую модель состояния задающего блока.

Отметим, что решение уравнения (4.42) или системы (4.43), (4.44) (т.е. выражение (4.40)) можно записать в виде

(4.45)                      .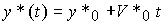

Модель квадратично нарастающего сигнала

(4.46)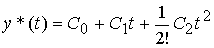                     

(равноускоренного движения) получается в результате процедуры трехкратного дифференцирования выражения (4.46) и имеет вид

(4.47)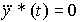                     

с начальными условиями

                   

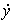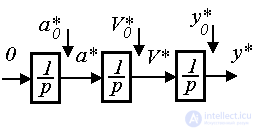
y*(0) =С ₀ ,  *(0) =С ₁ и 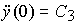 . Для построения модели состояния рассматриваемого задающего блока вводится переменные состояния y*(t), V*(t), a* (t), где  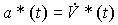- ускорение, и после их дифференцирования по времени и соответствующих подстановок получается система уравнений

(4.48)                      ,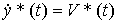

(4.49)                      ,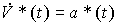

(4.50)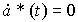                     

с начальными значениями у* (0) =С ₀, V*(0)=C₁, a*(0)=C₂.

Отметим, что решение уравнения (4.47) или системы (4.48), (4.49) (т.е. выражение (4.46)) можно записать в виде

(5.51)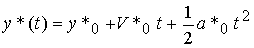                     

 

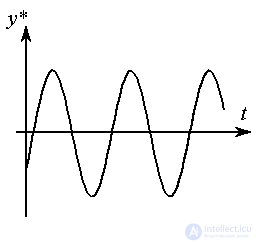
Пример 4.2. Для генерации простейшего гармонического воздействия

с частотой 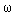 , т.е. сигнала

                     ,

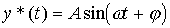используется модель одночастотного линейного осциллятора (консервативного звена, см. п. 2.3):

(4.52)                      .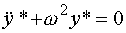

Значения амплитуды колебаний A и фазового сдвига 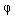 определяются начальными значениями модели y (0) и  .

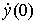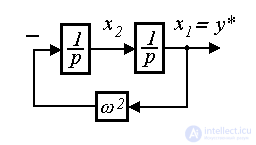
Модель (4.52) легко приводится к форме Коши

(4.53)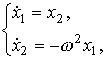                     

с выходом

(4.54)                      .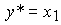

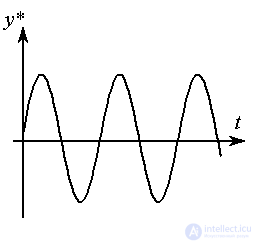
Здесь введены следующие обозначения:

(4.55)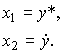                     

В частном случае для построения генератора сигнала

(4.56)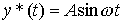                     

вводятся переменные состояния

(4.57)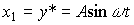                     

(4.58)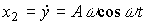                     

с начальными значениями

(4.59)                      ,  .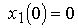

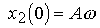После дифференцирования по времени выражений (4.57), (4.58) и соответствующих подстановок получаем систему уравнений (4.53).

Замечание 4.1. Если переменные состояния выбрать как

(4.60)                      ,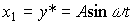

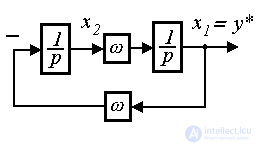
(4.61)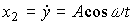                     

с начальными значениями 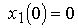 , ,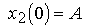 то модель состояния задающего генератора примет вид

(4.62)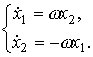                     

Для генерации негладких функций y*(t) и f(t) используются

• нелинейные динамические модели [10];
• модели с переменной структурой [10];
• неавтономные линейные модели вида:

(4.63)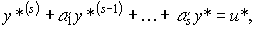                     

где 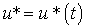 - негладкое (может быть разрывное) входное воздействие модели.

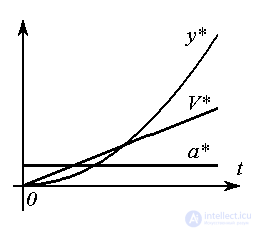
Пример 4.3. Для генерации сигнала y*(t) с трапециидальным графиком скорости 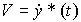 (рис. 4.6) можно воспользоваться моделью:

(4.64)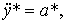                     

 

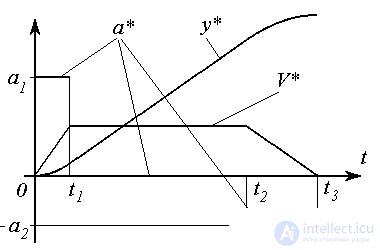
Рис. 4.6. Процессы генератора негладких сигналов

или - в форме Коши

(4.65)                      ,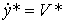

(4.66)                      ,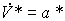

где a*=a*(t ) - сигнал ускорения вида

(4.67)                     

где a₁>0 и a₂>0 - постоянные.

Прочтение данной статьи про модели задающих блоков позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое модели задающих блоков, внешних воздействий и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про модели задающих блоков