2.3 Элементарные звенья

Привет, Вы узнаете о том , что такое элементарные звенья, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое элементарные звенья , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

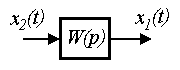
Элементарными звеньями называются простейшие составные части (блоки) системы, поведение которых описывается алгебраическими уравнениями или дифференциальными уравнениями 1-го - 2-го порядка:

(2.50)                      ,

где  - выходная переменная, 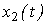 - входная переменная,  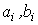- постоянные коэффициенты (параметры). Уравнение (2.50) можно записать в операторной форме:

                     ,

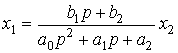т.е. передаточная функция звена имеет вид

(2.51)                       .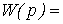

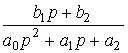Пропорциональное (безинерционное) звено. Звено описывается алгебраическим уравнением

(2.52)                      ,

где  - коэффициент пропорциональности, который (в силу отсутствия у блока инерционных свойств) совпадает со статической характеристикой. Переходная функция пропорционального звена -

(2.53)                      .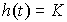

Примеры: измерительные потенциометры, редукторы, усилители напряжения (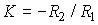 ) и т.д.

Апериодическое звено. Звено описывается дифференциальным уравнением

(2.54)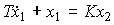                     

или, в приведенной форме - уравнением

(2.55)                      ,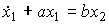

где - коэффициент,  - постоянная времени, a=K/T, b=1/K. Операторная форма звена имеет вид

(2.56)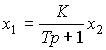                     

или, соответственно,

(2.57)                      ,

Переходная функция звена определяется выражением

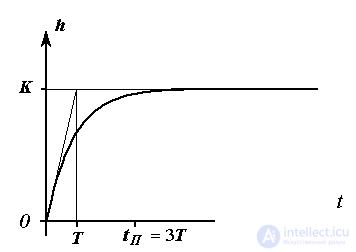
Рис. 2.10. Переходная функция апериодического звена

 

(2.58)                      ,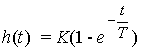

 

а статическая характеристика -

(2.59)                      .

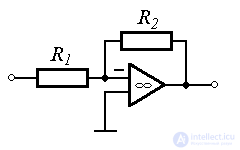
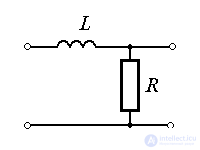
Примеры: усилители мощности, тепловые процессы, процесс разгона двигателя  - цепь (см. пример 1.1), LR цепь.

 

Интегрирующее звено. Звено описывается дифференциальным уравнением

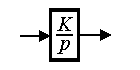
(2.60)                     

или, в операторной форме

(2.61)                      .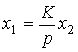

Переходная функция интегрирующего звена

(2.62)                      .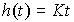

Звено относится к астатическим блокам и поэтому не имеет статической характеристики.

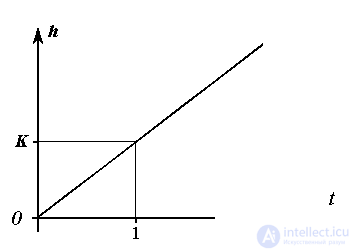
Рис. Об этом говорит сайт https://intellect.icu . 2.11. Переходная функция интегрирующего звена

Примеры: элементы механических систем (см. движение материальной точки, пример 2.3), описываемые уравнениями динамики вида

                   

 ,

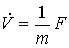и кинематическими уравнениями

                     ;

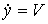электронные интеграторы (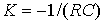 ) и т.д.

 

Дифференцирующее звено (идеальное). Звено описывается дифференциальным уравнением

(2.63)                     

или, в операторной форме,

(2.64)                      .

Переходная функция дифференцирующего звена -

(2.65)                      ,

а реакция звена на линейно-нарастающий сигнал x₂=t -

(2.66)                      .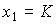

При x₂ = const для любых t>0 выполняется 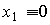 и, следовательно, статической характеристикой звена является прямая  .

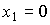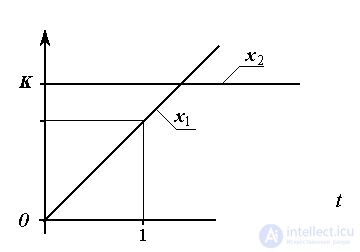
Рис. 2.12. Реакция дифференцирующего звена 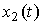 на линейно нарастающее воздействие 

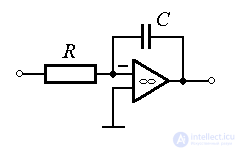
Примеры: тахогенератор (электромашинный датчик скорости), электронный дифференциатор ( ).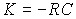

Замечание 2.4. Выходом дифференцирующего звена является производная входного сигнала, т.е. его мгновенная скорость dx₂/dt. Операция нахождения текущего значения скорости x₁(t)=dx₂(t)/dt только по информации об известном в данный момент времени t сигнале x₂(t) физически не реализуема и поэтому идеальных дифференцирующих звеньев не существует. Тем не менее производная может быть приближенно рассчитана как 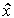 ₁(t)=D x₂(t)/D t, где D t - интервал времени, D x₂ - соответствующее приращение сигнала x₂. При уменьшении интервала D t можно получить значение  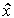₁(t), сколь угодно близкое к текущему значению скорости x₁(t). Следовательно, несмотря на нереализуемость (с абсолютной точностью) операции дифференцирования, теоретически возможно построение звена, которое обеспечивает нахождение производной dx₂(t)/dt со сколь угодно высокой точностью.

Реальное дифференцирующее звено. Звено описывается уравнением

(2.67)                      .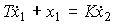

или, в операторной форме,

(2.68)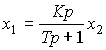                     

Переходная функция звена имеет вид

 

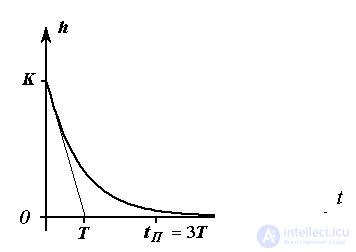
Рис. 2.13. Переходная функция реального дифференцирующего звена

(2.69)                      ,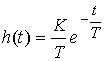

а реакция звена на линейно-нарастающий сигнал x₁=t совпадает с переходной функцией апериодического звена, т.е.

(2.70)                      .

При x₂=const и 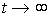 выполняется  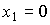, что соответствует статической характеристике звена.

При достаточно малых постоянных времени T, характеристики звена приближаются к характеристикам идеального дифференцирующего звена (см. Замечание 2.4).

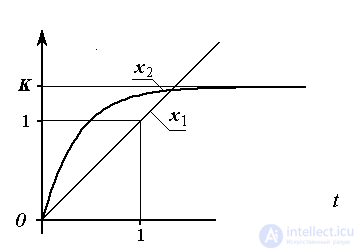
Рис. 2.14. Реакция реального дифференцирующего звена  на линейно нарастающее воздействие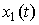 

Примеры: CR и RL цепи.

 

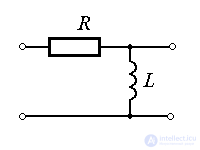
Колебательное звено. Звено описывается дифференциальным уравнением 2-го порядка

(2.71)                      ,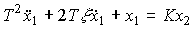

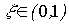 - постоянная времени,  - параметр затухания, или операторным уравнением (2.50), где передаточная функция имеет вид

(2.72)                      .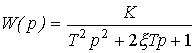

Корни характеристического уравнения принимают значения

                      ,

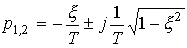
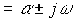где  - коэффициент затухания, 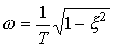 - угловая частота колебаний.

Переходная функция звена имеет вид

(2.73)                      ,

где  ;  , а статическая характеристика -

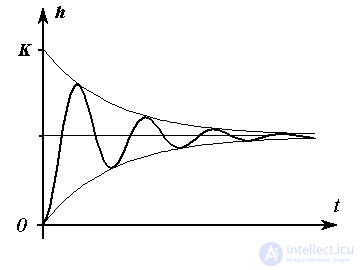
Рис. 2.15. Переходная функция колебательного звена

(2.74)                      .

 

Примеры: маятник в вязкой среде,  - цепь.

Замечание 2.5. В предельном случае при  на выходе звена возникают незатухающие колебания, а при  - монотонный (апериодический) процесс, что соответствует рассматриваемым далее консервативному и двойному апериодическому звену.

Консервативное звено (осциллятор). Звено описывается дифференциальным уравнением

(2.75)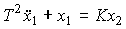                     

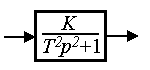
или операторным уравнением (2.50), где

(2.76)                      ,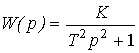

и получается из колебательного звена при  . Консервативное звено имеет чисто мнимые полюсы

                    

и переходную функцию вида

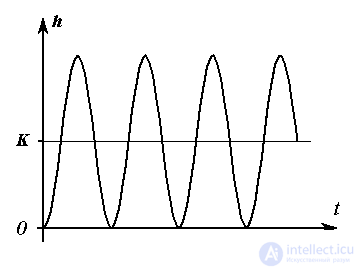
Рис. 2.16. Переходная функция колебательного звена

(2.77)                      ,

где  . Звено не имеет статической характеристики.

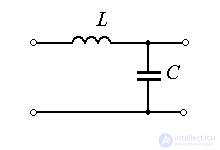
Примеры: маятник в вакууме; идеальный колебательный (LC) контур.

Двойное апериодическое звено. Звено описывается уравнением

(2.78)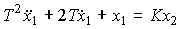                     

или операторным уравнением (2.50), где

(2.79)                      .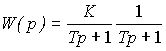

Звено имеет равные вещественные корни характеристического уравнения

                     ,

и переходную функцию

(2.80)                      .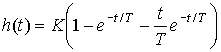

Рис. 2.17. Переходная функция двойного апериодического звена

Статическая характеристика звена

(2.81)                      .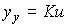

Прочтение данной статьи про элементарные звенья позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое элементарные звенья и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про элементарные звенья