Лекция
Привет, Вы узнаете о том , что такое передаточная функция линейной стационарной системы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое передаточная функция линейной стационарной системы , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Любая система управления представляет собой совокупность нескольких устройств, в которых происходят явления различной физической природы. Одна и та же система может включать в себя, например, механические, электрические, пневматические и гидравлические элементы.
Рассмотрим элементы, в которых процессы преобразования энергии строго ориентированы, то есть энергия и воздействия передаются только в определенном направлении, обладают детектирующим свойством. Это означает, что выходная величина элемента не влияет на свою входную.
Обычно свойством однонаправленности обладают те элементы системы, которые передают информационные воздействия. К таким элементам относятся измерители и преобразователи сигналов.
Первым этапом при исследовании или конструировании системы управления является составление математического описания ее элементов и системы в целом.
Составление математического описания конструктивного элемента системы управления состоит из следующих последовательно выполняемых процедур: принятие определенных допущений, выбор входных и выходных переменных, выбор системы отсчета для каждой переменной, применение физического принципа, отражающего в математической форме закономерности преобразования энергии или вещества.
Автоматическая система 1 вход и 1 выход называется линейной, если ее оператор удовлетворяет принципу суперпозиции, которой выражается следующим равенством:
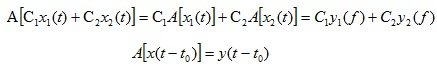(1.1)
Система автоматического управления (далее САУ) называется стационарной, если сдвиг произвольного входного сигнала x(t) на любое время t0 сопровождается таким же сдвигом выходного сигнала y(t), тогда справедливо:
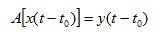(1.2)
Оператором одномерной САУ называется правило, которое определяет единственный выходной сигнал для любой заданной совокупности входных сигналов y(t)=[x1, x2, x3,...] .
Для элемента, имеющего один входной X(t) и один выходной Y(t) сигнал, обыкновенное дифференциальное уравнение записывается в общем случае следующим образом:
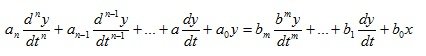(1.3)
a, b – косвенные коэффициенты системы;
x, y – выходной и входной сигналы;
n – порядок выходного сигнала;
m – порядок входного сигнала.
Данное выражение также называют оператором линейной стационарной системы.
Уравнение называют уравнением динамики или уравнением движения элемента. При этом понятие «движение» употребляется в самом обобщенном смысле.
Уравнение может быть линейным и нелинейным. В него, кроме основных переменных, входят постоянные величины, называемые параметрами.
Если в уравнении (1.3) функции времени x(t), y(t) заменить на функции комплексной переменной X(p), Y(p), то оказывается, что дифференциальное уравнение будет равносильно линейному алгебраическому уравнению:
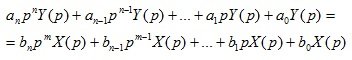(1.4)
Преобразование Лапласа основано на двух следующих формулах:
- прямого преобразования Лапласа
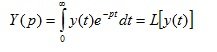(1.5)
- обратного преобразования Лапласа
(1.6)
p - комплексная переменная, t – параметр времени
Операция перехода от исходной функции y(t) к ее изображению Y(p) называется прямым преобразованием Лапласа.Обратное преобразование Лапласа - операция перехода от изображения функции к ее оригиналу.
Передаточной функцией W(p)– называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.
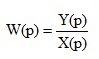(1.7)
Рассматривая линейное дифференциальное уравнение (1.5) и находя изображение для левой и правой частей уравнения, получаем
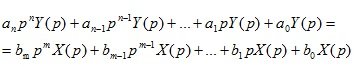(1.8)
Отсюда
(1.9)
Передаточная функция так же, как и дифференциальное уравнение, полностью определяет динамические свойства автоматической системы. Об этом говорит сайт https://intellect.icu . Зная передаточную функцию автоматической системы и изображение входного сигнала, легко найти изображение выходного сигнала:
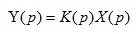(1.10)
Из выражения (1.10), используя обратное преобразование Лапласа, получим
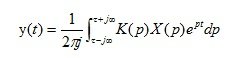(1.11)
Передаточная функция не зависит от вида входного сигнала и полностью определяется структурой и параметрами линейной системы.
Рассмотрим основные свойства передаточной функции. Из выражения (1.9) видно, что в общем случае передаточная функция представляет собой дробно-рациональную функцию комплексного переменного «р». Обозначим
-полином в числителе передаточной функции:
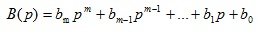(1.12)
-полином в знаменателе передаточной функции
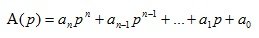(1.13)
Корни уравнения В(р)=0 называются нулями передаточной функции. Корни уравнения А(р)=0 называются полюсами передаточной функции.
Из теории обыкновенных дифференциальных уравнений с постоянными коэффициентами известно, что уравнение
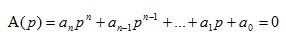(1.14)
представляет собой характеристическое уравнение дифференциального уравнения
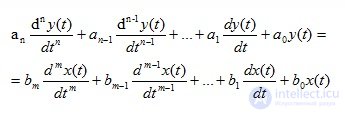(1.15)
Корни характеристического уравнения (1.14) позволяют определить общее решение однородного дифференциального уравнения
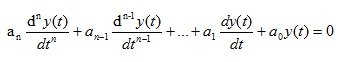(1.16)
Это решение определяет поведение автоматической системы при отсутствии внешних воздействий, т.е. свободное движение системы. С характером свободного движения автоматической системы тесно связаны такие фундаментальные автоматики как устойчивость и качество процесса регулирования. Поэтому в теории автоматического управления большое значение придается исследованию полюсом передаточной функции, а полином (1.13) называют характеристическим полиномом автоматической системы.
Передаточная функция и структура линейной стационарной системы могут быть представлены эквивалентными соединением элементарных динамических звеньев.
Элементарными динамическими звеньями (далее ЭДЗ) называются звенья с простейшими передаточными функциями не выше 2-го порядка, которые нельзя представить произведением более простых ПФ.
ЭДЗ изображается на схеме в виде прямоугольника.
Параметры системы:
k – постоянный коэффициент
T – период времени
p – комплексная переменная
?–коэффициент демпфирования (коэффициент затухания)
Типовые динамические звенья
1.Колебательное звено
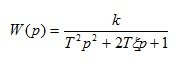(1.17)
2. Консервативное звено
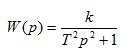(1.18)
3. Апериодическое (инерционное) звено 2 порядка
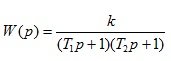(1.19)
4. Апериодическое (инерционное) звено 1 порядка
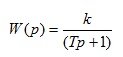(1.20)
5. Форсирующее звено 1 порядка
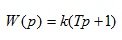(1.21)
6. Форсирующее звено 2 порядка
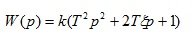(1.22)
7. Усилительное звено (безынерционное, пропорциональное).
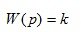(1.23)
8. Идеально-интегрирующее звено
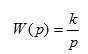(1.24)
9. Идеально-дифференцирующее звено
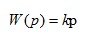(1.25)
Прочтение данной статьи про передаточная функция линейной стационарной системы позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое передаточная функция линейной стационарной системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про передаточная функция линейной стационарной системы
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления