Лекция
Привет, Вы узнаете о том , что такое правила эквивалентных преобразований структурных схем систем автоматического управления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое правила эквивалентных преобразований структурных схем систем автоматического управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Выше были рассмотрены математические модели отдельных динамических звеньев. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ –
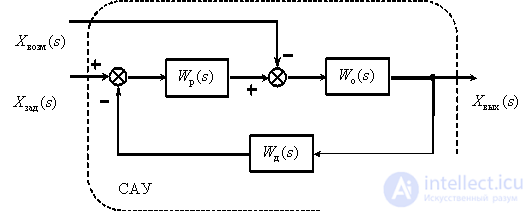
где 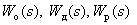 – передаточные функции соответственно объекта, датчика и регулятора,
– передаточные функции соответственно объекта, датчика и регулятора, 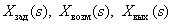 – изображения задающего, возмущающего и выходного сигналов.
– изображения задающего, возмущающего и выходного сигналов.
В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.
Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.
Решением этих задач мы и займемся в дальнейшем.
Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).
Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.
Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:
Последовательное соединение динамических звеньев.
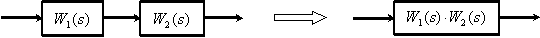
Параллельное соединение динамических звеньев.
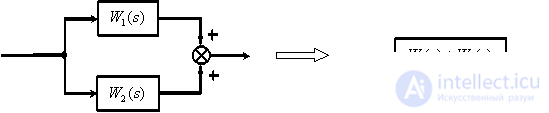
Замкнутый контур с отрицательной обратной связью.

Замкнутый контур с положительной обратной связью.

Перенос точки ветвления через динамическое звено.
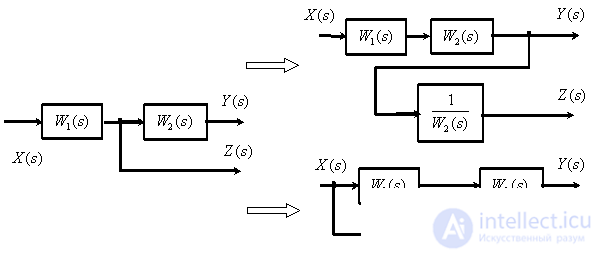
Перенос суммирующего звена через динамическое звено.

Перестановка суммирующих звеньев.
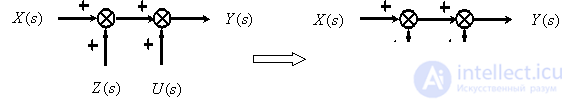
Перенос точки ветвления с выхода на вход суммирующего звена.
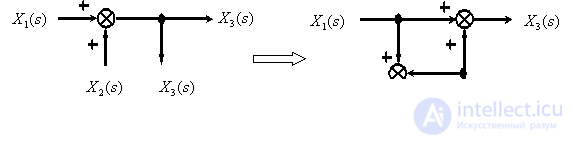
Перенос точки ветвления с входа на выход суммирующего звена.
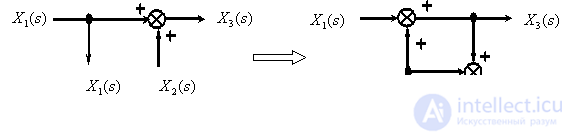
Принцип суперпозиции (наложения)
Применим рассмотренные правила для упрощения структурной схемы

Рис. Об этом говорит сайт https://intellect.icu . 1
Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.
Перенесем суммирующее звено 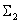 через динамическое звено
через динамическое звено  .
.

Поменяем местами суммирующие звенья  и
и .
.

Преобразуем последовательно включенные динамические звенья 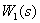 и
и 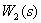 .
.

Преобразуем замкнутый контур с отрицательной обратной связью ( ).
).
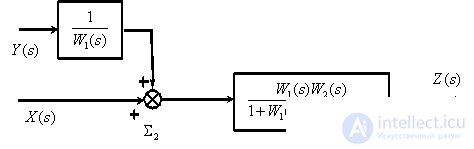
Перенесем суммирующее звено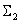 вправо.
вправо.
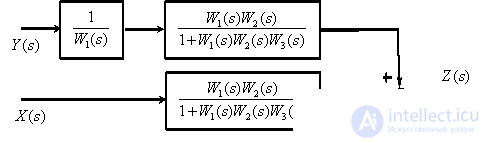
Преобразуем последовательно включенные звенья..
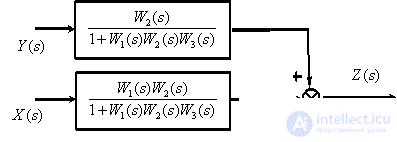
В соответствии с полученной структурной схемой запишем операторное уравнение –
|
|
(1) |
Уравнение показывает, что  является линейной комбинацией изображений входных сигналов, взятых с коэффициентами
является линейной комбинацией изображений входных сигналов, взятых с коэффициентами  и
и 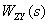 . Выясним смысл этих коэффициентов на примере коэффициента
. Выясним смысл этих коэффициентов на примере коэффициента 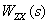 . Для этого положим в (1)
. Для этого положим в (1)  , тогда получим –
, тогда получим –
|
|
(2) |
Таким образом, из (2) следует,  – это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме
– это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме  , равны нулю.
, равны нулю.
Теперь становится ясным смысл и самого операторного уравнения (1), описывающего систему. Он заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.
По сути – это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.
Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.
Рассмотрим использование принципа суперпозиции на примере показанной на рис. 1 структурной схемы.
Полагаем 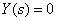 и изобразим соответствующую этому случаю структурную схему.
и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим –
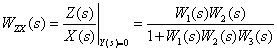 .
.
Полагаем 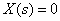 и изобразим соответствующую этому случаю структурную схему.
и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим –
 .
.
Имея 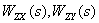 , в соответствии с принципом суперпозиции получим "свернутую" структурную схему САУ.
, в соответствии с принципом суперпозиции получим "свернутую" структурную схему САУ.

Контрольные вопросы и задачи
Какие задачи позволяют решать правила эквивалентных преобразований структурных схем?
Дайте определение принципа суперпозиции применительно к структурным схемам систем автоматического управления.
Как используют принцип суперпозиции на практике?
Определите передаточные функции
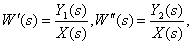
по следующей структурной схеме
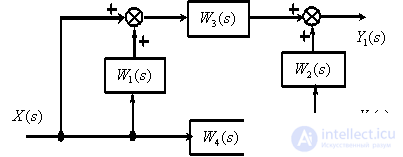
Ответ:
 .
.
Определите передаточную функцию, эквивалентную структурной схеме.

Ответ:
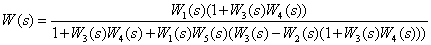 .
.
Определите передаточные функции
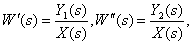
по следующей структурной схеме

Ответ:
 .
.
Определите передаточные функции

по следующей структурной схеме

Ответ:
Прочтение данной статьи про правила эквивалентных преобразований структурных схем систем автоматического управления позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое правила эквивалентных преобразований структурных схем систем автоматического управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про правила эквивалентных преобразований структурных схем систем автоматического управленияОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления