Лекция
Привет, Вы узнаете о том , что такое частотные характеристики динамического звена, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое частотные характеристики динамического звена , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Частотной характеристикой динамического звена называют функцию комплексного аргумента 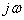 , полученную путем формальной замены
, полученную путем формальной замены 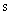 на
на 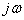 в выражении передаточной функции
в выражении передаточной функции

Получим связь частотной характеристики с известными понятиями. Для этого рассмотрим динамическое звено с передаточной функцией 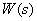 и сигналами
и сигналами 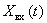 ,
,  . Пусть
. Пусть 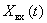 ,
, 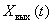 – абсолютно интегрируемые функции и равны нулю при
– абсолютно интегрируемые функции и равны нулю при 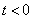 . Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
. Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
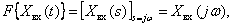
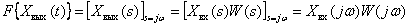 .
.
Получим отношение спектров
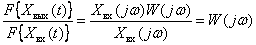 .
.
Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала.
Знание частотной характеристики звена позволяет определить выходной спектр по входному
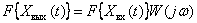 .
.
Рассмотрим динамическое звено –
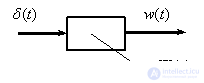
Рис. 1
Получим спектр выходного сигнала – импульсной характеристики
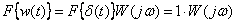 .
.
Тогда имеем
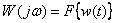 ,
,
то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена.
Частотная функция характеристика как функция комплексного аргумента может быть представлена в следующем виде –
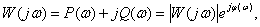
где 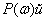 – действительная (вещественная) часть
– действительная (вещественная) часть  ,
,
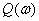 – мнимая часть
– мнимая часть  ,
,
 – модуль (амплитуда)
– модуль (амплитуда) 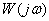 ,
,
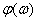 – фаза аргумент
– фаза аргумент 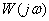 .
.
Амплитуда, фаза, действительная и мнимая части частотной характеристики являются функциями частоты, поэтому частотная характеристика используется и графически представляется в виде амплитудно-фазовой, действительной, мнимой, амплитудной и фазовой частотных характеристик.
В теории автоматического управления рассматривают и используют следующие частотные характеристики динамических звеньев:
Амплитудно-частотная характеристика (АЧХ) –
 .
.
Фазочастотная характеристика (ФЧХ) –
 .
.
Вещественная частотная характеристика (ВЧХ) –
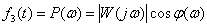 .
.
Мнимая частотная характеристика (МЧХ) –
 .
.
Амплитудно-фазовая частотная характеристика (АФЧХ), которая определяется как годограф (след движения конца) вектора  , построенный на комплексной плоскости при изменении частоты от 0 до
, построенный на комплексной плоскости при изменении частоты от 0 до 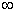 .
.
На рис. Об этом говорит сайт https://intellect.icu . 2 покажем частотные характеристики некоторого динамического звена.

Рис. 2
Для выяснения физического смысла частотной характеристики рассмотрим динамическое звено с передаточной функцией 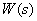 и импульсной характеристикой
и импульсной характеристикой 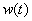 , на вход которого подаем гармонический сигнал
, на вход которого подаем гармонический сигнал 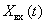 .
.
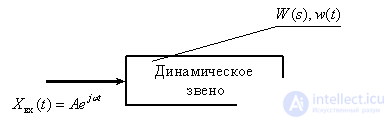
Рис. 3
Вспомним, что решение линейного дифференциального уравнения динамического звена, в рамках классического метода, состоит из двух составляющих – свободной и установившейся.
Установившаяся составляющая в случае гармонической функции времени, стоящей в правой части уравнения, так же является гармонической функцией времени. Поэтом установившийся сигнал на выходе динамического звена можно описать следующим выражением
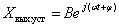 .
.
Сигнал на выходе звена определим с помощью теоремы об умножении изображений

В результате получаем
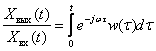 .
.
Для перехода к установившемуся режиму полагаем 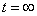 , тогда получаем
, тогда получаем
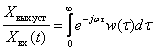 .
.
Но, с другой стороны, имеем по определению прямого преобразования Фурье
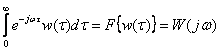 .
.
Поэтому
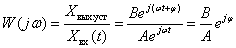 .
.
Отсюда следует простой алгоритм экспериментального определения частотной характеристики линейного динамического звена, объекта или системы управления для конкретной частоты 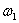 :
:
Подать на вход объекта синусоидальный сигнал частоты 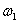 и постоянной амплитуды.
и постоянной амплитуды.
Дождаться затухания свободной составляющей переходного процесса.
Измерить амплитуду выходного сигнала и сдвиг его по фазе относительно входного сигнала.
Отношение амплитуды выходного установившегося сигнала к амплитуде входного сигнала определит модуль частотной характеристики при частоте 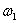 .
.
Сдвиг фазы выходного сигнала относительно входного сигнала определит угол (аргумент) частотной характеристики при частоте 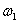 .
.
Применяя данный алгоритм для частот от нуля до бесконечности, можно экспериментальным путем определить частотную характеристику конкретного устройства. Функциональная схема экспериментальной установки для снятия частотных характеристик имеет вид

Рис. 4
При частоте 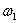 на экране осциллографа получаем после затухания свободной составляющей следующую картину –
на экране осциллографа получаем после затухания свободной составляющей следующую картину –
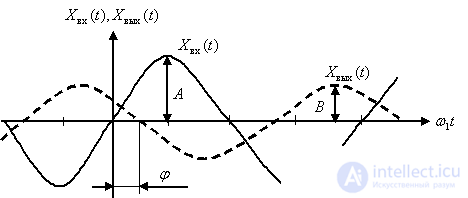
Рис. 5
На основании рис. 5 можно построить на комплексной плоскости точку, принадлежащую частотной характеристике устройства, а совокупность точек при изменении частоты от нуля до величины, когда амплитуда выходного установившегося сигнала станет пренебрежимо мала, будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ). Как видно из рисунка, по этим данным может быть построена любая необходимая частотная характеристика устройства.

Рис. 6
Для экспериментального получения частотных характеристик различных объектов в инженерной практике используют специализированные приборы, а в последнее время широко используют для таких целей персональные компьютеры, оснащенные специализированными платами ввода-вывода и пакетами прикладных программ.
Учитывая все вышеизложенное, становится ясным и физический смысл частотной характеристики.
Она показывает, во сколько раз изменяет динамическое звено (устройство), работающее в установившемся режиме, амплитуду входной синусоиды частоты 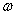 , и на какой угол сдвигает входную синусоиду по фазе.
, и на какой угол сдвигает входную синусоиду по фазе.
Контрольные вопросы и задачи
Как определить частотную характеристику динамического звена, если известна его передаточная функция?
Какие виды частотных характеристик вы знаете?
Как определить амплитуду и аргумент частотной характеристики?
Перечислите основные этапы экспериментального снятия частотной характеристики устройства.
Поясните физический смысл частотной характеристики линейного динамического звена.
Определите выражение частотной характеристики по заданной передаточной функции
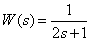 .
.
Ответ:
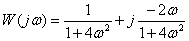 .
.
Определите выражение частотной характеристики по заданной передаточной функции
 .
.
Ответ:
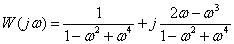 .
.
Определите выражения амплитудной и фазовой частотных характеристик для динамического звена с передаточной функцией –
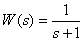 .
.
Ответ:
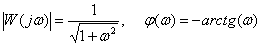 .
.
На вход динамического звена с передаточной функцией
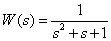 ,
,
поступает гармонический сигнал постоянной амплитуды с частотой
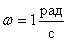 .
.
На какой угол будет смещен выходной сигнал в установившемся режиме?
Ответ:

Прочтение данной статьи про частотные характеристики динамического звена позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое частотные характеристики динамического звена и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про частотные характеристики динамического звенаОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления