3.4 Эквивалентные преобразования моделей ВСВ и канонические представления

Привет, Вы узнаете о том , что такое эквивалентные преобразования моделей всв, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое эквивалентные преобразования моделей всв, канонические представления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Как отмечалось в п. 3.1.1, возможны различные способы выбора переменных состояния динамической системы. Неоднозначность такого выбора определяет неединственность моделей вход-состояние-выход [М4], [М5] (или [М6], [М7]), соответствующих конкретной модели вход-состояние [M1] ([М2] или [М3]), так как выбор иных переменных состояния приводит к получению другой модели ВСВ. С другой стороны первоначальная модель ВСВ может быть специально преобразована, что обычно связывают с изменением базиса (системы координат) пространства состояний . Такого рода преобразование называется эквивалентным, или преобразованием подобия .

3.4.1. Эквивалентное преобразование . Пусть модель вход-выход одноканальной системы (объекта управления) задается операторным уравнением

(3.93)                     a(p)y(t) = b(p)u(t),

где

 .

и  - корни характеристического уравнения (полюсы системы), или уравнением [М3] , где

(3.94)                      ,

а модель ВСВ получена в форме [М6], [М7]. Введем в рассмотрение новый (преобразованный) вектор состояния:

(3.95)                      ,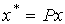

где  - матрица преобразования (подобия), удовлетворяющая условию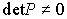 . Тогда существует обратное преобразование

(3.96)                      .

Дифференцируя (3.95) и подставляя (3.96), [М6] находим:

(3.97)                     

и

(3.98)                      .

Полученные выражения перепишем в виде

[М6^*]                      ,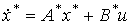

[М7^*]                     ,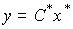

где

(3.99)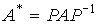                     

(матрица подобная A),

(3.100)                      ,

(3.101)                      .

Подобные матрицы имеют следующие свойства:

а)   

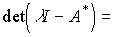
б )   

Модель [М6^* ], [М7^* ] называется эквивалентной (подобной) модели [М6], [М7]. Об этом говорит сайт https://intellect.icu . Справедливо очевидное свойство:

(3.102)                       ,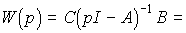

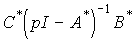т.е. для подобных систем сохраняются связи выходных и входных переменных, а следовательно и модели ВВ [М1], [М2], [М3].

3.4.2. канонические представления моделей ВСВ . Наиболее простые модели вход-состояние-выход, соответствующие исходным уравнениям системы [М6], [М7], называются каноническими представлениями ( формами ).

Диагональной формой называется модель, представленная уравнениями состояния

(3.103)                     

и уравнением выхода

(3.104)                      .

(рис. 3.24). Модель может быть записана в компактной форме [М6*] [M7*], где

                 ,  ,  .

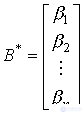К диагональной форме приводятся системы с различными полюсами   . При этом (см. п. 3.1.3) матрицы основной и преобразованной системы связаны соотношением

(3.105)                      ,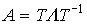

т.е. матрица преобразования находится как

(3.106)                      .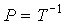

Рис. 3.24. Структурная схема канонической (диагональной) формы

Модель полностью управляемой системы [10] может быть приведена к управляемой (фробениусовой)) канонической форме

(3.107)                     

и

(3.108)                      ,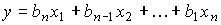

(рис. 3.25). Этой форме соответствуют векторно-матричные уравнения [M6*] [M7*], в которых

                  ,  ,

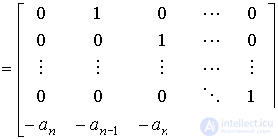                    C^*=[b_n b_n-1 ... b₂ b₁],

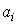 и 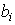 - коэффициенты уравнения (3.107),

                    a^T=[-a_n - a_n-1 ... -a₂ -a₁], 0=[0 0...0 0] ^T,

I - единичная матрица размера ( n-1) 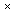 (n- 1). Матрица состояния  называется сопровождающей матриц ей полинома или Фробениусовой матрицей.

Рис. 3.25. Каноническая управляемая форма

 

Матрица преобразования к канонической управляемой форме находится как

(3.109)                     P=U^*U ^-1,

где U и U^* - матрицы управляемости исходной [10] и канонической [10] модели соответственно. Для случая n =3 имеет место:

 .

Модель полностью наблюдаемой системы (см. [10]) может быть приведена к наблюдаемой (фробениусовой)) канонической форме вида :

(3.110)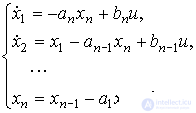                     

и

(3.111)                      ;

(рис. 3.26). Этой канонической форме соответствуют векторно-матричные уравнения [M6*] [M7*], где  - сопровождающая (фробениусова) матрица вида

            , ,  ,

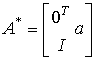
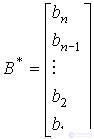Рис. 3.26. Каноническая наблюдаемая форма

Матрица преобразования находится как

(3.112)                     P=(Q^*)^-1Q ,

где Q и Q^* - матрицы наблюдаемости исходной и канонической модели [10]. Для случая n =3 имеет место:

                     .

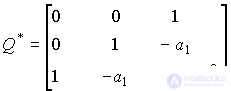Прочтение данной статьи про эквивалентные преобразования моделей всв позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое эквивалентные преобразования моделей всв, канонические представления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про эквивалентные преобразования моделей всв