Логарифмические частотные характеристики систем автоматического управления

Привет, Вы узнаете о том , что такое логарифмические частотные характеристики систем автоматического управления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое логарифмические частотные характеристики систем автоматического управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Апериодическое звено

Передаточная функция –

.

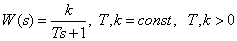Частотная характеристика –

,

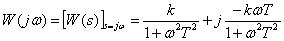АЧХ и ФЧХ

.

Логарифмические характеристики

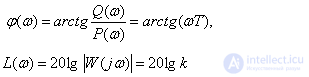
В этом случае, при частоте –

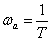
имеем

.

Рассмотри для апериодического звена два характерных диапазона:

(1)

(2)

,

.

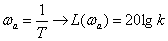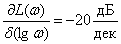Выражения (1) и (2) представляют собой уравнения прямых линий – асимптот, к которым стремиться ЛАЧХ при удалении от точки их сопряжения 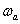. Как мы увидим в дальнейшем, при синтезе и анализе систем бывает удобнее пользоваться не точными, а асимптотическими характеристиками.

Как мы увидели при работе с простейшими типовыми звеньями, частотные характеристики могут быть получены по передаточной функции. В более сложных случаях, при решении задач синтеза и анализа САУ возникает потребность в получении характеристик САУ по известным характеристикам звеньев, входящих в САУ.

Наиболее часто используется случай, когда звенья в САУ включаются последовательно, как это показано на рис. 1.

Рис. 1

В соответствии с правилами эквивалентных преобразований передаточная функция всей САУ будет иметь вид –

.

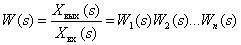Получим частотную характеристику САУ

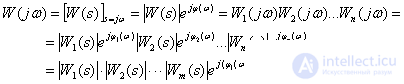
Следовательно,

АЧХ САУ –

(3)

ФЧХ САУ

(4)

Получим по выражениям (3) и (4) логарифмические характеристики САУ:

ЛАЧХ –

(5)

ЛФЧХ –

(6)

Таким образом, логарифмические частотные характеристики САУ могут быть определены, как сумма логарифмических частотных характеристик последовательно включенных составляющих САУ звеньев. Об этом говорит сайт https://intellect.icu . Логарифмические масштабы и использование асимптот позволяет осуществить суммирование графически.

В ТАУ так же используются свойства логарифмических частотных характеристик динамических звеньев, передаточные функции которых взаимообратные –

.

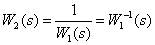Пусть частотные характеристики звена известны:

Частотная характеристика –

,

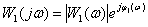ЛАЧХ –

,

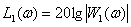ЛФЧХ –

.

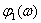Тогда частотные характеристики звена 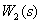 имеют вид:

Частотная характеристика –

,

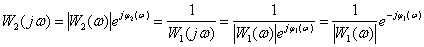ЛАЧХ –

,

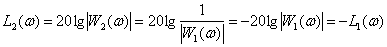ЛФЧХ –

.

Таким образом, ЛАЧХ и ЛФЧХ взаимообратных динамических звеньев расположены симметрично относительно оси частот, подтверждением чему служат полученные ранее ЛАЧХ и ЛФЧХ дифференцирующего и интегрирующего звеньев.

Пример

Для САУ была определена передаточная функция. Следует определить ЛАЧХ САУ.

.

Решение

Представим САУ в виде последовательно включенных динамических звеньев

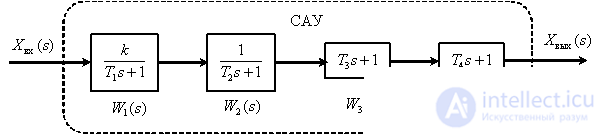
Получим асимптотические ЛАЧХ для каждого апериодического звена

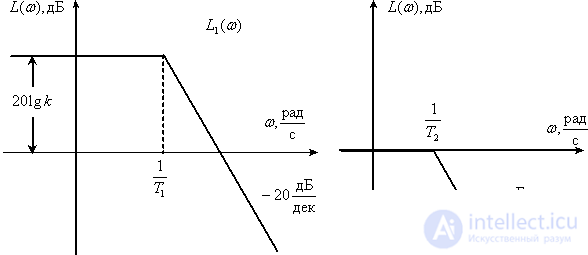
Используя свойства ЛАЧХ взаимообратных звеньев, получим асимптотические ЛПЧХ форсирующих звеньев .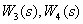

Получим асимптотическую ЛАЧХ САУ выполнив графическое суммирование ЛАЧХ звеньев

.

Задачу существенно упрощает то, что асимптотические графики звеньев имеют участки с целочисленным наклоном.

Получим ЛАЧХ и ЛФЧХ типовых звеньев, используя рассмотренное выше.

 

Реальное дифференцирующее звено

Передаточная функция

.

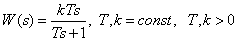Представим звено в следующем виде

Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

 

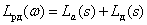Интегрирующее звено с запаздыванием

Передаточная функция

.

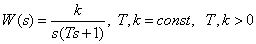Представим звено в следующем виде

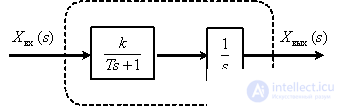
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

 

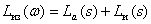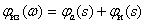Пропорционально-интегральное звено

Передаточная функция

.

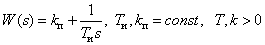Представим звено в следующем виде

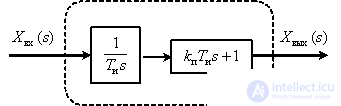
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

 

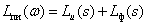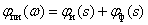Контрольные вопросы и задачи

1. Как можно использовать для получения частотных характеристик системы то, что систему можно представить в виде параллельно включенных типовых динамических звеньев?

2. Как соотносятся ЛАЧХ и ЛФЧХ динамических звеньев, передаточные функции которых являются взаимообратными?

3. На какие последовательно включенные типовые динамические звенья следует разбить реально дифференцирующее звено, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

4. На какие последовательно включенные типовые динамические звенья следует разбить интегрирующее звено с запаздыванием, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

5. На какие последовательно включенные типовые динамические звенья следует разбить пропорционально интегрирующее звено, чтобы получить его асимптотическую ЛАЧХ и ЛФЧХ?

6. Передаточная функция звена –

,

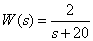При какой частоте ЛФЧХ будет иметь значение .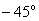

Ответ:

При частоте.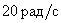

1. Передаточная функция звена –

,

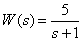Как при частоте 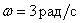 будут отличаться точная и асимптолическая ЛАЧХ этого звена?

Ответ:

Асимптотическая ЛАЧХ будет меньше точной на .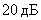

1. Передаточная функция объекта имеет вид –

,

Постройте асимптотическую ЛАЧХ объекта?

Ответ:

Прочтение данной статьи про логарифмические частотные характеристики систем автоматического управления позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое логарифмические частотные характеристики систем автоматического управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про логарифмические частотные характеристики систем автоматического управления

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.