Лекция
Привет, Вы узнаете о том , что такое правила преобразования структурных схем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое правила преобразования структурных схем, отрицательная связь, структурная схема , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Структурную схему любой сложности можно привести к эквивалентной одноконтурной (имеющей одну главную обратную связь) или к эквивалентной разомкнутой структурным схемам.
При наличии большого числа элементов в системе пользуются структурным методом, согласно которому уравнение всей системы получают на основе алгоритмической схемы при помощи нескольких простых правил.
Сущность метода состоит в том, что по известным передаточным функциям отдельных элементов системы, представляющих собой детектирующие звенья однонаправленного действия, используя правила последовательного, параллельного и встречно-параллельного (с обратной связью) соединений звеньев, получают эквивалентную передаточную функцию, или передаточную функцию эквивалентного звена. В результате получают одноконтурную замкнутую цепочку, состоящую из нескольких эквивалентных звеньев.
Причем эта цепочка может иметь несколько входов и несколько выходов. Далее согласно одноконтурной схеме записывают передаточные функции между разомкнутыми входами и выходами системы.
Структурные преобразования схем являются допустимыми, если они сохраняют неизменными все входные и выходные сигналы системы.
Одноконтурные структурно-динамические схемы АС представляют собой замкнутую цепь последовательно соединенных звеньев и определение передаточных функций по таким схемам не представляет больших затруднений. Многоконтурные структурно-динамические схемы характеризуются наличием звеньев, охваченных обратными связями. Поэтому для определения передаточных функций возникает необходимость в преобразовании таких схем к эквивалентным одноконтурным схемам. В общем случае преобразование многоконтурных схем к эквивалентным одноконтурным схемам сводится к замене параллельного соединения и соединения с обратной связью эквивалентными звеньями, а также к перестановке различных элементов схемы (точек съема сигналов, сумматоров, звеньев) как по ходу, так и против хода сигнала.
Элементы структурных схем. Структурной называют схему САУ, показывающую из каких элементов состоит эта САУ и как они соединены между собой. Фактически структурная схема представляет собой графическое изображение математической модели САУ, связывающее входные и выходные переменные элементов САУ через их передаточные функции. Динамические звенья на структурной схеме изображают в виде прямоугольника. Суммирующее звено (рисунок 3.1 а), реализующее уравнение y=x1+x2 и сравнивающее звено (рисунок 3.1 б), реализующее уравнение y=x1-x2, изображают в виде круга, разделенного на секторы, причем сектор, куда подается вычитаемое, зачерняют. Соединение, показанное на рисунке 3.1 в, называют узлом, реализующим функцию размножения сигнала y=x1=x2.
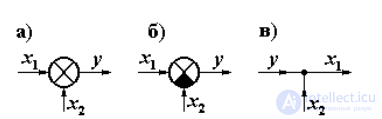
Рисунок 3.1 Обозначения суммирующего (а) , сравнивающего звена (б) и узла (в) в на структурной схеме
Основной принцип перестановки элементов схемы состоит в том, чтобы все входные и выходные величины исходного и преобразованного участка схемы остались неизменными. Выполнение этого принципа при структурных преобразованиях обеспечивает получение одноконтурной схемы, которая эквивалентна (тождественно равноценна) исходной многоконтурной схеме. Основные правила перестановки элементов структурно-динамической схемы, вытекающие из этого принципа, приведены в табл.1. Применение представленных в табл.1 правил позволяет так же решить другую важную практическую задачу. Преобразование многоконтурной структурной схемы может быть произведено таким образом, чтобы упростить вид описывающей ее передаточной функции.
табл.1.
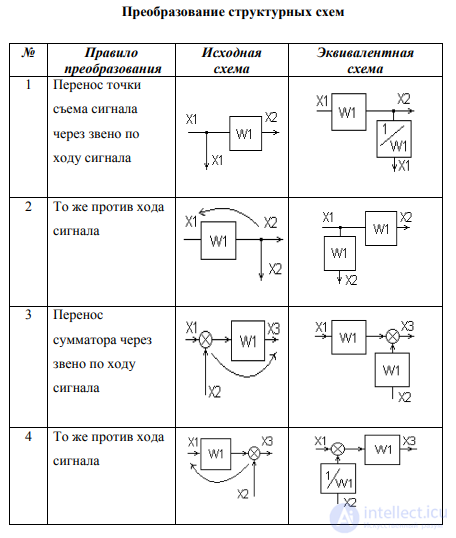
Основные правила преобразования структурных схем
Структурные преобразования схем являются допустимыми, если они сохраняют неизменными все входные и выходные сигналы системы.
Возможность структурных преобразований систем обеспечивается действием принципа суперпозиции и обратимости сигналов:
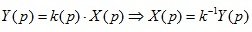 (2.1)
(2.1)
Правило 1: Перестановка однотипных элементов (табл. 2.1)
Таблица 2.1 Перестановка узла (сумматора или звеньев)
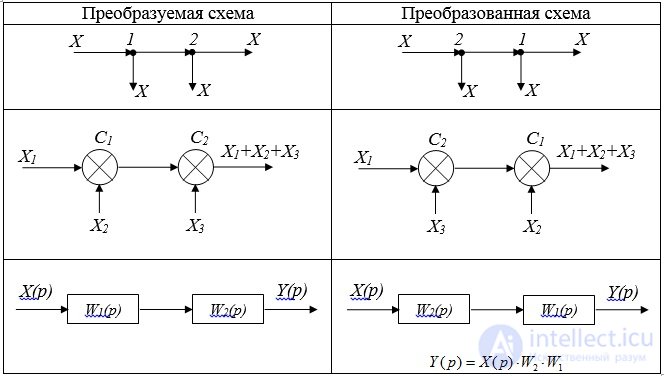
Соседние однотипные элементы можно переставлять местами, при этом ничего не изменяя в самой схеме.
Правило 2: Перенос узла с выхода на вход сумматора (через сумматор против хода сигнала). Такой перенос сопровождается дублированием элемента (сумматора или звена) (Рис. 2.1).
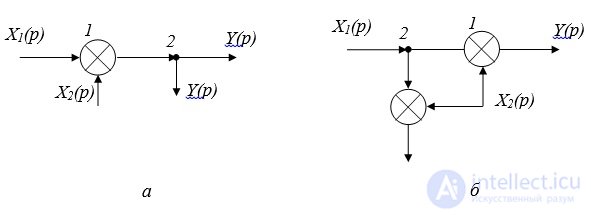
Рис. 2.1. Перенос узла:а - преобразуемая схема; б – преобразованная схема
Правило 3: Перенос узла через звено против хода сигнала (рис. 2.2).
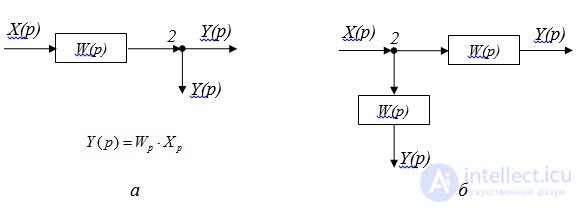
Рис. 2.2. Перенос узла через звено:а - преобразуемая схема; б – преобразованная схема
Правило 4: Перенос узла и звена через сумматор. При таком переносе необходимо в ответвлении узла установить вычитающее устройство (рис. 2.3).
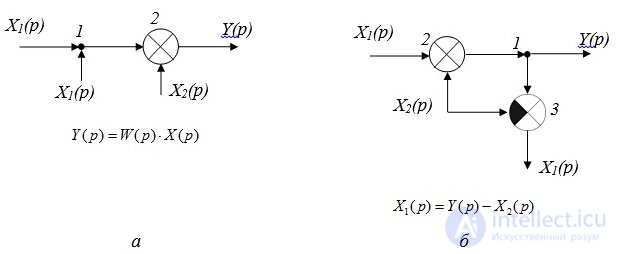
Рис. 2.3. Перенос узла через сумматор по направлению хода сигнала: а - преобразуемая схема; б – преобразованная схема
Правило 5: Перенос звена через сумматор по направлению хода сигнала (рис. 2.4).
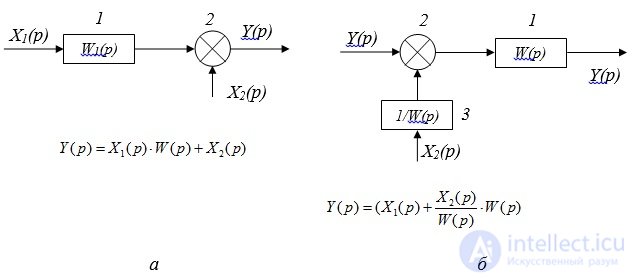
Рис. 2.4. Перенос звена через сумматор: а - преобразуемая схема; б – преобразованная схема
В этом случае в переносимую ветвь добавляется динамическое звено:
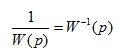
Правило 6: Перенос узла через звено по направлению хода сигнала. При таком переносе в ответвлении узла необходимо установить дополнительное звено с обратной передаточной функцией (рис. 2.5)
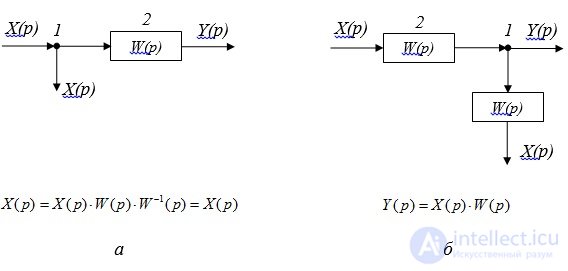
Рис. 2.5. Перенос узла через звено: а - преобразуемая схема; б – преобразованная схема
Правило 7: Перенос звена через сумматор против хода сигнала. В этом случае в переносимую ветвь необходимо добавить звено с той самой передаточной функцией (рис. 2.6).
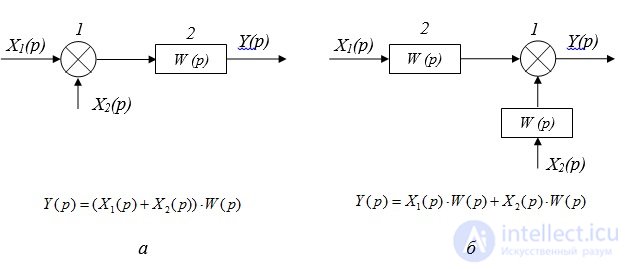
Рис. 2.6. Перенос звена через сумматор: а - преобразуемая схема; б – преобразованная схема
Пример
Упростить структурную схему АС (рис.7) путем ее преобразования.
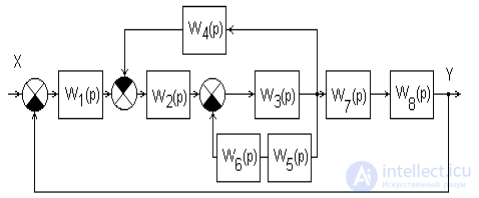
Рис. 7. Исходная многоконтурная схема
Путем поэтапных преобразований получается одноконтурная структурная схема (рис.8) с передаточной функцией
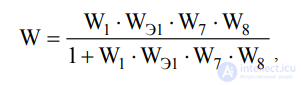
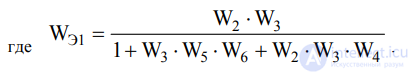
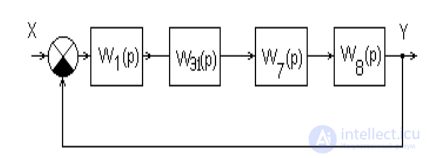

Рис.8. Преобразованная схема
Структурная схема замкнутой двухконтурной системы с обратными отрицательными связями (без перекрестных связей)
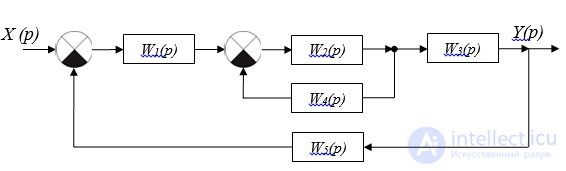
Рис. 2.7. Структурная схема
Формулы для встречно-параллельного соединения можно обобщить для произвольного числа вложенных друг в друга контуров без перекрестных обратных связей.
Для структурной схемы, представленной на рис. 2.7, передаточная функция системы равна:
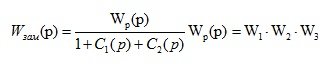 (2.2)
(2.2)
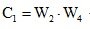 – передаточная функция внутреннего контура системы;
– передаточная функция внутреннего контура системы;
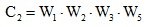 – передаточная функция внешнего контура.
– передаточная функция внешнего контура.
Передаточная функция замкнутой многоконтурной системы без перекрестных обратных связей равна отношению передаточной функции разомкнутой системы к алгебраической сумме единицы и передаточных функций элементов вложенных контуров.
Пример преобразования структурной схемы системы с перекрестной обратной связью (опущен оператор.S) показан на рис. 1.22:
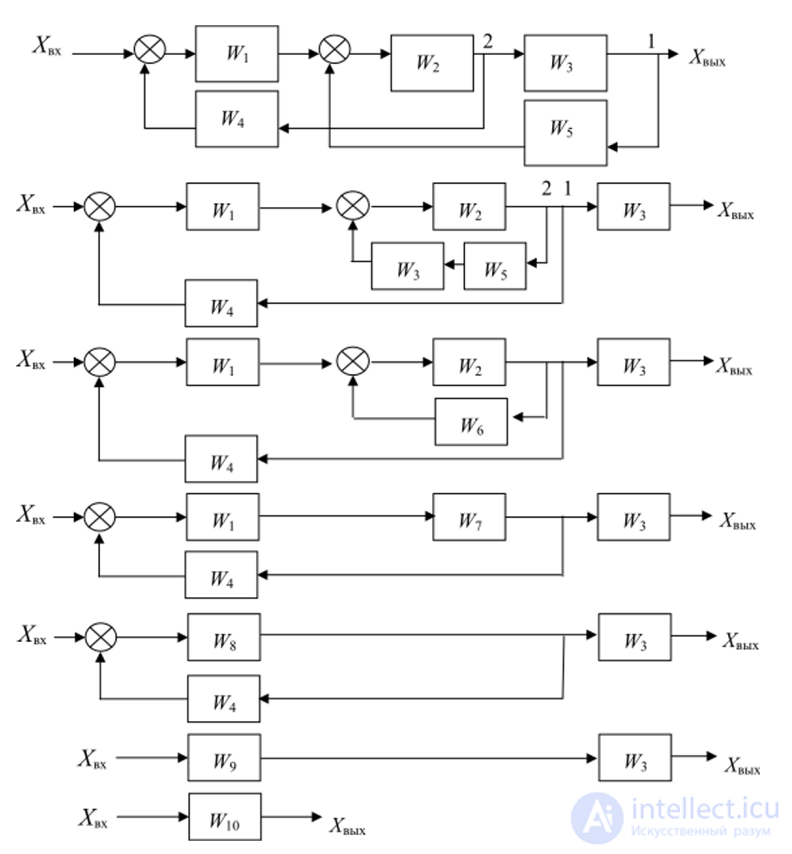
Рис. 1.22. Пример преобразования структурной схемы
Пример 1. Упростив схему, представленную на рис. 2.8, определить какому элементарному динамическому звену соответствует передаточная функция системы.
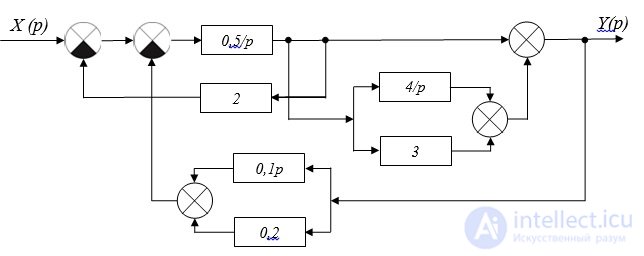
Рис. 2.8. Структурная схема
Решение:
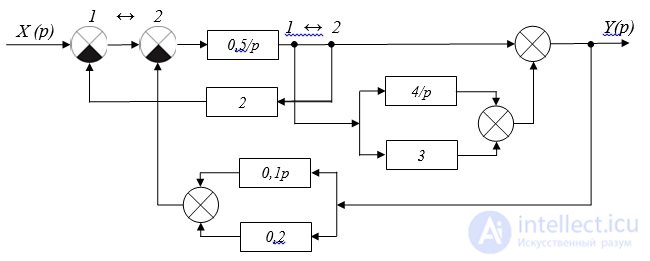
Рис. 2.9. Структурная схема
Получаем структурную схему, представленную на рис. 2.10:
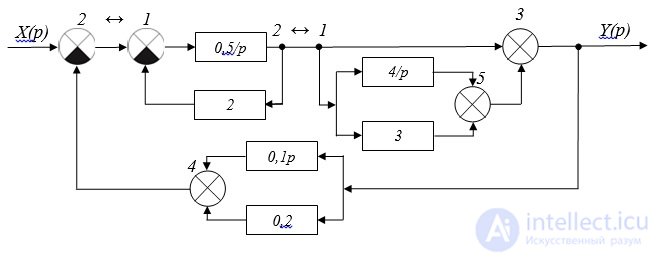
Рис. 2.10. Структурная схема
3. Сложив два сигнала, идущих в сумматор 4, и два сигнала, идущих в сумматор 5 (рис. 2.10), получаем следующую структурную схему (рис. 2.11):
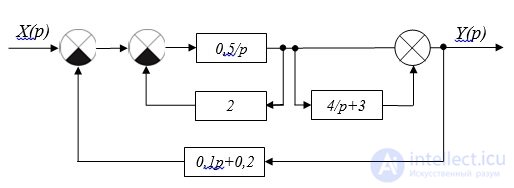
Рис. 2.11. Структурная схема
Параллельное соединение звеньев с передаточными функциями w(p)=4/p и w(p)=3 дает нам звено с передаточной функцией w(p)=4/p+3.
Параллельное соединение звеньев с передаточными функциями w(p)=0,1p и w(p)=0,2 дает нам звено с передаточной функцией w(p)=0,1p+0,2.
4. Параллельное соединение звеньев в сумматор 3 будет равно w(p)=4+4p (рис.2.12.)
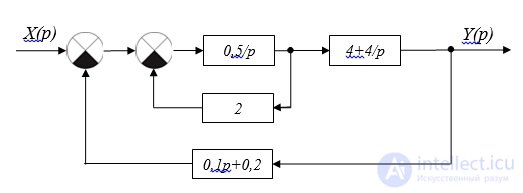
Рис. 2.12. Структурная схема
Передаточную функцию двух звеньев, соединенных встречно-параллельно с отрицательной обратной связью, используя формулу (1.19), можно представить в виде следующего выражения: 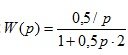 .
.
Запишем передаточную функцию всей системы, представленной на рис.2.12
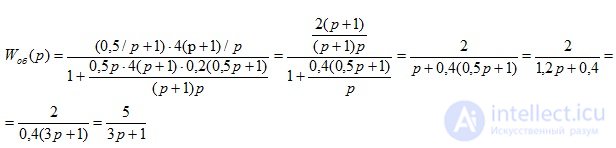
Данная передаточная функция соответствует апериодическому звену 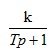 c параметрами k=5, Т=3с.
c параметрами k=5, Т=3с.
Прочтение данной статьи про правила преобразования структурных схем позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое правила преобразования структурных схем, отрицательная связь, структурная схема и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления