Преобразование структурных схем. Граф системы управления.Соответствие структурных схем графам

Привет, Вы узнаете о том , что такое преобразование структурных схем граф системы управления соответствие структурных схем графам, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое преобразование структурных схем граф системы управления соответствие структурных схем графам , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Правила структурных преобразований

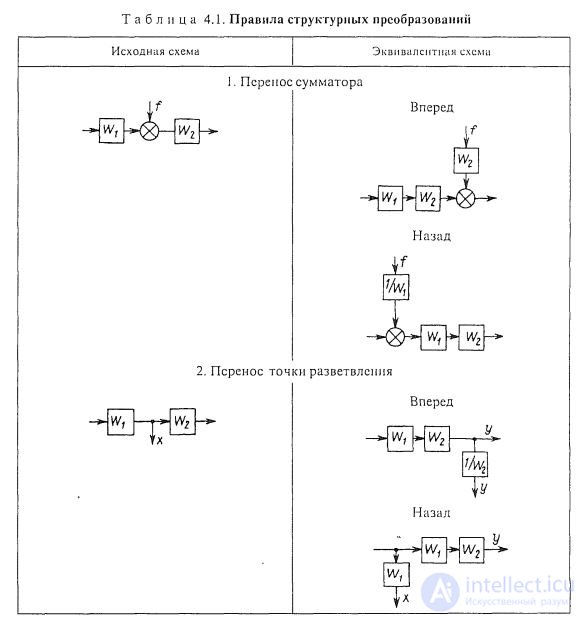
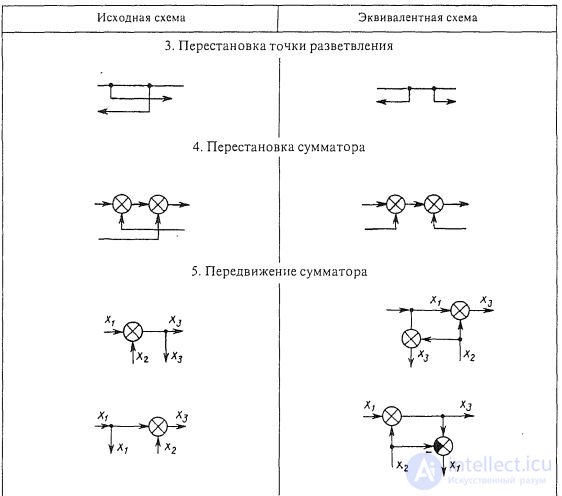
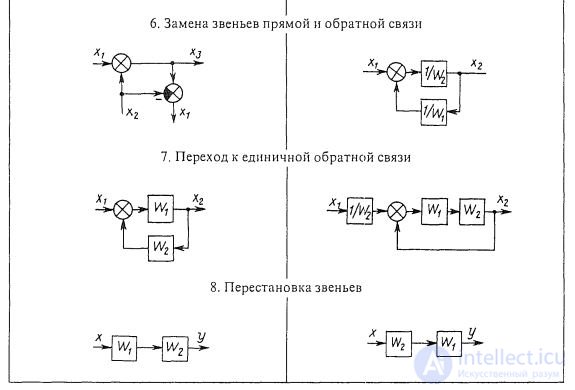
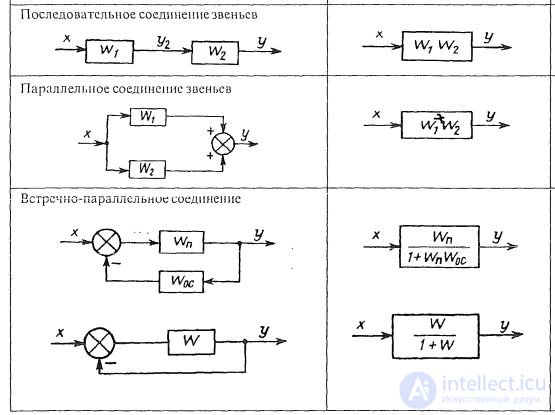
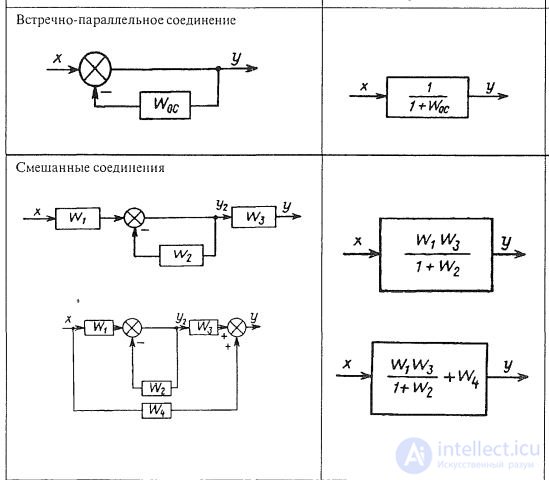
Последовательное соединение звеньев. При последовательном соединении звеньев (рис. 1.8, а) выходная величина предыдущего звена является входной величиной последующего звена. Передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:

W_c(p)=W₁(p) * W₂(p) * W₃(p)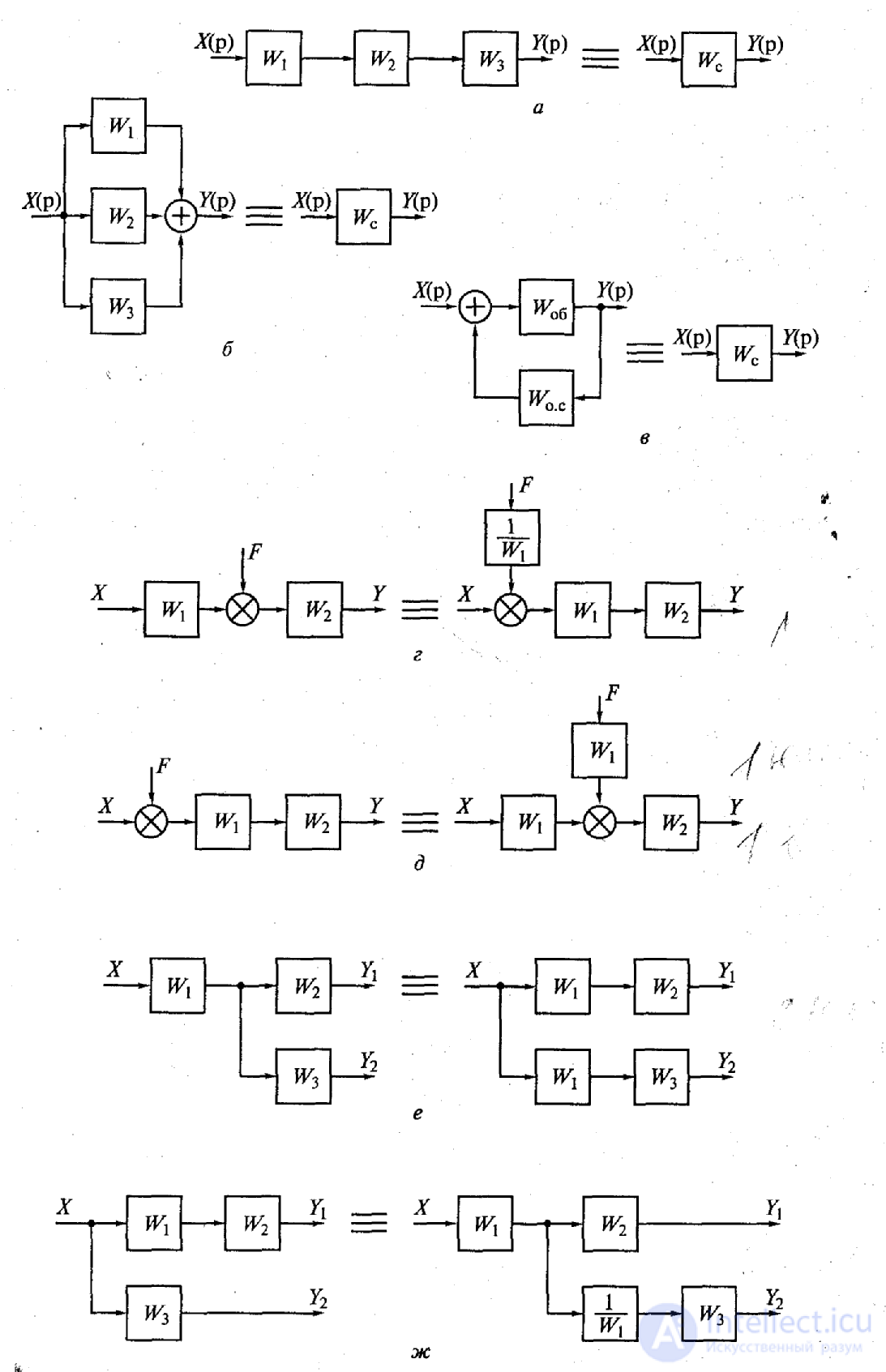



Рис. 1.8. Типы преобразований структурных схем:

а — преобразование передаточных функций последовательного включения трех звеньев в передаточную функцию одного эквивалентного звена; б — преобразование передаточных функций параллельного включения трех звеньев в передаточную функцию одного эквивалентного звена; в — преобразование передаточных функций встречно-параллельного включения двух звеньев в передаточную функцию одного звена; г — перемещение внешнего воздействия из середины схемы на вход; д — перемещение внешнего воздействия со входа в середину схемы; е — перемещение выходного сигнала из середины схемы на вход; ж — перемещение выходного сигнала со входа в середину схемы
Параллельное соединение звеньев. Входная величина системы, состоящей из параллельно соединенных звеньев (рис. 1.8. б), одновременно подается на входы всех звеньев, а ее выходная величина равна сумме выходных величин отдельных звеньев. Передаточная функция системы, состоящей из параллельно соединенных звеньев, равна сумме передаточных функций этих звеньев:

W_c(p)=W₁(p) +W₂(p)+ W₃(p)
Встречно-параллельное соединение звеньев. При встречно-па-раллельном соединении звеньев на вход соединения одновременно с входной величиной системы подается ее выходная величина, прошедшая через звено обратной связи с передаточной функцией W_oc(р) (рис. 1.8, в). Передаточная функция системы определяется выражением:

W_c(p)= 

В знаменателе знак «+» относится к отрицательной обратной связи, знак «-» — к положительной обратной связи. В промышленных системах в основном применяется отрицательная обратная связь.

Схема цепи с отрицательной обратной связью в случае параллелъно-встречного соединения звеньев приведена на рис. 5.6, а. На рис. 5.6, б дана схема соединения двух звеньев с положительной ОС.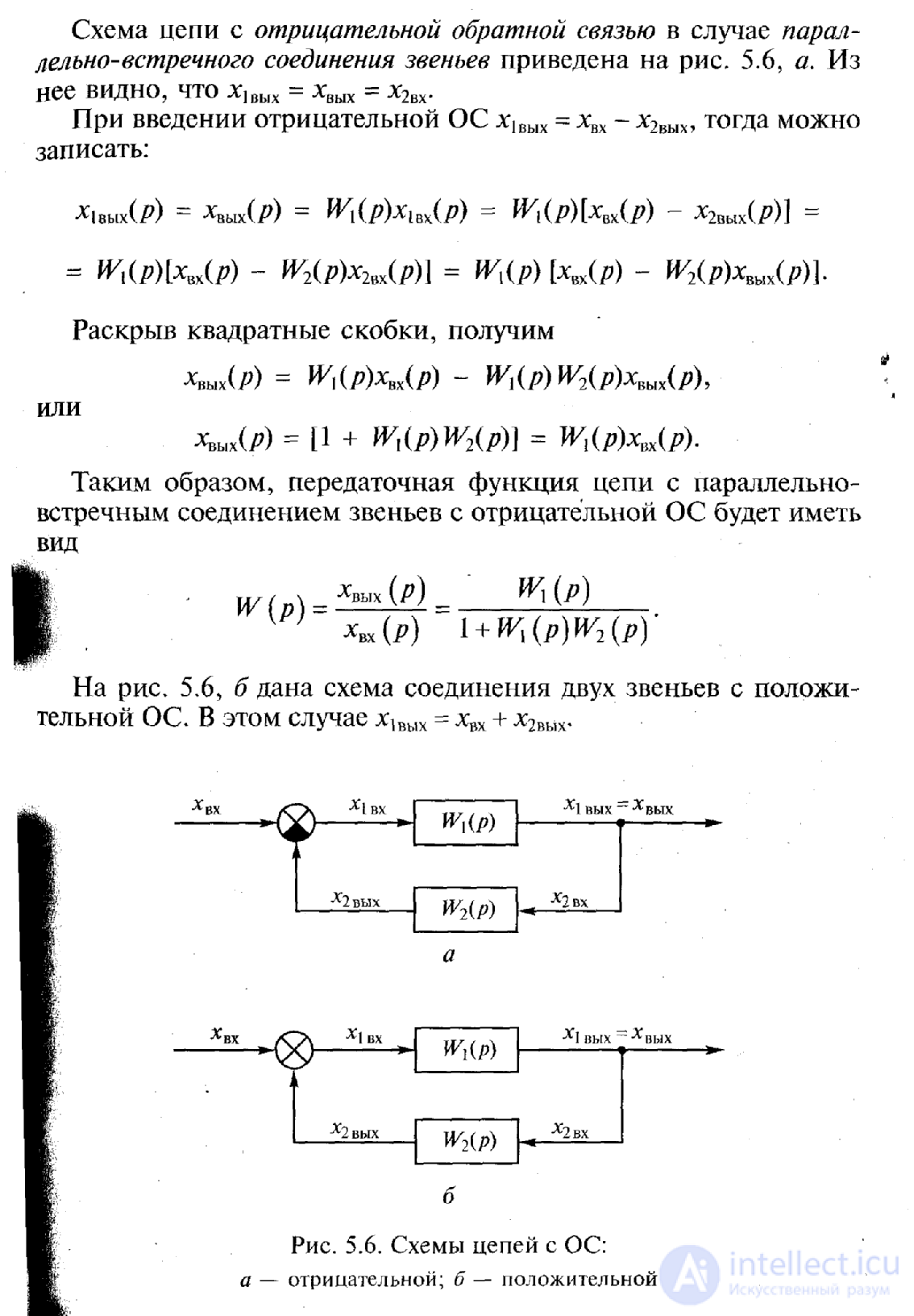 



Таким образом, разбивка дифференциального уравнения, оп-ределяющего процесс автоматического управления в системе, на дифференциальные уравнения элементарных звеньев в общем случае может быть выполнена различными способами. Следовательно, один и тот же процесс управления может быть осуществлен с помощью систем, расчлененных на различное число элементарных звеньев с различными структурными связями между ними. Имея в качестве исходной какую-либо одну из таких систем и определив передаточные функции всех ее элементарных звеньев, можно в дальнейшем упростить структурную схему системы путем ее эквивалентных преобразований. Во всех различных струк-турных схемах, полученных в результате эквивалентных преобразований первоначальной схемы, передаточная функция системы в целом не изменяется и не зависит от того, на сколько и на какие элементарные звенья разделена система и какие структурные связи имеются между ее звеньями.

К уже приведенным преобразованиям структурных схем можно добавить следующие преобразования. Внешнее воздействие F, приложенное к выходу звена с передаточной функцией W₁ (рис. 1.8, г), можно перенести на его вход, поместив между воздействием и входом звена дополнительное звено с передаточной функцией 1/W₁. Внешнее воздействие F, приложенное ко входу звена с передаточной функцией W₁, можно перевести на его выход (рис. 1.8, д), поместив между воздействием и выходом звена дополнительное звено с той же передаточной функцией W₁. Точку присоединения любой структурной связи к выходу звена, имеющего передаточную функцию W₁, можно перенести на его вход, включив в эту связь дополнительное звено с той же передаточной функцией W₁(рис. Об этом говорит сайт https://intellect.icu . 1.8, е). Точку присоединения любой структурной связи ко входу звена с передаточной функцией W₁ (рис. 1.8, ж) можно перевести на его выход, включив в эту связь дополнительное звено с передаточной функцией 1/W₁.

С помощью перечисленных правил структурные схемы с пере-крестными связями можно преобразовать в структурные схемы без перекрестных связей, заменить многоконтурные автоматические системы управления одноконтурными, а также выделить линейную часть в нелинейных автоматических системах управления.

Эти правила лучше всего пояснить на примерах. На рис. 1.9, а показана исходная структурная схема системы, имеющая промежуточную связь. Эту систему можно преобразовать к виду, показанному на рис. 1.9, б, что позволяет использовать полученные ранее соотношения. Преобразованная структурная схема имеет две обратные связи, одна из которых, включающая звенья с передаточными функциями W₃ и W ₅, охватывает звено с передаточной функцией W ₂, а вторая, состоящая из звеньев с передаточными функциями W₃ и W₄ образует главную обратную связь. Следовательно, звено с передаточной функцией W₃вошло в структурную схему дважды. Применяя далее правила вычисления эквивалентных передаточных функций, приходим к простой структурной схеме одноконтурной системы автоматического регулирования (рис. 1.9, в), в прямой цепи которой находится звено с передаточной функцией

W_c=W₁W₂/(1-W₂W₃W₅), (1-9) 

а в цепи обратной связи

W_oc=W₃W_4. (1-10)

Следует заметить, что при достаточном опыте можно установить наличие таких обратных связей без построения структурной схемы, показанной на рис. 1.9, б.

Преобразование структурных схем систем автоматического ре-гулирования, имеющих перекрестные обратные связи, приводит, как правило, к введению в преобразованную структурную схему звеньев с обратными передаточными функциями. Так, структурную схему системы с такими обратными связями (рис. 1.9, г) можно преобразовать к виду, показанному на рис. 1.9, д. Из этого рисунка видно, что главная обратная связь этой системы имеет звено с передаточной функцией 1/W₁. После такого преобразования систему регулирования можно свести к одноконтурной (см. рис. 1.9, в). Передаточная функция звена в прямой цепи определяется как

W₀=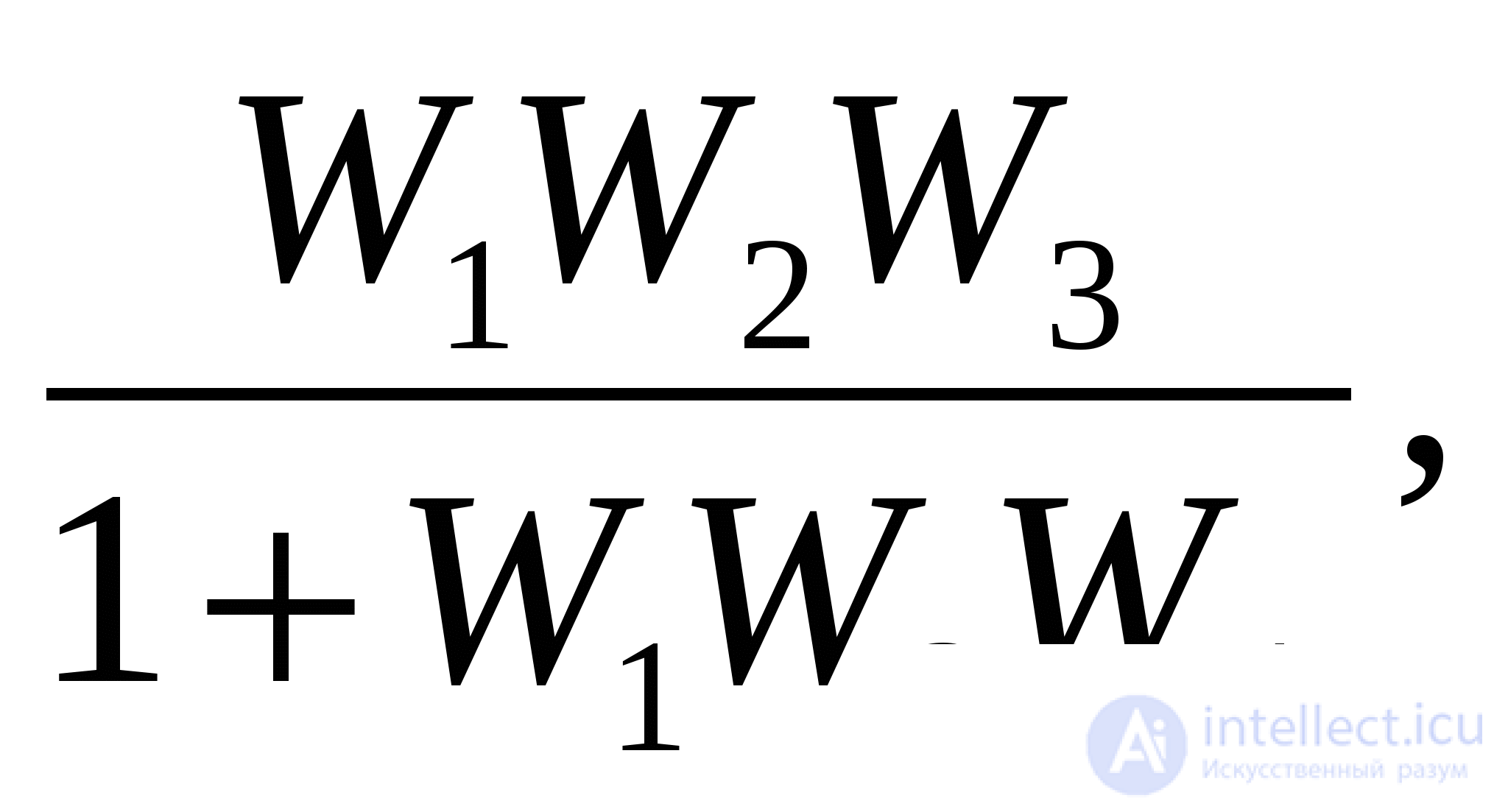

а в цепи обратной связи

W_oc=W₅/W₁.

Применение правил преобразования структурных схем систем автоматического регулирования и определения эквивалентных передаточных функций значительно упрощает анализ таких систем. Однако при экспериментальных исследованиях динамических систем часто возникает обратная задача — отыскание передаточной функции звена, когда известны передаточные функции системы в целом и остальных входящих в нее звеньев. Такая задача решается с помощью рассмотренных ранее правил.



Рисунок 1.9. Преобразования структурной схемы

При параллельном встречном включении может иметь место частный случай Z(p)=1, передаточная функция системы для выходной величины:

Х_вых(р)/Х_вх(р)=W(p)/1+W(p),

Для ошибки: Х(р)/Х_вх(р)=1/1+W(p).

Если W(p)=A(p)/B(p), то

для выходной величины Х_вых(р)/Х_вх(р)=A(p)/A(p)+B(p),

Для ошибки: Х(р)/Х_вх(р)=В(р)/А(р)+B(p).

Сложные соединения звеньев. На рис. 1.10 изображена схема слож-ного соединения звеньев в САУ, на которой нетрудно увидеть типовые соединения. Первое и второе звенья здесь объединены в блок I с параллельно-согласованным соединением, пятое и шестое — в блок III с последовательным соединением. В блок II выделено четвертое звено, охваченное собственной положительной ОС. Условно можно принять, что в эту ОС включено пропорциональное звено с коэффициентом усиления, равным единице. Запишем передаточные функции выделенных блоков:



В свою очередь, блок I, третье звено и блок II соединены пос-ледовательно, а блок III включен в цепь отрицательной ОС. Используя приведенные ранее формулы, запишем передаточную функцию всей САУ:



Рисунок 1.10. Схема сложного соединения элементов САУ

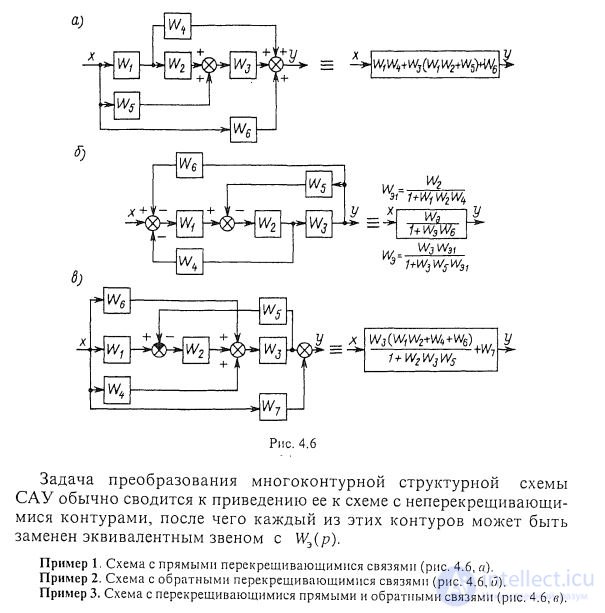
Задача преобразования многоконтурной структурной схемы САУ обычно сводится к приведению ее к схеме с неперекрещивающимися контурами, после чего каждый из этих контуров может быть заменен эквивалентным звеном с Wэ (р).

Передаточные функции сложных САУ можно определить по структурной схеме и без приведения ее к одноконтурной путем применения диаграмм прохождения сигналов (из теории графов). Графы прохождения сигналов подобны структурным схемам и также используются для наглядного изображения математических зависимостей в САУ (см. рис. 4.1). Направленный сигнальный (ориентированный) граф (указано направление сигнала) — более компактная форма записи структурных схем. Правила преобразования графов подобны правилам преобразования структурных схем (см. таблицу 1).

Граф представляет собой совокупность вершин (узлов), начала, конца и ребер. Ребро (ветвь, дуга) тождественно равно оператору W(р). Вершины графа — переменные (сигналы): у, и, х и т. д. В общем случае ребра — коэффициенты а, b, с, Ti, ki и т. д. в уравнениях САУ; дуга направленна и характеризуется символом k(W) (весом дуги).

Структурную схему САУ рассматривают как один из видов графа прохождения сигналов. Направленный (сигнальный) граф САУ строится по уравнениям, записанным, как и структурная схема САУ, в принятой условно-разрешенной форме.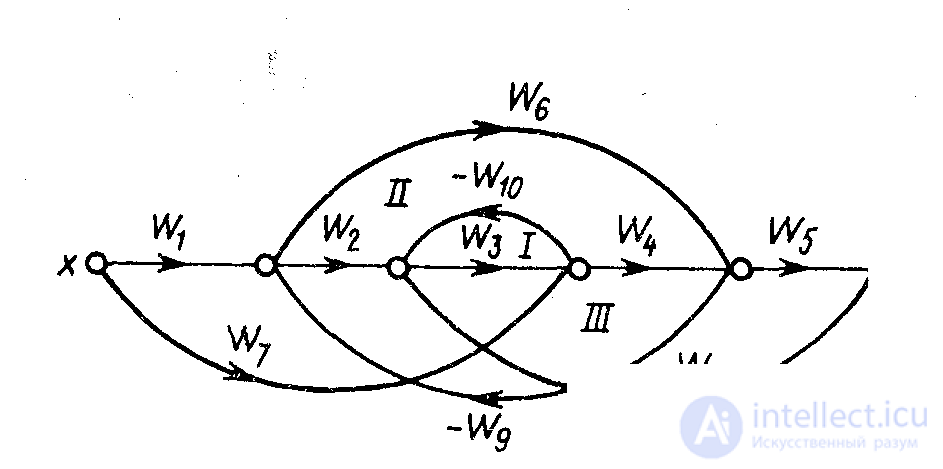



Таблица 1. Алгебра W(p). Соответствие структурных схем графам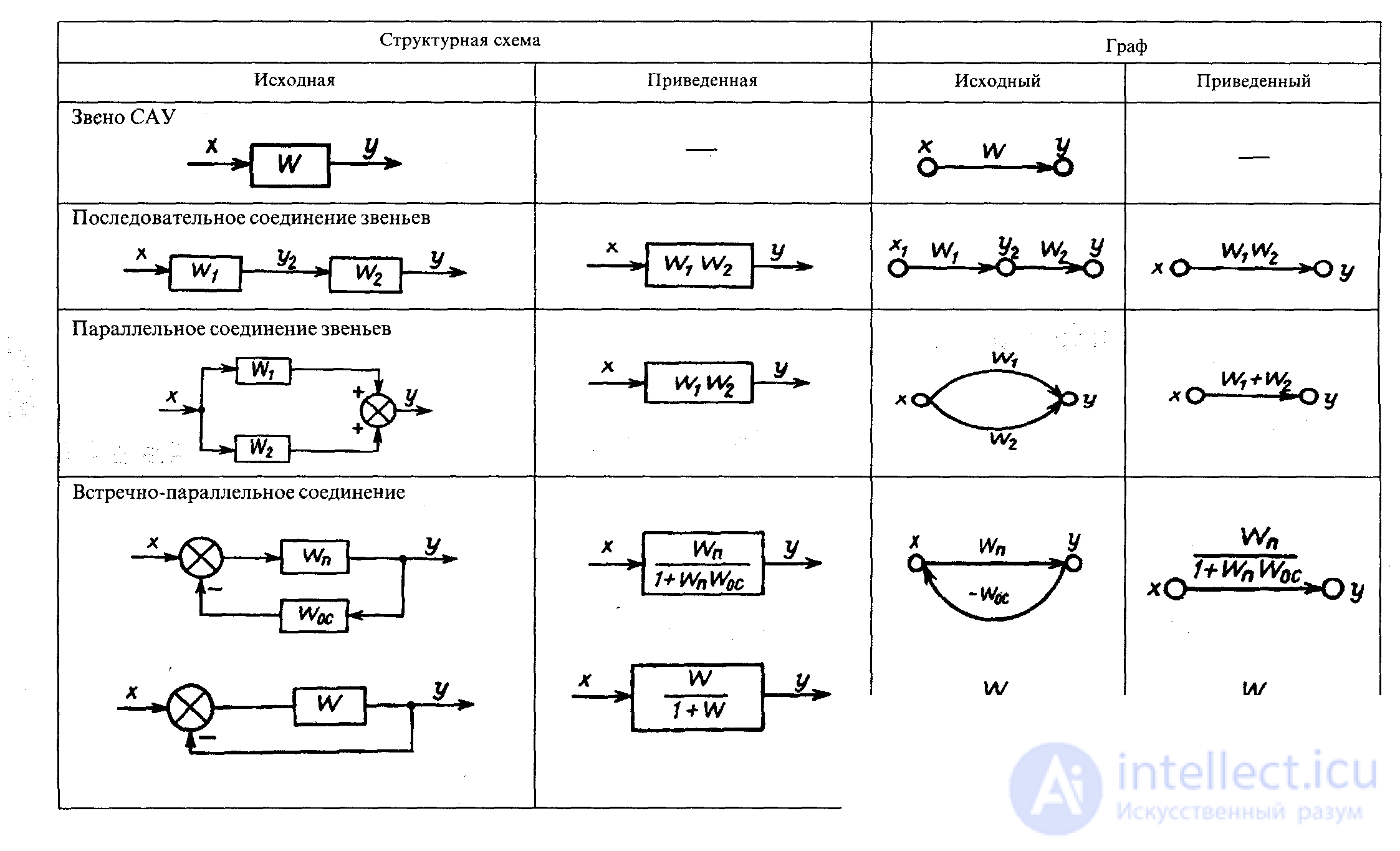

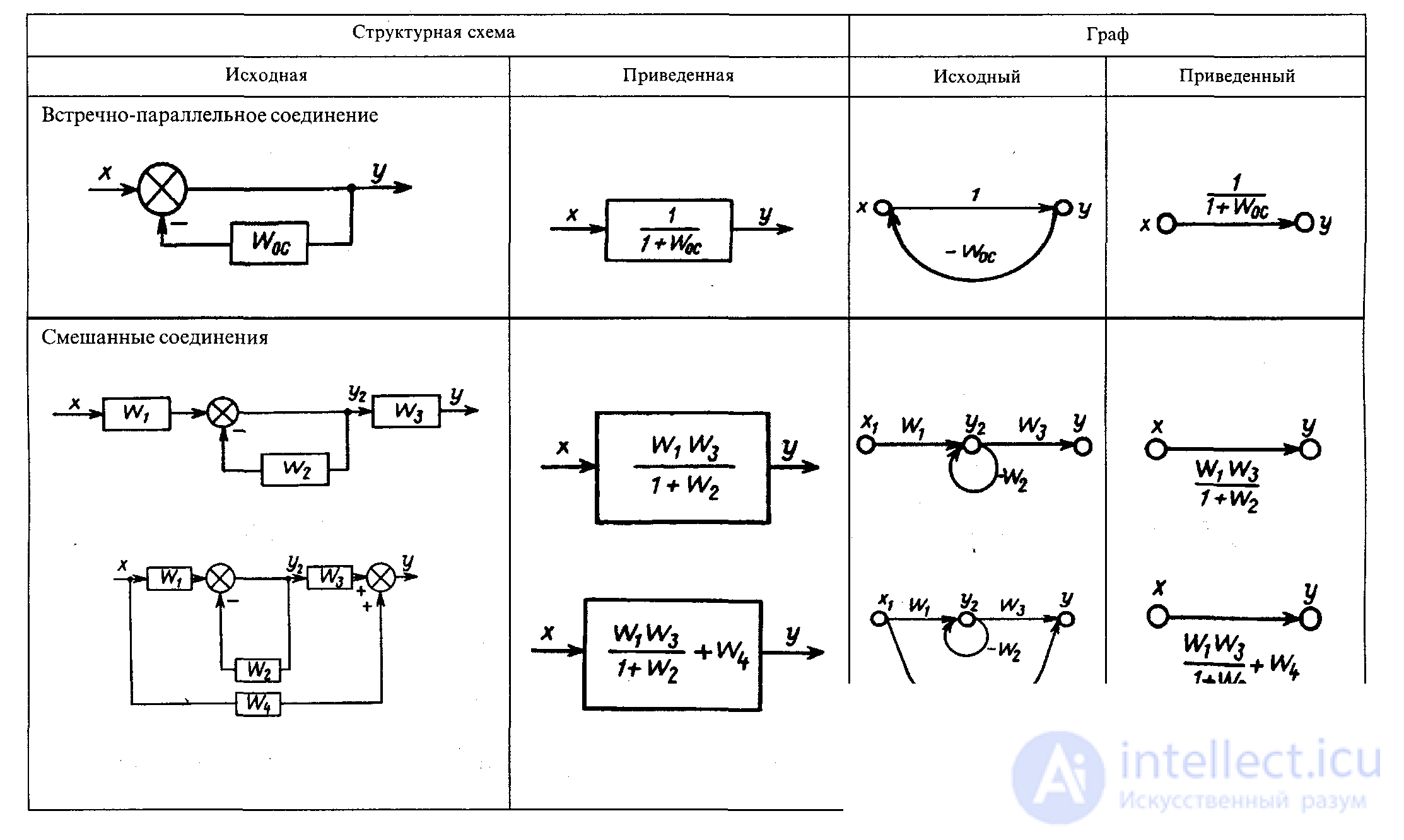
Пример математическая модель системы в виде структурной схемы соотвествующая заданному графу

Задание 1. Преобразовать исходную структурную схему, определив передаточную функцию системы при условии .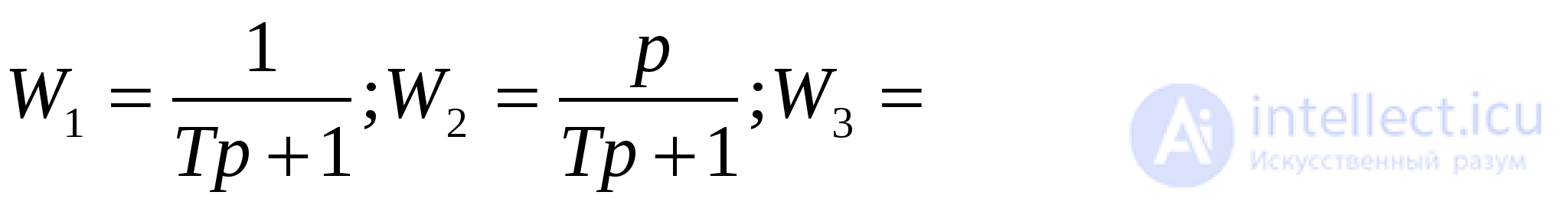

 

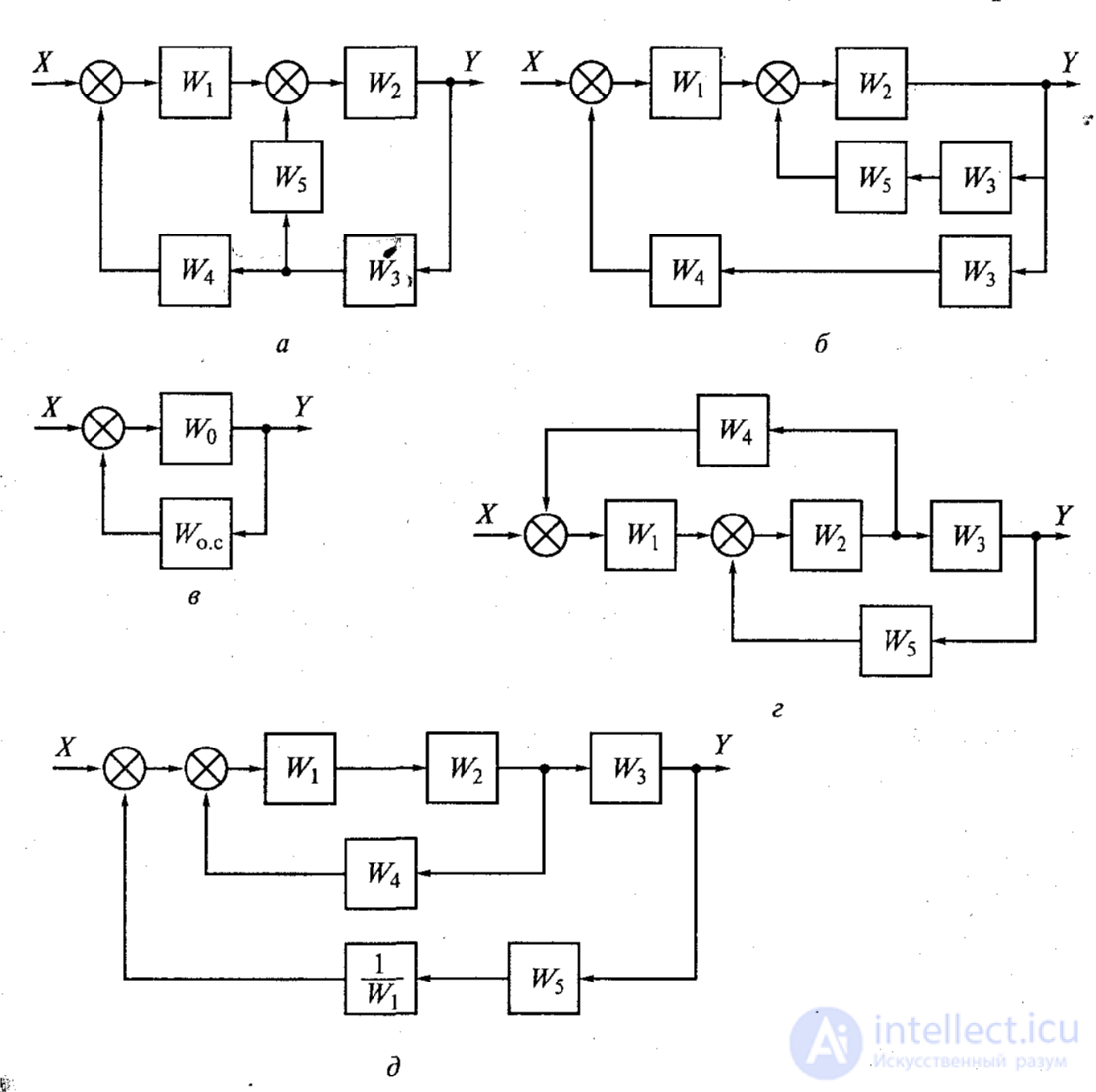
Рис.1а



Рис.1.б

Задание 2. Преобразовать структурные схемы и определить передаточную функцию САУ.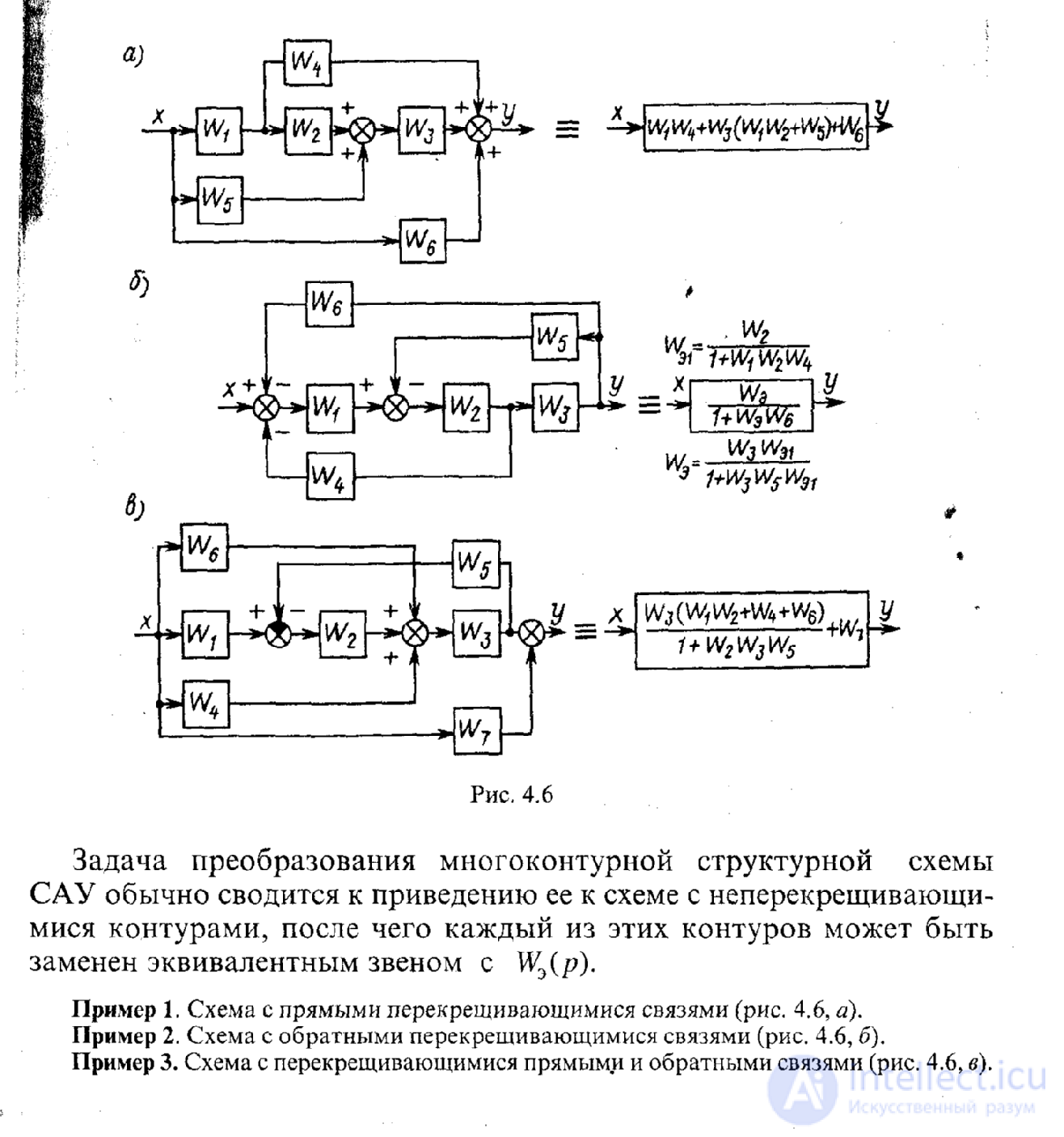







Рисунок 3 

Пример 1 Схема с прямыми перекрещивающимися связями (рис. 3,а).

Пример 2 Схема с обратными перекрещивающимися связями (рис. 3,б).

Пример 3 Схема с перекрещивающимися прямыми и обратными связями (рис. 3,в).

Задание 3. Сверните изображенную на рис. 4 структурную схему САУ и определите ОФП замкнутой системы по основному каналу и ОФП ошибки, если W₁(p)= W₂(p)= W₃(p)=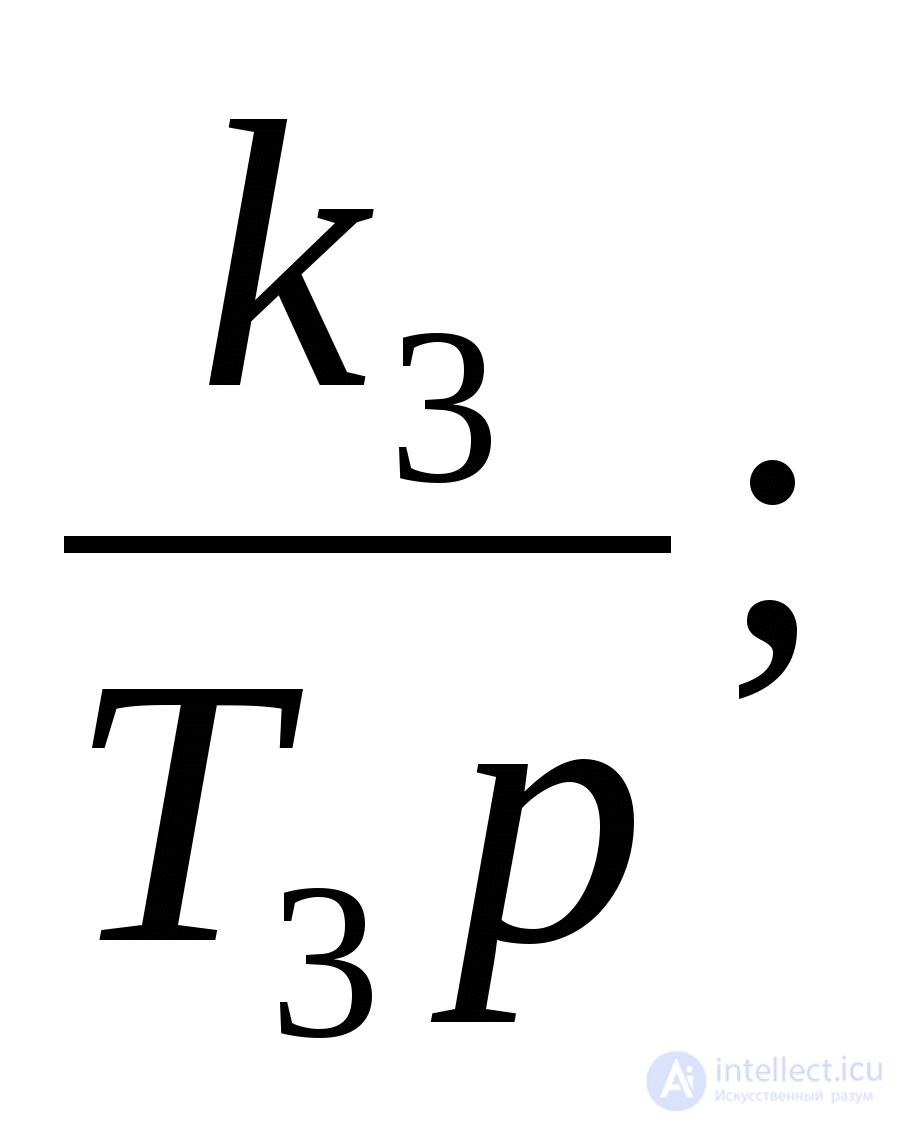 W₄(p)=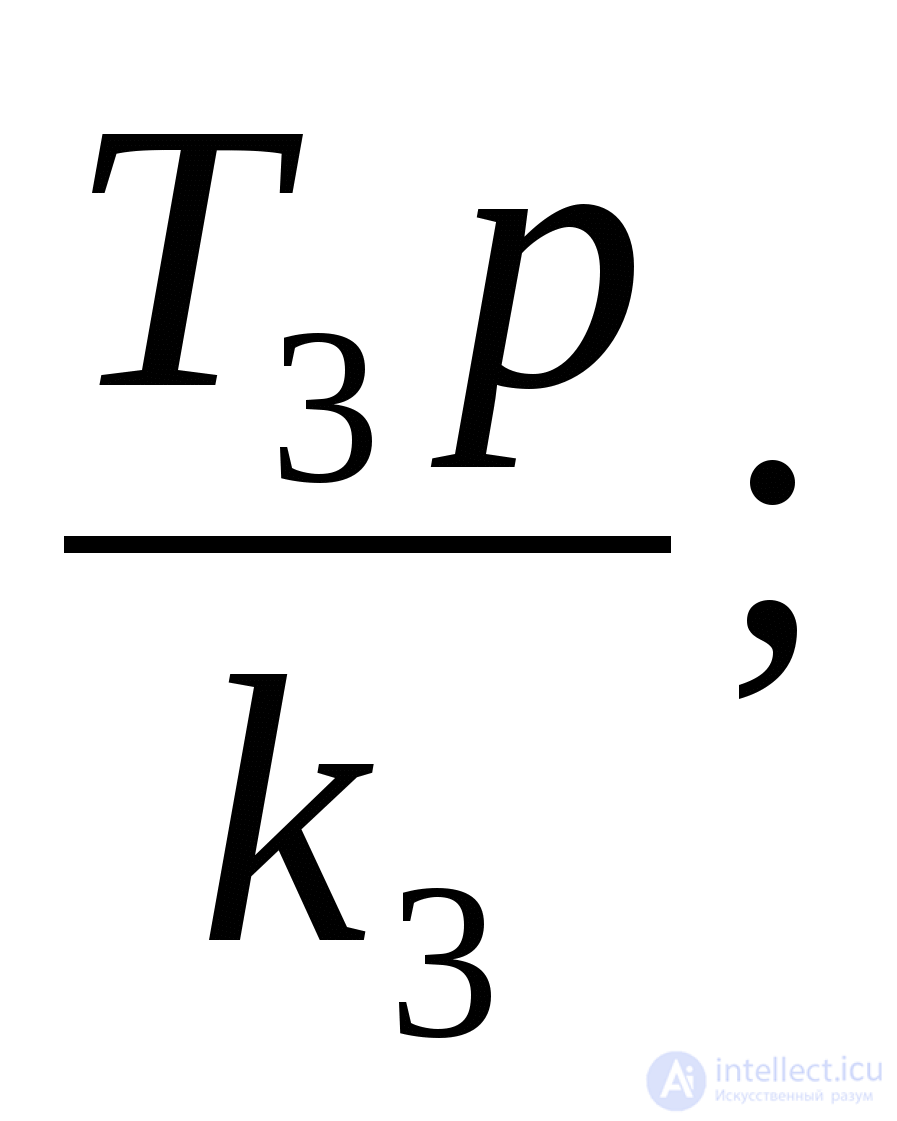 



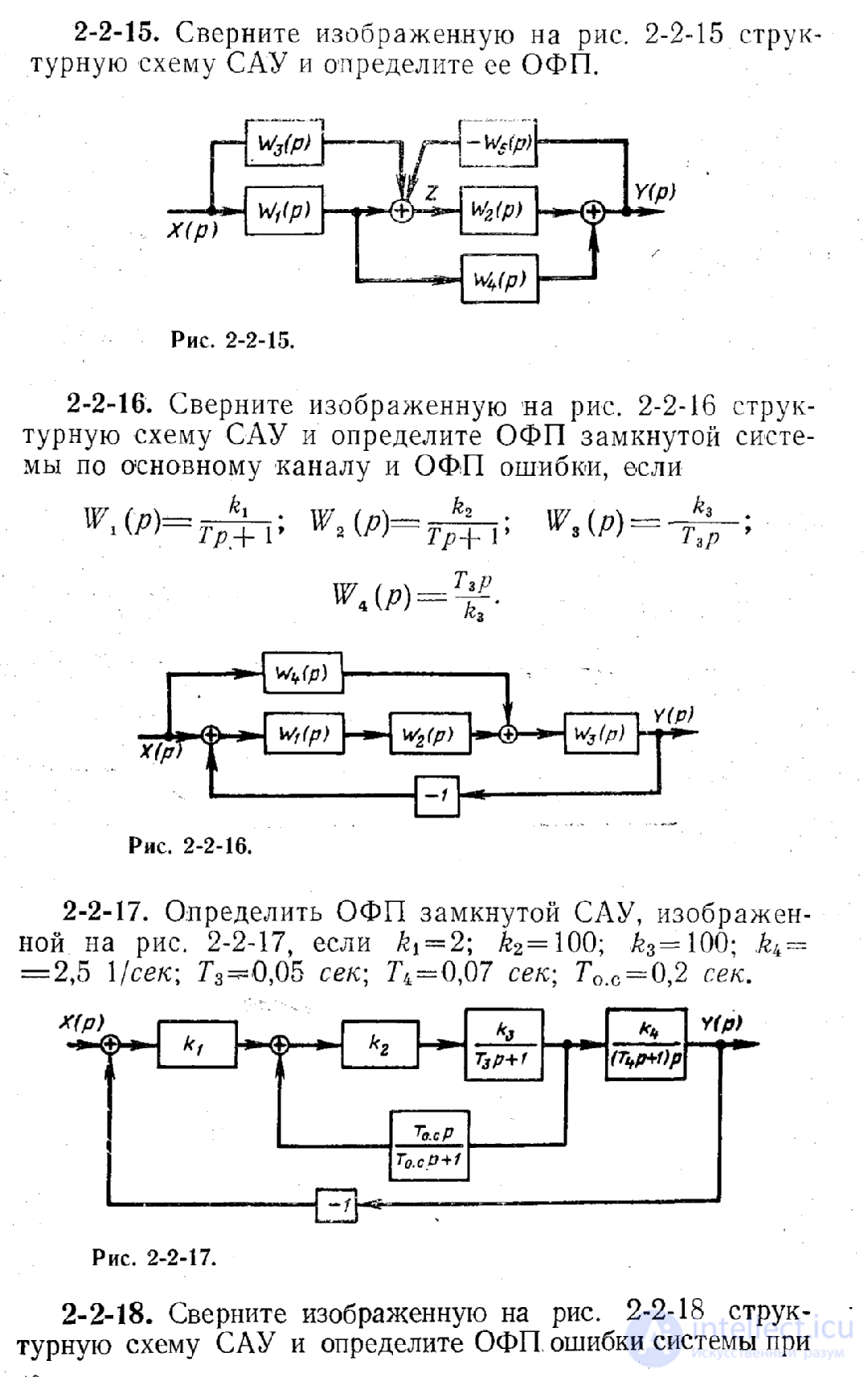
Рисунок 4

Задание 4.

Преобразуя структурную схему (рис. 5), получить в общем виде:

1) передаточную функцию разомкнутой системы;

2) передаточную функцию замкнутой системы для возмущающего воздействия;

3) передаточную функцию замкнутой системы для управляющего воздействия.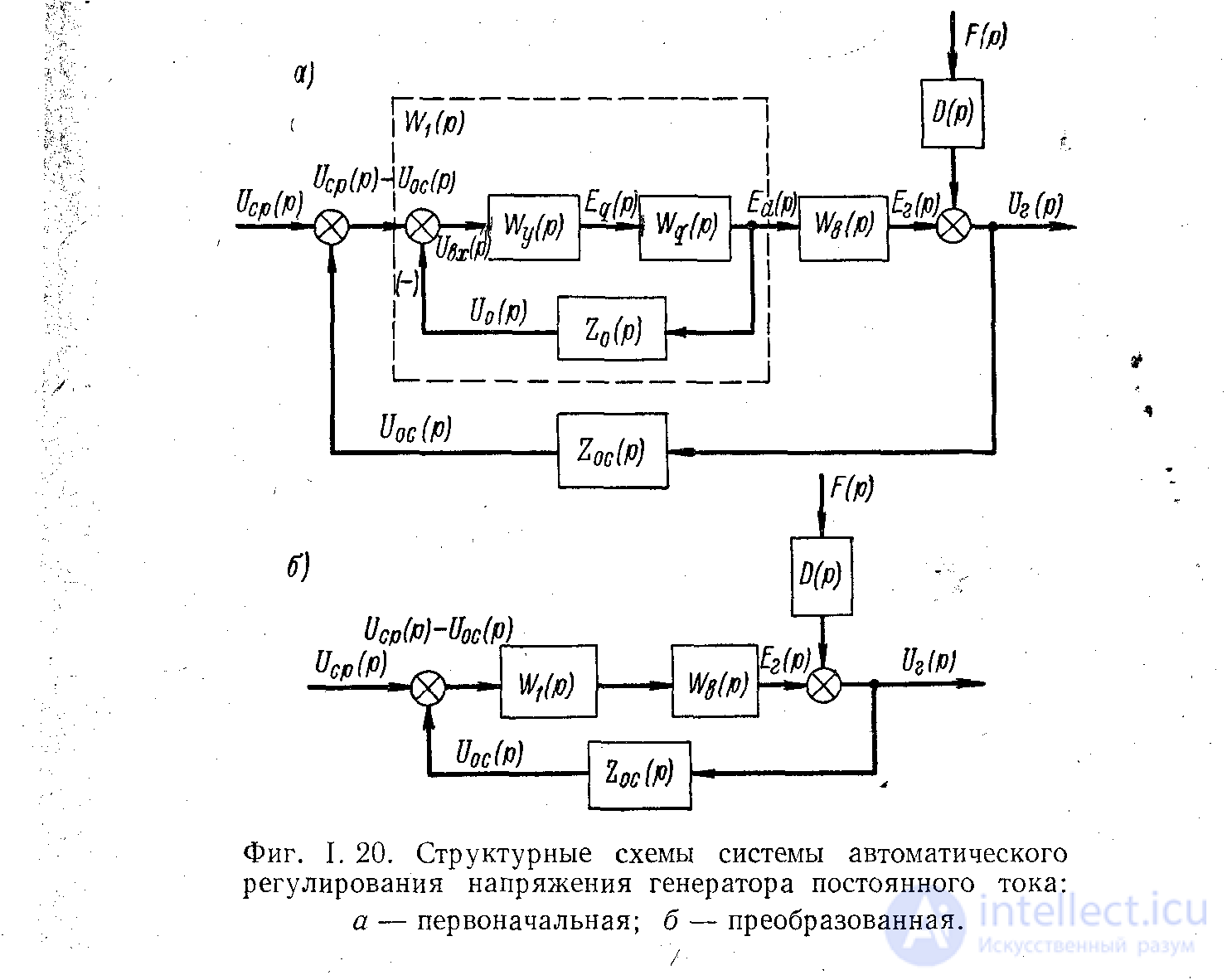



Рисунок 5.
Задание 5.

На основании структурной схемы (рис. 6) получить в общем виде пере-даточные функции системы для выходной величины и ошибки.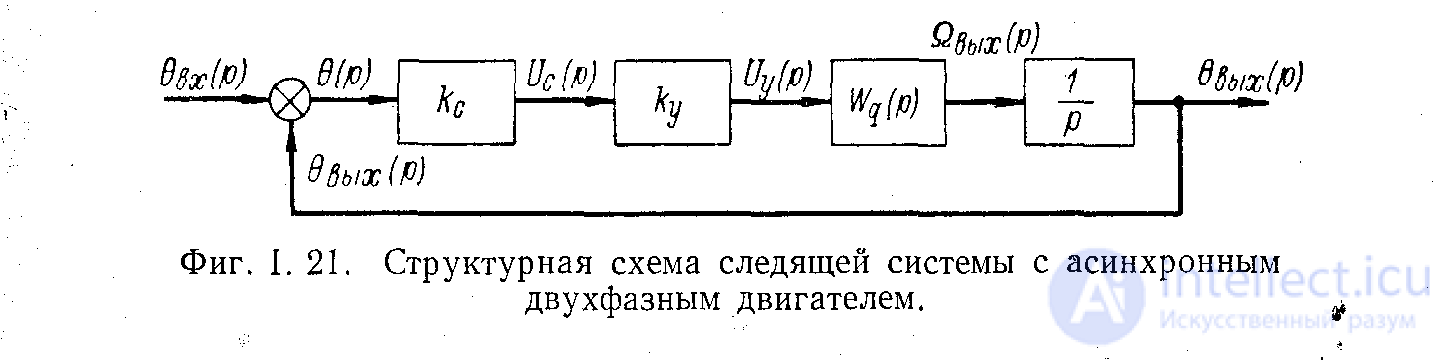



Рисунок 6

Задание 6.

По заданной передаточной функции зарисовать структурную схему системы и граф системы управления по ее структурной схеме.

Задание 7. На основании структурной схемы (рис. 7) получить в общем виде передаточную функцию замкнутой системы. Параметры системы: k_с = 0,4 в/град; Т_g= 0,06 сек.; Т_м= 0,1 сек.; С_е =0,014; j = 297; k_у2 = 5,2, К_у1=1,5, k₀=3,2.



Рисунок 7

Прочтение данной статьи про преобразование структурных схем граф системы управления соответствие структурных схем графам позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое преобразование структурных схем граф системы управления соответствие структурных схем графам и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления